Article contents
Period Lengths for Iterated Functions
Published online by Cambridge University Press: 16 September 2010
Abstract
Let Ωn be the nn-element set consisting of all functions that have {1, 2, 3, . . ., n} as both domain and codomain. Let T(f) be the order of f, i.e., the period of the sequence f, f(2), f(3), f(4) . . . of compositional iterates. A closely related number, B(f) = the product of the lengths of the cycles of f, has previously been used as an approximation for T. This paper proves that the average values of these two quantities are quite different. The expected value of T is
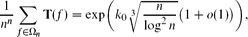 where k0 is a complicated but explicitly defined constant that is approximately 3.36. The expected value of B is much larger:
where k0 is a complicated but explicitly defined constant that is approximately 3.36. The expected value of B is much larger:
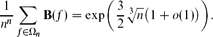
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2010
References
- 3
- Cited by


