Article contents
Partial Shadows of Set Systems
Published online by Cambridge University Press: 20 January 2015
Abstract
The shadow of a system of sets is all sets which can be obtained by taking a set in the original system, and removing a single element. The Kruskal-Katona theorem tells us the minimum possible size of the shadow of 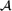 $\mathcal A$, if
$\mathcal A$, if 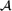 $\mathcal A$ consists of m r-element sets.
$\mathcal A$ consists of m r-element sets.
In this paper, we ask questions and make conjectures about the minimum possible size of a partial shadow for 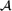 $\mathcal A$, which contains most sets in the shadow of
$\mathcal A$, which contains most sets in the shadow of 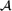 $\mathcal A$. For example, if
$\mathcal A$. For example, if  $\mathcal B$ is a family of sets containing all but one set in the shadow of each set of
$\mathcal B$ is a family of sets containing all but one set in the shadow of each set of 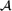 $\mathcal A$, how large must
$\mathcal A$, how large must  $\mathcal B$ be?
$\mathcal B$ be?
MSC classification
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2015
References
- 1
- Cited by


