Packing Loose Hamilton Cycles

Abstract

A subset C of edges in a k-uniform hypergraph H is a loose Hamilton cycle if C covers all the vertices of H and there exists a cyclic ordering of these vertices such that the edges in C are segments of that order and such that every two consecutive edges share exactly one vertex. The binomial random k-uniform hypergraph H^k_n,p has vertex set [n] and an edge set E obtained by adding each k-tuple e ∈ (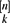$\binom{[n]}{k}$) to E with probability p, independently at random.

Here we consider the problem of finding edge-disjoint loose Hamilton cycles covering all but o(|E|) edges, referred to as the packing problem. While it is known that the threshold probability of the appearance of a loose Hamilton cycle in H^k_n,p is

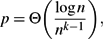$p=\Theta\biggl(\frac{\log n}{n^{k-1}}\biggr),$

the best known bounds for the packing problem are around p = polylog(n)/n. Here we make substantial progress and prove the following asymptotically (up to a polylog(n) factor) best possible result: for p ≥ log^Cn/n^k−1, a random k-uniform hypergraph H^k_n,p with high probability contains

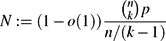$N:=(1-o(1))\frac{\binom{n}{k}p}{n/(k-1)}$

edge-disjoint loose Hamilton cycles.

Our proof utilizes and modifies the idea of ‘online sprinkling’ recently introduced by Vu and the first author.