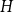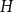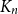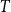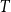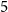1. Introduction
Ramsey’s theorem states that for a fixed graph
![]() $H$
, every 2-edge-colouring of
$H$
, every 2-edge-colouring of
![]() $K_n$
contains a monochromatic copy of
$K_n$
contains a monochromatic copy of
![]() $H$
whenever
$H$
whenever
![]() $n$
is large enough. Perhaps one of the most natural questions extending Ramsey’s theorem is how many monochromatic copies of
$n$
is large enough. Perhaps one of the most natural questions extending Ramsey’s theorem is how many monochromatic copies of
![]() $H$
can be guaranteed to exist. To formalise this question, let the Ramsey multiplicity
$H$
can be guaranteed to exist. To formalise this question, let the Ramsey multiplicity
![]() $M(H;\,n)$
be the minimum number of labelled monochromatic copies of
$M(H;\,n)$
be the minimum number of labelled monochromatic copies of
![]() $H$
over all 2-edge-colourings of
$H$
over all 2-edge-colourings of
![]() $K_n$
. We define the Ramsey multiplicity constant
$K_n$
. We define the Ramsey multiplicity constant
![]() $C(H)$
as
$C(H)$
as
where
![]() $v$
is the number of vertices in
$v$
is the number of vertices in
![]() $H$
. A random 2-edge-coloring of
$H$
. A random 2-edge-coloring of
![]() $K_n$
shows
$K_n$
shows
![]() $C(H)\leq 2^{1-e(H)}$
. We say a graph is common if
$C(H)\leq 2^{1-e(H)}$
. We say a graph is common if
![]() $C(H)=2^{1-e(H)}$
. For example, Goodman’s formula [Reference Goodman13] implies that a triangle is common, i.e.,
$C(H)=2^{1-e(H)}$
. For example, Goodman’s formula [Reference Goodman13] implies that a triangle is common, i.e.,
![]() $C(K_3)=1/4$
.
$C(K_3)=1/4$
.
In 1962, Erdős [Reference Erdős8] conjectured that every complete graph
![]() $K_t$
is common. This was later generalised by Burr and Rosta [Reference Burr and Rosta4], who conjectured that in fact every graph
$K_t$
is common. This was later generalised by Burr and Rosta [Reference Burr and Rosta4], who conjectured that in fact every graph
![]() $H$
is common. In the late 1980s, both conjectures were disproved. Sidorenko [Reference Sidorenko25] proved that a triangle plus a pendant edge is an uncommon graph, and Thomason [Reference Thomason30] proved that
$H$
is common. In the late 1980s, both conjectures were disproved. Sidorenko [Reference Sidorenko25] proved that a triangle plus a pendant edge is an uncommon graph, and Thomason [Reference Thomason30] proved that
![]() $K_t$
is uncommon for
$K_t$
is uncommon for
![]() $t\geq 4$
.
$t\geq 4$
.
Since then more examples of uncommon graphs have been found. For instance, Jagger, Šťovíček and Thomason [Reference Jagger, Šťovíček and Thomason16] proved that every graph containing
![]() $K_4$
as a subgraph is uncommon, and Fox [Reference Fox11] proved that
$K_4$
as a subgraph is uncommon, and Fox [Reference Fox11] proved that
![]() $C(H)$
can be exponentially smaller than the commonality bound
$C(H)$
can be exponentially smaller than the commonality bound
![]() $2^{1-e(H)}$
.
$2^{1-e(H)}$
.
Despite many results on the topic, the full classification of common graphs is still a wide open problem. All known examples of bipartite common graphs connect with progress on Sidorenko’s conjecture [Reference Sidorenko26], since the conjecture implies that every bipartite graph is common. The converse is also an open question — does every bipartite common graph satisfies Sidorenko’s conjecture? Very recently it was shown [Reference Kráľ, Noel, Norin, Volec and Wei17] that a bipartite graph satisfies Sidorenko’s conjecture if and only if it is common in any multi-colour sense. There has been some progress on Sidorenko’s conjecture (see, for example, [Reference Conlon and Lee7] and references therein) but the full conjecture remains open.
There are not many non-bipartite graphs known to be common. For example, one of the earliest applications of the flag algebra method established that the 5-wheel is common [Reference Hatami, Hladký, Norine, Razborov and Král’15]. In case of tripartite graphs, a few more examples have been collected, e.g., odd cycles [Reference Sidorenko25] and even wheels [Reference Jagger, Šťovíček and Thomason16, Reference Sidorenko27].
Two examples of general classes of non-bipartite common graphs are triangle-vertex-trees and triangle-edge-trees, obtained by Sidorenko [Reference Sidorenko27] and reproved by Jagger, Šťovíček, and Thomason [Reference Jagger, Šťovíček and Thomason16]. These can be described recursively. A single triangle is a triangle-tree and one may obtain a triangle tree by identifying a single vertex or an edge of a new triangle with a vertex or an edge, respectively, in a triangle tree. A triangle tree is a triangle-vertex-tree (resp. triangle-edge-tree) if it is obtained by identifying only vertices (resp. edges). See Figure 1 for examples.

Figure 1. Examples of a triangle vertex tree, triangle edge tree, and triangle tree.
Jagger, Šťovíček, and Thomason [Reference Jagger, Šťovíček and Thomason16] asked whether tree-like structures other than triangle-vertex (or triangle-edge) trees formed from triangles are common. In particular, they asked if the triangle-tree formed by three triangles, as described in Figure 2, is common. We ultimately answer these questions.

Figure 2. A triangle tree suggested by Jagger, Šťovíček, and Thomason [Reference Jagger, Šťovíček and Thomason16].
Theorem 1.1. Every triangle-tree is common.
Non-bipartite graphs are more likely to be uncommon than bipartite graphs in many ways. Firstly, no examples of bipartite uncommon graphs, which would disprove Sidorenko’s conjecture, are known. Additionally, Fox [Reference Fox11, Lemma 2.1] observed that any graph with chromatic number at least four and small enough average degree is always uncommon. And most importantly, there is a well-known strategy [Reference Jagger, Šťovíček and Thomason16, Theorem 4] to produce non-bipartite uncommon graphs. That is, by adding a (possibly large) pendant tree, e.g., a long path, to a non-bipartite graph. Sidorenko’s counterexample, the triangle plus a pendant edge, for the Burr–Rosta conjecture can be seen as one of the earliest examples of this kind.
Our second result states that for some tripartite graphs this strategy of adding a pendant tree fails when adding a small pendant tree. In other words, there are tripartite graphs that are ‘robustly common’ in the sense that adding any tree of bounded size does not break their commonality. For a tree
![]() $T$
and a graph
$T$
and a graph
![]() $H$
, let
$H$
, let
![]() $T*_{u}^{v}H$
be the graph obtained by identifying
$T*_{u}^{v}H$
be the graph obtained by identifying
![]() $u\in V(T)$
and
$u\in V(T)$
and
![]() $v\in V(H)$
.
$v\in V(H)$
.
Theorem 1.2. Let
![]() $t$
be a positive integer. If
$t$
be a positive integer. If
![]() $H$
is a triangle-tree with
$H$
is a triangle-tree with
![]() $2e(H)-3v(H)+3 \geq t$
then
$2e(H)-3v(H)+3 \geq t$
then
![]() $T*_{u}^{v}H$
is common for every choice of tree
$T*_{u}^{v}H$
is common for every choice of tree
![]() $T$
with
$T$
with
![]() $e(T)\leq t$
,
$e(T)\leq t$
,
![]() $u\in V(T)$
, and
$u\in V(T)$
, and
![]() $v\in V(H)$
.
$v\in V(H)$
.
Julia Wolf, during her plenary talk at the Canadian Discrete and Algorithmic Mathematics Conference in 2017 on the results from [Reference Saad and Wolf24], prompted to complete the list of connected common graphs on five vertices; Figure 3 depicts the four graphs that had an unknown status at the time of her talk.

Figure 3. Wolf’s list of
![]() $5$
-vertex connected graphs that were not known to be (un)common in 2017.
$5$
-vertex connected graphs that were not known to be (un)common in 2017.
Theorem 1.2 proves that
![]() $H_1$
and
$H_1$
and
![]() $H_2$
are common. The graph
$H_2$
are common. The graph
![]() $H_3$
was proven to be common in an RSI project at MIT [Reference Raghuvanshi21] using flag algebras. Another flag algebra application shows that
$H_3$
was proven to be common in an RSI project at MIT [Reference Raghuvanshi21] using flag algebras. Another flag algebra application shows that
![]() $H_4$
is common; in the Appendix, we give a proof that both
$H_4$
is common; in the Appendix, we give a proof that both
![]() $H_3$
and
$H_3$
and
![]() $H_4$
are common. This completely resolves Wolf’s question.
$H_4$
are common. This completely resolves Wolf’s question.
Analogous applications of flag algebras allow us to show that also various
![]() $4$
-chromatic graphs are common. Specifically, we prove that the
$4$
-chromatic graphs are common. Specifically, we prove that the
![]() $7$
-wheel as well as all the connected
$7$
-wheel as well as all the connected
![]() $7$
-vertex
$7$
-vertex
![]() $K_4$
-free non-
$K_4$
-free non-
![]() $3$
-colourable graphs are common; see Figure 4 for their complete list. Note that the only previously known examples of non-
$3$
-colourable graphs are common; see Figure 4 for their complete list. Note that the only previously known examples of non-
![]() $3$
-colorable graphs were the
$3$
-colorable graphs were the
![]() $5$
-wheel or graphs constructed from gluing copies of the
$5$
-wheel or graphs constructed from gluing copies of the
![]() $5$
-wheel. We suspect that all the odd wheels except
$5$
-wheel. We suspect that all the odd wheels except
![]() $K_4$
are common, although the plain flag algebra approach for the
$K_4$
are common, although the plain flag algebra approach for the
![]() $9$
-wheel is already beyond our computational capacity.
$9$
-wheel is already beyond our computational capacity.

Figure 4. The
![]() $7$
-wheel and all connected non-
$7$
-wheel and all connected non-
![]() $3$
-colourable common graphs on 7 vertices.
$3$
-colourable common graphs on 7 vertices.
Another interesting class of tripartite common graphs was obtained by Sidorenko [Reference Sidorenko27]. If a connected bipartite graph
![]() $H$
satisfies Sidorenko’s conjecture, then adding an apex vertex
$H$
satisfies Sidorenko’s conjecture, then adding an apex vertex
![]() $v$
, i.e., adding all the edges between the new vertex
$v$
, i.e., adding all the edges between the new vertex
![]() $v$
and each vertex of
$v$
and each vertex of
![]() $H$
, gives a tripartite common graph. We conjecture that adding more apex vertices still produces common graphs. For a graph
$H$
, gives a tripartite common graph. We conjecture that adding more apex vertices still produces common graphs. For a graph
![]() $H$
and a positive integer
$H$
and a positive integer
![]() $a$
, let
$a$
, let
![]() $H^{+a}$
be the graph obtained from
$H^{+a}$
be the graph obtained from
![]() $H$
by adding
$H$
by adding
![]() $a$
additional vertices, each new vertex fully connected to
$a$
additional vertices, each new vertex fully connected to
![]() $H$
and not connected to any other new vertex.
$H$
and not connected to any other new vertex.
Conjecture 1.3. If a connected bipartite graph
![]() $H$
satisfies Sidorenko’s conjecture, then for every positive integer
$H$
satisfies Sidorenko’s conjecture, then for every positive integer
![]() $a$
the graph
$a$
the graph
![]() $H^{+a}$
is common. In particular, every complete tripartite graph
$H^{+a}$
is common. In particular, every complete tripartite graph
![]() $K_{r,s,t}$
is common.
$K_{r,s,t}$
is common.
We verify this conjecture for all connected bipartite graphs
![]() $H$
on at most 5 vertices, so, in particular, the complete tripartite graphs
$H$
on at most 5 vertices, so, in particular, the complete tripartite graphs
![]() $K_{2,2,a}$
and
$K_{2,2,a}$
and
![]() $K_{2,3,a}$
are common for every
$K_{2,3,a}$
are common for every
![]() $a\geq 1$
.
$a\geq 1$
.
Theorem 1.4. For every connected bipartite graph
![]() $H$
on at most
$H$
on at most
![]() $5$
vertices and positive integer
$5$
vertices and positive integer
![]() $a$
the graph
$a$
the graph
![]() $H^{+a}$
is common.
$H^{+a}$
is common.
The proof of Theorem 1.4 relies on the computer-assisted flag algebra method, but we also give a computer-free proof for some cases. In particular, we prove without using computers that the octahedron graph, i.e.,
![]() $C_4^{+2}=K_{2,2,2}$
, is common, and generalise it to the so-called beachball graphs
$C_4^{+2}=K_{2,2,2}$
, is common, and generalise it to the so-called beachball graphs
![]() $C_{2k}^{+2}$
for every
$C_{2k}^{+2}$
for every
![]() $k\geq 2$
(see Theorem 4.3).
$k\geq 2$
(see Theorem 4.3).
2. Preliminaries
A graph homomorphism from a graph
![]() $H$
to a graph
$H$
to a graph
![]() $G$
is a vertex map that preserves adjacency. Let
$G$
is a vertex map that preserves adjacency. Let
![]() $\mathrm{Hom}(H,G)$
denote the set of all homomorphisms from
$\mathrm{Hom}(H,G)$
denote the set of all homomorphisms from
![]() $H$
to
$H$
to
![]() $G$
and let
$G$
and let
![]() $t_{H}(G)$
be the probability that a uniform random mapping from
$t_{H}(G)$
be the probability that a uniform random mapping from
![]() $H$
to
$H$
to
![]() $G$
is a homomorphism. i.e.,
$G$
is a homomorphism. i.e.,
![]() $t_{H}(G)=\frac{|\mathrm{Hom}(H,G)|}{v(G)^{v(H)}}$
.
$t_{H}(G)=\frac{|\mathrm{Hom}(H,G)|}{v(G)^{v(H)}}$
.
The graph homomorphism density
![]() $t_H(G)$
naturally extends to weighted graphs and their limit object graphons, i.e., measurable symmetric functions
$t_H(G)$
naturally extends to weighted graphs and their limit object graphons, i.e., measurable symmetric functions
![]() $W\,:\,[0,1]^2\rightarrow [0,1]$
. We define
$W\,:\,[0,1]^2\rightarrow [0,1]$
. We define
 \begin{align*} t_H(W) \,:\!=\, \mathbb{E}\!\left( \prod _{uv \in E(H)} W(x_u,x_v) \right ), \end{align*}
\begin{align*} t_H(W) \,:\!=\, \mathbb{E}\!\left( \prod _{uv \in E(H)} W(x_u,x_v) \right ), \end{align*}
where
![]() $\mathbb{E}$
denotes the integration with respect to the Lebesgue measure on
$\mathbb{E}$
denotes the integration with respect to the Lebesgue measure on
![]() $[0,1]^{v(H)}$
. One may see that the original definition of
$[0,1]^{v(H)}$
. One may see that the original definition of
![]() $t_H(G)$
corresponds to the case
$t_H(G)$
corresponds to the case
![]() $W=W_G$
, where
$W=W_G$
, where
![]() $W_G$
is the block 0-1 graphon constructed by the adjacency matrix of
$W_G$
is the block 0-1 graphon constructed by the adjacency matrix of
![]() $G$
. As nonnegativity of
$G$
. As nonnegativity of
![]() $W$
is unnecessary for the definition, we shall also use
$W$
is unnecessary for the definition, we shall also use
![]() $t_H(U)\,:\!=\, \mathbb{E}\!\left( \prod _{uv \in E(H)} U(x_u,x_v) \right )$
for signed graphons
$t_H(U)\,:\!=\, \mathbb{E}\!\left( \prod _{uv \in E(H)} U(x_u,x_v) \right )$
for signed graphons
![]() $U$
, i.e., measurable symmetric functions
$U$
, i.e., measurable symmetric functions
![]() $U\,:\, [0,1]^2\rightarrow [{-}1,1]$
.
$U\,:\, [0,1]^2\rightarrow [{-}1,1]$
.
Given a graphon
![]() $W$
, a
$W$
, a
![]() $W$
-random graph of order
$W$
-random graph of order
![]() $n$
is a graph obtained from
$n$
is a graph obtained from
![]() $W$
by sampling
$W$
by sampling
![]() $n$
points from
$n$
points from
![]() $[0,1]$
independently and uniformly at random, associating each point with one of the
$[0,1]$
independently and uniformly at random, associating each point with one of the
![]() $n$
vertices, and joining two vertices
$n$
vertices, and joining two vertices
![]() $x,y \in [0,1]$
by an edge with probability
$x,y \in [0,1]$
by an edge with probability
![]() $W(x,y)$
. It can be proven (see, for example, [Reference Lovász19]) that if
$W(x,y)$
. It can be proven (see, for example, [Reference Lovász19]) that if
![]() $G_n$
is a
$G_n$
is a
![]() $W$
-random graph on
$W$
-random graph on
![]() $n$
vertices, then for every graph
$n$
vertices, then for every graph
![]() $H$
the homomorphism density
$H$
the homomorphism density
![]() $t_H(G_n)$
converges to
$t_H(G_n)$
converges to
![]() $t_H(W)$
with probability one.
$t_H(W)$
with probability one.
The number of monochromatic copies of a graph
![]() $H$
in any 2-edge-colouring of a complete graph can be viewed as the number of copies of
$H$
in any 2-edge-colouring of a complete graph can be viewed as the number of copies of
![]() $H$
in the graph formed by edges in the first colour summed up with the number of copies of
$H$
in the graph formed by edges in the first colour summed up with the number of copies of
![]() $H$
in its complement. Similarly, the density of monochromatic (labelled) copies of
$H$
in its complement. Similarly, the density of monochromatic (labelled) copies of
![]() $H$
in a 2-edge-colouring can be rewritten as
$H$
in a 2-edge-colouring can be rewritten as
Note that
![]() $m_H(W)=m_H(1-W)$
and
$m_H(W)=m_H(1-W)$
and
![]() $C(H)=\min _W m_H(W)$
, where the minimum is taken over all graphons
$C(H)=\min _W m_H(W)$
, where the minimum is taken over all graphons
![]() $W$
. Indeed, the minimum exists by the compactness of the space of graphon under the cut norms and the latter follows from considering the
$W$
. Indeed, the minimum exists by the compactness of the space of graphon under the cut norms and the latter follows from considering the
![]() $W$
-random graphs explained in the previous paragraph. Thus, a graph
$W$
-random graphs explained in the previous paragraph. Thus, a graph
![]() $H$
is common if and only if
$H$
is common if and only if
![]() $m_H(W)\geq 2^{1-e(H)}$
for each graphon
$m_H(W)\geq 2^{1-e(H)}$
for each graphon
![]() $W$
.
$W$
.
Let
![]() $\mathcal{E}(H)$
be the family of subgraphs of
$\mathcal{E}(H)$
be the family of subgraphs of
![]() $H$
with even number of edges and let
$H$
with even number of edges and let
![]() $\mathcal{E}_+(H)$
be the collection of nonempty graphs in
$\mathcal{E}_+(H)$
be the collection of nonempty graphs in
![]() $\mathcal{E}(H)$
. Then, with
$\mathcal{E}(H)$
. Then, with
![]() $U\,:\!=\,2W-1$
,
$U\,:\!=\,2W-1$
,
 \begin{align} m_H(W) &= t_H\!\left(\frac{1+U}{2}\right ) +t_H\!\left(\frac{1-U}{2}\right )\nonumber \\ &=2^{1-e(H)}\sum _{F\in \mathcal{E}(H)} t_F(U) = 2^{1-e(H)}\!\left(1 + \sum _{F\in \mathcal{E}_+(H)}t_F(U)\right ). \end{align}
\begin{align} m_H(W) &= t_H\!\left(\frac{1+U}{2}\right ) +t_H\!\left(\frac{1-U}{2}\right )\nonumber \\ &=2^{1-e(H)}\sum _{F\in \mathcal{E}(H)} t_F(U) = 2^{1-e(H)}\!\left(1 + \sum _{F\in \mathcal{E}_+(H)}t_F(U)\right ). \end{align}
Hence,
![]() $H$
is common if and only if
$H$
is common if and only if
![]() $\sum _{F\in \mathcal{E}_+(H)}t_F(U)\geq 0$
for every signed graphon
$\sum _{F\in \mathcal{E}_+(H)}t_F(U)\geq 0$
for every signed graphon
![]() $U$
.
$U$
.
An immediate consequence of this expansion is a well-known formula by Goodman [Reference Goodman13].
Lemma 2.1 (Goodman’s formula). For every graphon
![]() $W$
,
$W$
,
![]() $m_{K_3}(W)=\frac{3}{2}m_{K_{1,2}}(W)-\frac{1}{2}$
.
$m_{K_3}(W)=\frac{3}{2}m_{K_{1,2}}(W)-\frac{1}{2}$
.
Proof. By (1),
![]() $m_{K_3}(W) = \frac{3}{4}t_{K_{1,2}}(U) +\frac{1}{4}$
and
$m_{K_3}(W) = \frac{3}{4}t_{K_{1,2}}(U) +\frac{1}{4}$
and
![]() $m_{K_{1,2}}(W) = \frac{1}{2}t_{K_{1,2}}(U)+\frac{1}{2}$
.
$m_{K_{1,2}}(W) = \frac{1}{2}t_{K_{1,2}}(U)+\frac{1}{2}$
.
The following is an easy consequence of Hölder’s inequality, which will be repeatedly used.
Lemma 2.2. Let
![]() $H,F$
, and
$H,F$
, and
![]() $J$
be graphs,
$J$
be graphs,
![]() $W$
a graphon, and
$W$
a graphon, and
![]() $k$
and
$k$
and
![]() $\ell$
positive integers with
$\ell$
positive integers with
![]() $\ell \geq k$
. If
$\ell \geq k$
. If
then
Proof. We use Hölder’s inequality of the form
 \begin{align*} \prod _{i=1}^k\int f_i(x)^k dx \geq \left (\int \prod _{i=1}^k f_i(x) dx \right )^k, \end{align*}
\begin{align*} \prod _{i=1}^k\int f_i(x)^k dx \geq \left (\int \prod _{i=1}^k f_i(x) dx \right )^k, \end{align*}
for nonnegative functions
![]() $f_i$
. Let the integration be the sum of two terms. Then
$f_i$
. Let the integration be the sum of two terms. Then
 \begin{align} \prod _{i=1}^{k} \left(a_i^k+b_i^k\right) \geq \left (\prod _{i=1}^{k}a_i +\prod _{j=1}^k b_j\right )^k, \end{align}
\begin{align} \prod _{i=1}^{k} \left(a_i^k+b_i^k\right) \geq \left (\prod _{i=1}^{k}a_i +\prod _{j=1}^k b_j\right )^k, \end{align}
for nonnegative numbers
![]() $a_i$
and
$a_i$
and
![]() $b_j$
, it follows that
$b_j$
, it follows that
 \begin{align*} m_H(W) &= t_H(W)+t_H(1-W) \geq \frac{t_J(W)^\ell }{t_F(W)^{k-1}}+\frac{t_J(1-W)^\ell }{t_F(1-W)^{k-1}}\\ &= \left (\frac{t_J(W)^\ell }{t_F(W)^{k-1}}+\frac{t_J(1-W)^\ell }{t_F(1-W)^{k-1}}\right )\big (t_F(W)+t_F(1-W)\big )^{k-1} m_F(W)^{-k+1}\\ &\geq (2)\!\left(t_J(W)^{\frac{\ell }{k}} +t_J(1-W)^{\frac{\ell }{k}}\right )^{k}m_F(W)^{-k+1}\\ &\geq 2^{k-\ell }\frac{m_J(W)^{\ell }}{m_F(W)^{k-1}}. \end{align*}
\begin{align*} m_H(W) &= t_H(W)+t_H(1-W) \geq \frac{t_J(W)^\ell }{t_F(W)^{k-1}}+\frac{t_J(1-W)^\ell }{t_F(1-W)^{k-1}}\\ &= \left (\frac{t_J(W)^\ell }{t_F(W)^{k-1}}+\frac{t_J(1-W)^\ell }{t_F(1-W)^{k-1}}\right )\big (t_F(W)+t_F(1-W)\big )^{k-1} m_F(W)^{-k+1}\\ &\geq (2)\!\left(t_J(W)^{\frac{\ell }{k}} +t_J(1-W)^{\frac{\ell }{k}}\right )^{k}m_F(W)^{-k+1}\\ &\geq 2^{k-\ell }\frac{m_J(W)^{\ell }}{m_F(W)^{k-1}}. \end{align*}
Indeed, the first inequality is Hölder’s inequality (2) and the second follows from convexity of the function
![]() $f(z)=z^{\ell/k}$
, as
$f(z)=z^{\ell/k}$
, as
![]() $\ell \geq k$
.
$\ell \geq k$
.
For the proof of Theorem 1.2, we take an information-theoretic approach. We state the following fact about entropy without proof and refer the reader to [Reference Alon and Spencer1] for more detailed information on entropy and conditional entropy.
Lemma 2.3. Let
![]() $X$
be a random variable taking values in a set
$X$
be a random variable taking values in a set
![]() $S$
and let
$S$
and let
![]() $\mathbb{H}(X)$
be the entropy of
$\mathbb{H}(X)$
be the entropy of
![]() $X$
. Then
$X$
. Then
![]() $\mathbb{H}(X)\leq \log |S|$
.
$\mathbb{H}(X)\leq \log |S|$
.
3. Triangle trees
To describe triangle trees, it is convenient to use the notion of tree decompositions, introduced by Halin [Reference Halin14] and developed by Robertson and Seymour [Reference Robertson and Seymour23].
Definition 3.1. A tree-decomposition of a graph
![]() $H$
is a pair
$H$
is a pair
![]() $(\mathcal{F}, \mathcal{T})$
consisting of a family
$(\mathcal{F}, \mathcal{T})$
consisting of a family
![]() $\mathcal{F}$
of vertex-subsets of
$\mathcal{F}$
of vertex-subsets of
![]() $H$
and a tree
$H$
and a tree
![]() $\mathcal{T}$
with
$\mathcal{T}$
with
![]() $V(\mathcal{T})=\mathcal{F}$
such that
$V(\mathcal{T})=\mathcal{F}$
such that
-
1.
 $\bigcup _{X\in \mathcal{F}}X=V(H)$
,
$\bigcup _{X\in \mathcal{F}}X=V(H)$
, -
2. for each
 $e \in E(H)$
, there exists a set
$e \in E(H)$
, there exists a set
 $X \in \mathcal{F}$
such that
$X \in \mathcal{F}$
such that
 $X$
contains
$X$
contains
 $e$
, and
$e$
, and -
3. for
 $X,Y,Z\in \mathcal{F}$
,
$X,Y,Z\in \mathcal{F}$
,
 $X\cap Y\subseteq Z$
whenever
$X\cap Y\subseteq Z$
whenever
 $Z$
lies on the path from
$Z$
lies on the path from
 $X$
to
$X$
to
 $Y$
in
$Y$
in
 $\mathcal{T}$
.
$\mathcal{T}$
.
Following [Reference Conlon and Lee6, Reference Lee18], we say that
![]() $H$
is a
$H$
is a
![]() $J$
-tree if and only if there exists a tree decomposition
$J$
-tree if and only if there exists a tree decomposition
![]() $(\mathcal{F},\mathcal{T})$
such that the subgraph
$(\mathcal{F},\mathcal{T})$
such that the subgraph
![]() $H[X]$
of
$H[X]$
of
![]() $H$
induced on
$H$
induced on
![]() $X\in \mathcal{F}$
is isomorphic to
$X\in \mathcal{F}$
is isomorphic to
![]() $J$
and moreover, there is an isomorphism between
$J$
and moreover, there is an isomorphism between
![]() $H[X]$
and
$H[X]$
and
![]() $H[Y]$
that fixes
$H[Y]$
that fixes
![]() $H[X\cap Y]$
whenever
$H[X\cap Y]$
whenever
![]() $XY\in E(\mathcal{T})$
. Such a tree decomposition
$XY\in E(\mathcal{T})$
. Such a tree decomposition
![]() $(\mathcal{F},\mathcal{T})$
of
$(\mathcal{F},\mathcal{T})$
of
![]() $H$
is called a
$H$
is called a
![]() $J$
-decomposition. When
$J$
-decomposition. When
![]() $J=K_3$
, we simply say that
$J=K_3$
, we simply say that
![]() $H$
is a triangle tree with a triangle decomposition
$H$
is a triangle tree with a triangle decomposition
![]() $(\mathcal{F},\mathcal{T})$
. It is straightforward to see that this definition is equivalent to the recursive one given in the introduction.
$(\mathcal{F},\mathcal{T})$
. It is straightforward to see that this definition is equivalent to the recursive one given in the introduction.
For a triangle tree
![]() $H$
with a triangle decomposition
$H$
with a triangle decomposition
![]() $(\mathcal{F},\mathcal{T})$
, one may easily relate
$(\mathcal{F},\mathcal{T})$
, one may easily relate
![]() $|\mathcal{F}|$
to
$|\mathcal{F}|$
to
![]() $v(H)$
and
$v(H)$
and
![]() $e(H)$
. Let
$e(H)$
. Let
![]() $\varphi (H) \,:\!=\, e(H) - v(H) + 1$
and
$\varphi (H) \,:\!=\, e(H) - v(H) + 1$
and
![]() $\kappa (H) \,:\!=\, 2e(H) - 3v(H) + 3$
.
$\kappa (H) \,:\!=\, 2e(H) - 3v(H) + 3$
.
Lemma 3.2. If
![]() $H$
is a triangle-tree with a triangle-decomposition
$H$
is a triangle-tree with a triangle-decomposition
![]() $(\mathcal{F},\mathcal{T})$
, then
$(\mathcal{F},\mathcal{T})$
, then
![]() $|\mathcal{F}|=\varphi (H)$
and the number of edges
$|\mathcal{F}|=\varphi (H)$
and the number of edges
![]() $XY\in E(\mathcal{T})$
such that the subgraph
$XY\in E(\mathcal{T})$
such that the subgraph
![]() $H[X\cap Y]$
is a single edge equals to
$H[X\cap Y]$
is a single edge equals to
![]() $\kappa (H)$
. In particular,
$\kappa (H)$
. In particular,
![]() $\kappa (H) \le \varphi (H) - 1$
for every triangle-tree
$\kappa (H) \le \varphi (H) - 1$
for every triangle-tree
![]() $H$
.
$H$
.
Proof. Let
![]() $k\,:\!=\,k(\mathcal{F})$
be the number of edges
$k\,:\!=\,k(\mathcal{F})$
be the number of edges
![]() $XY\in E(\mathcal{T})$
such that the subgraph
$XY\in E(\mathcal{T})$
such that the subgraph
![]() $H[X\cap Y]$
is an edge. For an edge
$H[X\cap Y]$
is an edge. For an edge
![]() $e\in E(H)$
, let
$e\in E(H)$
, let
![]() $t_e$
be the number of contributions of
$t_e$
be the number of contributions of
![]() $e$
in the sum
$e$
in the sum
![]() $\sum _{X\in \mathcal{F}} e(H[X])$
. That is,
$\sum _{X\in \mathcal{F}} e(H[X])$
. That is,
On the other hand,
![]() $t_e-1$
is equal to the number of edges
$t_e-1$
is equal to the number of edges
![]() $XY\in E(\mathcal{T})$
such that
$XY\in E(\mathcal{T})$
such that
![]() $H[X\cap Y]$
is the single-edge
$H[X\cap Y]$
is the single-edge
![]() $\{e\}$
, which proves
$\{e\}$
, which proves
![]() $e(H)=3|\mathcal{F}|-k$
. Analogously,
$e(H)=3|\mathcal{F}|-k$
. Analogously,
![]() $v(H)=2|\mathcal{F}|+1 - k$
and hence,
$v(H)=2|\mathcal{F}|+1 - k$
and hence,
![]() $|\mathcal{F}|=e(H)-v(H)-1=\varphi (H)$
and
$|\mathcal{F}|=e(H)-v(H)-1=\varphi (H)$
and
![]() $k(\mathcal{F})=2e(H)-3v(H)+3=\kappa (H)$
. Finally,
$k(\mathcal{F})=2e(H)-3v(H)+3=\kappa (H)$
. Finally,
![]() $\kappa (H) = k \le e(\mathcal{T}) = |\mathcal{F}|-1 = \varphi (H) - 1$
.
$\kappa (H) = k \le e(\mathcal{T}) = |\mathcal{F}|-1 = \varphi (H) - 1$
.
The key ingredient in the proof of Theorem 1.1 is the following lemma.
Lemma 3.3 ([Reference Lee18], Theorem 2.7). If
![]() $H$
is a
$H$
is a
![]() $J$
-tree with a
$J$
-tree with a
![]() $J$
-decomposition
$J$
-decomposition
![]() $(\mathcal{F},\mathcal{T})$
and
$(\mathcal{F},\mathcal{T})$
and
![]() $W$
is a graphon with
$W$
is a graphon with
![]() $t_{J}(W) \gt 0$
, then
$t_{J}(W) \gt 0$
, then
Lemma 3.3 is basically just simplifying multiple applications of the Cauchy–Schwarz inequality or Jensen’s inequality. For example,
![]() $K_{1,1,t}$
is a triangle tree, since there is a triangle decomposition
$K_{1,1,t}$
is a triangle tree, since there is a triangle decomposition
![]() $(\mathcal{F},\mathcal{T})$
that consists of
$(\mathcal{F},\mathcal{T})$
that consists of
![]() $|\mathcal{F}|=t$
and the star
$|\mathcal{F}|=t$
and the star
![]() $\mathcal{T}$
on
$\mathcal{T}$
on
![]() $\mathcal{F}$
with
$\mathcal{F}$
with
![]() $t-1$
leaves, where each vertex subset in
$t-1$
leaves, where each vertex subset in
![]() $\mathcal{F}$
induces a triangle; see Figure 5. Thus, Lemma 3.3 gives
$\mathcal{F}$
induces a triangle; see Figure 5. Thus, Lemma 3.3 gives
![]() $t_{K_{1,1,t}}(W)\geq t_{K_3}(W)^{t}/t_{K_2}(G)^{t-1}$
, which also follows from a standard application of Jensen’s inequality.
$t_{K_{1,1,t}}(W)\geq t_{K_3}(W)^{t}/t_{K_2}(G)^{t-1}$
, which also follows from a standard application of Jensen’s inequality.

Figure 5.
![]() $K_{1,1,4}$
and its tree decomposition
$K_{1,1,4}$
and its tree decomposition
![]() $(\mathcal{F},\mathcal{T})$
.
$(\mathcal{F},\mathcal{T})$
.
In order to prove Theorem 1.1, we are going to apply Lemma 3.3 for
![]() $J=K_3$
.
$J=K_3$
.
Corollary 3.4. If
![]() $H$
is a triangle-tree and
$H$
is a triangle-tree and
![]() $W$
is a nonzero graphon, then
$W$
is a nonzero graphon, then
We are now ready to prove Theorem 1.1.
Proof of Theorem 1.1. Let
![]() $H$
be a triangle tree. If
$H$
be a triangle tree. If
![]() $W=1$
or
$W=1$
or
![]() $W=0$
almost everywhere, then
$W=0$
almost everywhere, then
![]() $m_H(W)=1$
. Otherwise, two applications of (4) yields
$m_H(W)=1$
. Otherwise, two applications of (4) yields
Therefore, by Lemma 2.2 with
![]() $J=K_3$
,
$J=K_3$
,
![]() $H=K_2$
,
$H=K_2$
,
![]() $\ell =\varphi (H)$
and
$\ell =\varphi (H)$
and
![]() $k=\kappa (H)+1$
, we have
$k=\kappa (H)+1$
, we have
Indeed, the last inequality uses the commonality of a triangle, i.e.,
![]() $m_{K_3}(W) \geq 1/4$
.
$m_{K_3}(W) \geq 1/4$
.
To prove Theorem 1.2, we need a slightly more careful analysis than just a simple application of Lemma 3.3. The main tool is [Reference Lee18, Theorem 2.6], which will be stated shortly. Let
![]() $\mathcal{F}$
be a family of subsets of
$\mathcal{F}$
be a family of subsets of
![]() $[k]\,:\!=\,\{1,2,\dots,k\}$
. A Markov tree on
$[k]\,:\!=\,\{1,2,\dots,k\}$
. A Markov tree on
![]() $[k]$
is a pair
$[k]$
is a pair
![]() $(\mathcal{F},\mathcal{T})$
with
$(\mathcal{F},\mathcal{T})$
with
![]() $\mathcal{T}$
a tree on vertex set
$\mathcal{T}$
a tree on vertex set
![]() $\mathcal{F}$
that satisfies
$\mathcal{F}$
that satisfies
-
1.
 $\bigcup _{F\in \mathcal{F}}F=[k]$
and
$\bigcup _{F\in \mathcal{F}}F=[k]$
and -
2. for
 $A,B,C\in \mathcal{F}$
,
$A,B,C\in \mathcal{F}$
,
 $A\cap B\subseteq C$
whenever
$A\cap B\subseteq C$
whenever
 $C$
lies on the path from
$C$
lies on the path from
 $A$
to
$A$
to
 $B$
in
$B$
in
 $\mathcal{T}$
.
$\mathcal{T}$
.
This is an abstract tree-like structure without the graph structure considered in defining tree decompositions. In particular, a tree decomposition of
![]() $H$
is a Markov tree on
$H$
is a Markov tree on
![]() $V(H)$
. For more detailed explanation, we refer to [Reference Lee18]. Let
$V(H)$
. For more detailed explanation, we refer to [Reference Lee18]. Let
![]() $V$
be a finite set and for each
$V$
be a finite set and for each
![]() $F\in \mathcal{F}$
let
$F\in \mathcal{F}$
let
![]() $\textbf{X}_F=(X_{i;F})_{i\in F}$
be a random vector taking values in
$\textbf{X}_F=(X_{i;F})_{i\in F}$
be a random vector taking values in
![]() $V^{F}$
. The following theorem states that there exist random variables
$V^{F}$
. The following theorem states that there exist random variables
![]() $Y_1,Y_2,\dots,Y_k$
such that, for each
$Y_1,Y_2,\dots,Y_k$
such that, for each
![]() $F\in \mathcal{F}$
, the two random vectors
$F\in \mathcal{F}$
, the two random vectors
![]() $(Y_i)_{i\in F}$
and
$(Y_i)_{i\in F}$
and
![]() $\textbf{X}_{F}$
are identically distributed over
$\textbf{X}_{F}$
are identically distributed over
![]() $V^{F}$
and, moreover, the maximum entropy under such constraints can always be attained.
$V^{F}$
and, moreover, the maximum entropy under such constraints can always be attained.
Lemma 3.5 ([Reference Lee18], Theorem 2.6). Let
![]() $(\mathcal{F},\mathcal{T})$
be a Markov tree on
$(\mathcal{F},\mathcal{T})$
be a Markov tree on
![]() $[k]$
. Let
$[k]$
. Let
![]() $V$
be a finite set and for each
$V$
be a finite set and for each
![]() $F\in \mathcal{F}$
let
$F\in \mathcal{F}$
let
![]() $\textbf{X}_F=(X_{i;F})_{i\in F}$
be a random vector taking values in
$\textbf{X}_F=(X_{i;F})_{i\in F}$
be a random vector taking values in
![]() $V^F$
. If
$V^F$
. If
![]() $\left(X_{i;\,A}\right)_{i\in A\cap B}$
and
$\left(X_{i;\,A}\right)_{i\in A\cap B}$
and
![]() $\left(X_{j;\,B}\right)_{j\in A\cap B}$
are identically distributed whenever
$\left(X_{j;\,B}\right)_{j\in A\cap B}$
are identically distributed whenever
![]() $AB\in E(\mathcal{T})$
, then there exists
$AB\in E(\mathcal{T})$
, then there exists
![]() $\textbf{Y}=\left(Y_1,\dots,Y_k\right)$
with entropy
$\textbf{Y}=\left(Y_1,\dots,Y_k\right)$
with entropy
such that
![]() $(Y_i)_{i\in F}$
and
$(Y_i)_{i\in F}$
and
![]() $\textbf{X}_F$
are identically distributed over
$\textbf{X}_F$
are identically distributed over
![]() $V^{F}$
for all
$V^{F}$
for all
![]() $F\in \mathcal{F}$
.
$F\in \mathcal{F}$
.
An entropy analysis using this lemma give the following corollary. Recall that for a tree
![]() $T$
and a graph
$T$
and a graph
![]() $H$
, we denote by
$H$
, we denote by
![]() $T*_{u}^{v}H$
the graph obtained by identifying
$T*_{u}^{v}H$
the graph obtained by identifying
![]() $u\in V(T)$
and
$u\in V(T)$
and
![]() $v\in V(H)$
.
$v\in V(H)$
.
Lemma 3.6. If
![]() $H$
is a triangle-tree and
$H$
is a triangle-tree and
![]() $T$
a tree with at most
$T$
a tree with at most
![]() $\kappa (H)$
edges, then
$\kappa (H)$
edges, then
for every
![]() $u\in V(T)$
and
$u\in V(T)$
and
![]() $v\in V(H)$
.
$v\in V(H)$
.
Using this lemma, the proof of Theorem 1.2 is almost identical to that of Theorem 1.1.
Proof of Theorem 1.2. Let
![]() $H$
be a triangle tree such that
$H$
be a triangle tree such that
![]() $\kappa (H) \ge t$
,
$\kappa (H) \ge t$
,
![]() $T$
a tree with at most
$T$
a tree with at most
![]() $t$
edges, and
$t$
edges, and
![]() $W$
a nonzero graphon. By Lemma 3.2,
$W$
a nonzero graphon. By Lemma 3.2,
![]() $e(H)=3\varphi (H)-\kappa (H)$
and thus,
$e(H)=3\varphi (H)-\kappa (H)$
and thus,
Combining (6) and Lemma 2.2 for
![]() $J=K_3$
,
$J=K_3$
,
![]() $H=K_2$
,
$H=K_2$
,
![]() $\ell =\varphi (H)$
and
$\ell =\varphi (H)$
and
![]() $k=\kappa (H)-e(T)+1$
yields
$k=\kappa (H)-e(T)+1$
yields
Note that in order to apply Lemma 2.2, we required
![]() $\kappa (H) \ge e(T)$
. As
$\kappa (H) \ge e(T)$
. As
![]() $m_{K_3}(W)\geq 1/4$
, we have
$m_{K_3}(W)\geq 1/4$
, we have
Therefore,
![]() $T*_{u}^{v}H$
is common.
$T*_{u}^{v}H$
is common.
It remains to prove Lemma 3.6.
Proof of Lemma 3.6. Let
![]() $(\mathcal{F},\mathcal{T})$
be a triangle decomposition of
$(\mathcal{F},\mathcal{T})$
be a triangle decomposition of
![]() $H$
and
$H$
and
![]() $k\,:\!=\,\kappa (H)$
. Recall that
$k\,:\!=\,\kappa (H)$
. Recall that
![]() $k$
is the number of edges
$k$
is the number of edges
![]() $XY \in E(\mathcal{T})$
such that the subgraph
$XY \in E(\mathcal{T})$
such that the subgraph
![]() $H[X \cap Y] \cong K_2$
. The first step is to find a natural tree decomposition of
$H[X \cap Y] \cong K_2$
. The first step is to find a natural tree decomposition of
![]() $T*_{u}^{v}H$
that extends
$T*_{u}^{v}H$
that extends
![]() $(\mathcal{F},\mathcal{T})$
.
$(\mathcal{F},\mathcal{T})$
.
Let
![]() $T$
be rooted at a leaf
$T$
be rooted at a leaf
![]() $x\in V(T)$
and suppose that we orient each edge of
$x\in V(T)$
and suppose that we orient each edge of
![]() $T$
away from the root. Let
$T$
away from the root. Let
![]() $\mathcal{S}$
be a tree on
$\mathcal{S}$
be a tree on
![]() $E(T)$
, where the oriented edges
$E(T)$
, where the oriented edges
![]() $(u_1,v_1)$
and
$(u_1,v_1)$
and
![]() $(u_2,v_2)$
are adjacent if and only if
$(u_2,v_2)$
are adjacent if and only if
![]() $v_1=u_2$
. One may easily check that
$v_1=u_2$
. One may easily check that
![]() $(E(T),\mathcal{S})$
is a tree decomposition of
$(E(T),\mathcal{S})$
is a tree decomposition of
![]() $T$
. Now pick an edge
$T$
. Now pick an edge
![]() $uu^{\prime}\in E(T)$
, which is a vertex of
$uu^{\prime}\in E(T)$
, which is a vertex of
![]() $\mathcal{S}$
, and connect it to a vertex bag
$\mathcal{S}$
, and connect it to a vertex bag
![]() $X\in \mathcal{F}$
that contains
$X\in \mathcal{F}$
that contains
![]() $v\in V(T)$
while identifying
$v\in V(T)$
while identifying
![]() $u$
and
$u$
and
![]() $v$
. This new tree
$v$
. This new tree
![]() $\mathcal{T}^{\prime}$
, obtained by adding an edge between two vertices
$\mathcal{T}^{\prime}$
, obtained by adding an edge between two vertices
![]() $uu^{\prime}$
and
$uu^{\prime}$
and
![]() $X$
, gives a tree decomposition
$X$
, gives a tree decomposition
![]() $(\mathcal{F}^{\prime},\mathcal{T}^{\prime})$
of
$(\mathcal{F}^{\prime},\mathcal{T}^{\prime})$
of
![]() $T*_{u}^{v}H$
, where
$T*_{u}^{v}H$
, where
![]() $\mathcal{F}^{\prime}\,:\!=\,V(\mathcal{T}^{\prime})=V(\mathcal{T})\cup V(\mathcal{S})$
.
$\mathcal{F}^{\prime}\,:\!=\,V(\mathcal{T}^{\prime})=V(\mathcal{T})\cup V(\mathcal{S})$
.
Since the homomorphic density in a sequence of
![]() $W$
-random graphs of increasing sizes converges to the homomorphic density in
$W$
-random graphs of increasing sizes converges to the homomorphic density in
![]() $W$
, as explained in the preliminaries, it is enough to prove the inequality (6) for an
$W$
, as explained in the preliminaries, it is enough to prove the inequality (6) for an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
instead of a graphon
$G$
instead of a graphon
![]() $W$
. For brevity, we identify the vertex set
$W$
. For brevity, we identify the vertex set
![]() $V\!\left(T*_{u}^{v}H\right)$
with the set
$V\!\left(T*_{u}^{v}H\right)$
with the set
![]() $[t]$
and let
$[t]$
and let
![]() $1\in [t]$
be the vertex shared by
$1\in [t]$
be the vertex shared by
![]() $H$
and
$H$
and
![]() $T$
. For each
$T$
. For each
![]() $F\in \mathcal{F}^{\prime}$
with
$F\in \mathcal{F}^{\prime}$
with
![]() $|F|=3$
, let
$|F|=3$
, let
![]() $\textbf{X}_F=\left(X_{i;\,F}\right)_{i\in F}$
be a uniform random triangle in
$\textbf{X}_F=\left(X_{i;\,F}\right)_{i\in F}$
be a uniform random triangle in
![]() $G$
, labelled by vertices in
$G$
, labelled by vertices in
![]() $F$
. If
$F$
. If
![]() $|F|=2$
then let
$|F|=2$
then let
![]() $\textbf{X}_F=\left(X_{i;\,F}\right)_{i\in F}$
be a random edge labelled by vertices in
$\textbf{X}_F=\left(X_{i;\,F}\right)_{i\in F}$
be a random edge labelled by vertices in
![]() $F$
sampled in such a way that
$F$
sampled in such a way that
![]() $\mathbb{P}[\textbf{X}_{F}=(v_1,v_2)]$
is proportional to the number of triangles that contains the edge
$\mathbb{P}[\textbf{X}_{F}=(v_1,v_2)]$
is proportional to the number of triangles that contains the edge
![]() $v_1v_2\in E(G)$
. We call this possibly non-uniform edge distribution triangle-projected.
$v_1v_2\in E(G)$
. We call this possibly non-uniform edge distribution triangle-projected.
We claim that
![]() $\left(X_{i;\,A}\right)_{i\in A\cap B}$
and
$\left(X_{i;\,A}\right)_{i\in A\cap B}$
and
![]() $(X_{i;\,B})_{i\in A\cap B}$
are identically distributed. If
$(X_{i;\,B})_{i\in A\cap B}$
are identically distributed. If
![]() $|A\cap B|=2$
, then both distributions are triangle-projected. If
$|A\cap B|=2$
, then both distributions are triangle-projected. If
![]() $|A\cap B|=1$
, i.e.,
$|A\cap B|=1$
, i.e.,
![]() $A\cap B=x\in V\!\left(T*_{u}^{v}H\right)$
, then both distributions are proportional to the weighted degree sum
$A\cap B=x\in V\!\left(T*_{u}^{v}H\right)$
, then both distributions are proportional to the weighted degree sum
![]() $\sum _{x\subset e} p_e$
where
$\sum _{x\subset e} p_e$
where
![]() $p_e$
is the probability of an edge being sampled by the triangle-projected distribution. Therefore, by Lemma 3.5, there exists
$p_e$
is the probability of an edge being sampled by the triangle-projected distribution. Therefore, by Lemma 3.5, there exists
![]() $\textbf{Y}=(Y_1,\dots,Y_t)$
with entropy
$\textbf{Y}=(Y_1,\dots,Y_t)$
with entropy
 \begin{align*} &\mathbb{H}(\textbf{Y}) =\sum _{F\in \mathcal{F}^{\prime}}\mathbb{H}(\textbf{X}_F) -\sum _{AB\in E(\mathcal{T}^{\prime})}\mathbb{H}\!\left(\left(X_{i;\,A}\right)_{i\in A\cap B}\right)\\ &=\sum _{F\in \mathcal{F}}\mathbb{H}(\textbf{X}_F) +\sum _{F\in E(T)}\mathbb{H}(\textbf{X}_F) -\sum _{AB\in E(\mathcal{T})}\mathbb{H}\!\left(\left(X_{i;\,A}\right)_{i\in A\cap B}\right) -\sum _{AB\in E(\mathcal{S})}\mathbb{H}\!\left(\left(X_{i;\,A}\right)_{i\in A\cap B}\right) -\mathbb{H}(Y_{1}). \end{align*}
\begin{align*} &\mathbb{H}(\textbf{Y}) =\sum _{F\in \mathcal{F}^{\prime}}\mathbb{H}(\textbf{X}_F) -\sum _{AB\in E(\mathcal{T}^{\prime})}\mathbb{H}\!\left(\left(X_{i;\,A}\right)_{i\in A\cap B}\right)\\ &=\sum _{F\in \mathcal{F}}\mathbb{H}(\textbf{X}_F) +\sum _{F\in E(T)}\mathbb{H}(\textbf{X}_F) -\sum _{AB\in E(\mathcal{T})}\mathbb{H}\!\left(\left(X_{i;\,A}\right)_{i\in A\cap B}\right) -\sum _{AB\in E(\mathcal{S})}\mathbb{H}\!\left(\left(X_{i;\,A}\right)_{i\in A\cap B}\right) -\mathbb{H}(Y_{1}). \end{align*}
Recall that the vertex 1 is the vertex shared by
![]() $T$
and
$T$
and
![]() $H$
, so
$H$
, so
![]() $Y_1$
means the random image of the vertex with respect to
$Y_1$
means the random image of the vertex with respect to
![]() $\textbf{Y}$
. For
$\textbf{Y}$
. For
![]() $F\in \mathcal{F}$
,
$F\in \mathcal{F}$
,
![]() $\mathbb{H}(\textbf{X}_F)=\log |\mathrm{Hom}(K_3,G)|$
, since
$\mathbb{H}(\textbf{X}_F)=\log |\mathrm{Hom}(K_3,G)|$
, since
![]() $\textbf{X}_F$
is a uniform random triangle. For
$\textbf{X}_F$
is a uniform random triangle. For
![]() $F\in E(T)$
,
$F\in E(T)$
,
![]() $\mathbb{H}(\textbf{X}_F)$
is the entropy
$\mathbb{H}(\textbf{X}_F)$
is the entropy
![]() $h_e$
of the triangle-projected edge distribution. There are exactly
$h_e$
of the triangle-projected edge distribution. There are exactly
![]() $k$
cases such that
$k$
cases such that
![]() $|A\cap B|=2$
and
$|A\cap B|=2$
and
![]() $AB\in E(\mathcal{T})$
, and for such cases,
$AB\in E(\mathcal{T})$
, and for such cases,
![]() $\mathbb{H}\!\left(\left(X_{i;\,A}\right)_{i\in A\cap B}\right)=h_e$
. Thus,
$\mathbb{H}\!\left(\left(X_{i;\,A}\right)_{i\in A\cap B}\right)=h_e$
. Thus,
 \begin{align*} \mathbb{H}(\textbf{Y}) &=|\mathcal{F}|\log |\mathrm{Hom}(K_3,G)| + \sum _{F\in E(T)}\mathbb{H}(\textbf{X}_F) -\sum _{AB\in E(\mathcal{T}^{\prime})}\mathbb{H}\!\left(\left(X_{i;\,A}\right)_{i\in A\cap B}\right) \\&\geq |\mathcal{F}|\log |\mathrm{Hom}(K_3,G)| - (k-e(T))h_e - (e(\mathcal{T}^{\prime})-k)\log |V(G)| \\ &\geq |\mathcal{F}|\log |\mathrm{Hom}(K_3,G)| - (k-e(T))\log |\mathrm{Hom}(K_2,G)| - (e(\mathcal{T}^{\prime})-k)\log n. \end{align*}
\begin{align*} \mathbb{H}(\textbf{Y}) &=|\mathcal{F}|\log |\mathrm{Hom}(K_3,G)| + \sum _{F\in E(T)}\mathbb{H}(\textbf{X}_F) -\sum _{AB\in E(\mathcal{T}^{\prime})}\mathbb{H}\!\left(\left(X_{i;\,A}\right)_{i\in A\cap B}\right) \\&\geq |\mathcal{F}|\log |\mathrm{Hom}(K_3,G)| - (k-e(T))h_e - (e(\mathcal{T}^{\prime})-k)\log |V(G)| \\ &\geq |\mathcal{F}|\log |\mathrm{Hom}(K_3,G)| - (k-e(T))\log |\mathrm{Hom}(K_2,G)| - (e(\mathcal{T}^{\prime})-k)\log n. \end{align*}
Indeed, the first inequality follows from the bound
![]() $\mathbb{H}\!\left(\left(X_{i;\,A}\right)_{i\in A\cap B}\right)\leq \log n$
by Lemma 2.3 when
$\mathbb{H}\!\left(\left(X_{i;\,A}\right)_{i\in A\cap B}\right)\leq \log n$
by Lemma 2.3 when
![]() $|A\cap B|=1$
, and the second follows from the bound
$|A\cap B|=1$
, and the second follows from the bound
![]() $h_e\leq \log \left|\mathrm{Hom}\!\left(T*_{u}^{v}H,G\right)\right|$
by the same lemma. Again by Lemma 2.3,
$h_e\leq \log \left|\mathrm{Hom}\!\left(T*_{u}^{v}H,G\right)\right|$
by the same lemma. Again by Lemma 2.3,
![]() $\mathbb{H}(\textbf{Y})\leq \log |\mathrm{Hom}(H,G)|$
. Thus,
$\mathbb{H}(\textbf{Y})\leq \log |\mathrm{Hom}(H,G)|$
. Thus,
 \begin{align*} t_{T*_{u}^{v}H}(G)&= \frac{|\mathrm{Hom}(T*_{u}^{v}H,G)|}{n^{v(H)+v(T)-1}} \geq \frac{|\mathrm{Hom}(K_3,G)|^{|\mathcal{F}|}}{|\mathrm{Hom}(K_2,G)|^{k-e(T)}n^{e(\mathcal{T}^{\prime})-k}}\cdot \frac{1}{n^{v(H)+v(T)-1}}\\ &=\frac{t_{K_3}(G)^{|\mathcal{F}|}}{t_{K_2}(G)^{k-e(T)}n^{e(\mathcal{T}^{\prime})+k-2e(T)}}\cdot \frac{n^{3|\mathcal{F}|}}{n^{v(H)+v(T)-1}} =\frac{t_{K_3}(G)^{|\mathcal{F}|}}{t_{K_2}(G)^{k-e(T)}}, \end{align*}
\begin{align*} t_{T*_{u}^{v}H}(G)&= \frac{|\mathrm{Hom}(T*_{u}^{v}H,G)|}{n^{v(H)+v(T)-1}} \geq \frac{|\mathrm{Hom}(K_3,G)|^{|\mathcal{F}|}}{|\mathrm{Hom}(K_2,G)|^{k-e(T)}n^{e(\mathcal{T}^{\prime})-k}}\cdot \frac{1}{n^{v(H)+v(T)-1}}\\ &=\frac{t_{K_3}(G)^{|\mathcal{F}|}}{t_{K_2}(G)^{k-e(T)}n^{e(\mathcal{T}^{\prime})+k-2e(T)}}\cdot \frac{n^{3|\mathcal{F}|}}{n^{v(H)+v(T)-1}} =\frac{t_{K_3}(G)^{|\mathcal{F}|}}{t_{K_2}(G)^{k-e(T)}}, \end{align*}
where the last equality follows from the identity
![]() $e(\mathcal{T}^{\prime})=e(\mathcal{T})+e(\mathcal{S})+1 = |\mathcal{F}|+e(T)-1$
and Lemma 3.2.
$e(\mathcal{T}^{\prime})=e(\mathcal{T})+e(\mathcal{S})+1 = |\mathcal{F}|+e(T)-1$
and Lemma 3.2.
4. Beachball graphs and bipartite graphs with apex vertices
The proof of Theorem 1.4 combines our novel ideas and the flag algebra method developed by Razborov [Reference Razborov22]. To demonstrate how the new method works without using flag algebras, we firstly prove that
![]() $K_{2,2,2}$
is common.
$K_{2,2,2}$
is common.
Theorem 4.1. The octahedron
![]() $K_{2,2,2}$
is common.
$K_{2,2,2}$
is common.
By a standard application of the Cauchy–Schwarz inequality (or Lemma 3.3), it is easy to see that
![]() $t_{K_{2,2,2}}(W) \geq t_{K_{1,2,2}}(W)^2/t_{C_4}(W)$
. Then by Lemma 2.2, we immediately obtain
$t_{K_{2,2,2}}(W) \geq t_{K_{1,2,2}}(W)^2/t_{C_4}(W)$
. Then by Lemma 2.2, we immediately obtain
By Sidorenko’s theorem [Reference Sidorenko27], the 4-wheel
![]() $K_{1,2,2}$
is common; however,
$K_{1,2,2}$
is common; however,
![]() $m_{C_4}(W)=1/8$
if and only if
$m_{C_4}(W)=1/8$
if and only if
![]() $W=1/2$
almost everywhere, i.e.,
$W=1/2$
almost everywhere, i.e.,
![]() $W$
is quasirandom, the naive approach using commonality of
$W$
is quasirandom, the naive approach using commonality of
![]() $K_{1,2,2}$
while bounding
$K_{1,2,2}$
while bounding
![]() $m_{C_4}$
from above does not work. We circumvent this difficulty by comparing
$m_{C_4}$
from above does not work. We circumvent this difficulty by comparing
![]() $m_{K_{1,2,2}}(W)$
and
$m_{K_{1,2,2}}(W)$
and
![]() $m_{C_4}(W)$
. Another application of the Cauchy–Schwarz inequality, together with Lemma 2.2, gives
$m_{C_4}(W)$
. Another application of the Cauchy–Schwarz inequality, together with Lemma 2.2, gives
For brevity, denote
![]() $D\,:\!=\,K_{1,1,2}$
, which is the diamond graph obtained by adding a diagonal edge to the 4-cycle. The following lemma, partly motivated by [Reference Hatami, Hladký, Norine, Razborov and Král’15], enables us to compare
$D\,:\!=\,K_{1,1,2}$
, which is the diamond graph obtained by adding a diagonal edge to the 4-cycle. The following lemma, partly motivated by [Reference Hatami, Hladký, Norine, Razborov and Král’15], enables us to compare
![]() $m_{D}(W)$
and
$m_{D}(W)$
and
![]() $m_{C_4}(W)$
.
$m_{C_4}(W)$
.
Lemma 4.2. Let
![]() $0\leq c\leq \left(3-\sqrt{5}\right)/4$
. For any graphon
$0\leq c\leq \left(3-\sqrt{5}\right)/4$
. For any graphon
![]() $W$
, the following inequality holds
$W$
, the following inequality holds
Proof. Using (1) with
![]() $U\,:\!=\,2W-1$
and
$U\,:\!=\,2W-1$
and
![]() $H=D$
, we obtain
$H=D$
, we obtain
where
![]() $K_3^+$
denotes the triangle plus a pendant edge. The same argument for
$K_3^+$
denotes the triangle plus a pendant edge. The same argument for
![]() $m_{C_4}(W)$
yields
$m_{C_4}(W)$
yields
and thus,
 \begin{align} m_D(W) - \frac{1}{16} & - c\!\left(m_{C4}(W)-\frac{1}{8}\right)\nonumber \\ &= \frac{1}{16}\!\left((2-4c)t_{2\cdot K_2}(U)+(8-8c) t_{K_{1,2}}(U) +4t_{K_3^+}(U)+(1-2c)t_{C_4}(U)\right). \end{align}
\begin{align} m_D(W) - \frac{1}{16} & - c\!\left(m_{C4}(W)-\frac{1}{8}\right)\nonumber \\ &= \frac{1}{16}\!\left((2-4c)t_{2\cdot K_2}(U)+(8-8c) t_{K_{1,2}}(U) +4t_{K_3^+}(U)+(1-2c)t_{C_4}(U)\right). \end{align}
Recall that
![]() $U=2W-1$
is not necessarily nonnegative, but
$U=2W-1$
is not necessarily nonnegative, but
![]() $t_{K_{1,2}}(U)$
,
$t_{K_{1,2}}(U)$
,
![]() $t_{2\cdot K_2}(U)$
, and
$t_{2\cdot K_2}(U)$
, and
![]() $t_{C_4}(U)$
are always nonnegative, since
$t_{C_4}(U)$
are always nonnegative, since
![]() $t_{K_{1,2}}(U)\geq t_{K_2}(U)^2=t_{2\cdot K_2}(U)$
and
$t_{K_{1,2}}(U)\geq t_{K_2}(U)^2=t_{2\cdot K_2}(U)$
and
![]() $t_{C_4}(U)\geq t_{K_{1,2}}(U)^2$
. The key inequality we shall prove is
$t_{C_4}(U)\geq t_{K_{1,2}}(U)^2$
. The key inequality we shall prove is
Suppose that this is true. Then (8) gives the lower bound
for
![]() $ 16\big (m_D(W) -1/16 - c(m_{C4}(W)-1/8)\big )$
. This is nonnegative whenever
$ 16\big (m_D(W) -1/16 - c(m_{C4}(W)-1/8)\big )$
. This is nonnegative whenever
![]() $(8-8c)(1-2c)\geq 4$
and
$(8-8c)(1-2c)\geq 4$
and
![]() $c\leq 1/2$
. Taking
$c\leq 1/2$
. Taking
![]() $0\leq c\leq \frac{3-\sqrt{5}}{4}$
suffices for this purpose.
$0\leq c\leq \frac{3-\sqrt{5}}{4}$
suffices for this purpose.
It remains to prove (9). Denote
![]() $\nu (x,z)\,:\!=\,\mathbb{E}_{y}U(x,y)U(y,z)$
and
$\nu (x,z)\,:\!=\,\mathbb{E}_{y}U(x,y)U(y,z)$
and
![]() $\mu (z)\,:\!=\,\mathbb{E}_{w}U(z,w)$
. Then
$\mu (z)\,:\!=\,\mathbb{E}_{w}U(z,w)$
. Then
 \begin{align*} |t_{K_3^+}(U)| &= \left |\mathbb{E}\left[ U(x,y)U(y,z)U(z,x)U(z,w)\right]\right | = \left |\mathbb{E}\left[\nu (x,z)U(z,x)\mu (z)\right]\right |\\[4pt] &\leq \left(\mathbb{E}\left[\nu (x,z)^2\right]\right)^{1/2} \left(\mathbb{E}\left[U(z,x)^2\mu (z)^2\right]\right)^{1/2}\\[4pt] &\leq \left(\mathbb{E}\left[\nu (x,z)^2\right]\right)^{1/2} \left(\mathbb{E}\left[\mu (z)^2\right]\right)^{1/2}=\sqrt{t_{K_{1,2}}(U) t_{C_4}(U)}. \end{align*}
\begin{align*} |t_{K_3^+}(U)| &= \left |\mathbb{E}\left[ U(x,y)U(y,z)U(z,x)U(z,w)\right]\right | = \left |\mathbb{E}\left[\nu (x,z)U(z,x)\mu (z)\right]\right |\\[4pt] &\leq \left(\mathbb{E}\left[\nu (x,z)^2\right]\right)^{1/2} \left(\mathbb{E}\left[U(z,x)^2\mu (z)^2\right]\right)^{1/2}\\[4pt] &\leq \left(\mathbb{E}\left[\nu (x,z)^2\right]\right)^{1/2} \left(\mathbb{E}\left[\mu (z)^2\right]\right)^{1/2}=\sqrt{t_{K_{1,2}}(U) t_{C_4}(U)}. \end{align*}
Proof of Theorem 4.1. Recall that repeated applications of Lemma 2.2 yield
By Goodman’s formula (Lemma 2.1),
![]() $m_{K_{1,2}}(W)=\frac{2}{3}m_{K_3}(W)+\frac{1}{3}$
. Together with the inequality
$m_{K_{1,2}}(W)=\frac{2}{3}m_{K_3}(W)+\frac{1}{3}$
. Together with the inequality
![]() $m_{D}(W)\geq m_{K_3}(W)^2$
that follows from Lemma 2.2 and the inequality
$m_{D}(W)\geq m_{K_3}(W)^2$
that follows from Lemma 2.2 and the inequality
![]() $t_D(W)\geq t_{K_3}(W)^2/t_{K_2}(W)$
, we obtain
$t_D(W)\geq t_{K_3}(W)^2/t_{K_2}(W)$
, we obtain
Therefore, by using Lemma 4.2,
 \begin{align*} m_{K_{2,2,2}}(W) \geq \frac{m_{D}(W)^4}{m_{K_{1,2}}(W)^2 m_{C_4}(W)} \geq \frac{c\cdot m_{D}(W)^4}{\left (\frac{2}{3}\sqrt{m_{D}(W)}+\frac{1}{3}\right )^2 \left (m_D(W)-\frac{1}{16}+\frac{c}{8}\right )}. \end{align*}
\begin{align*} m_{K_{2,2,2}}(W) \geq \frac{m_{D}(W)^4}{m_{K_{1,2}}(W)^2 m_{C_4}(W)} \geq \frac{c\cdot m_{D}(W)^4}{\left (\frac{2}{3}\sqrt{m_{D}(W)}+\frac{1}{3}\right )^2 \left (m_D(W)-\frac{1}{16}+\frac{c}{8}\right )}. \end{align*}
This lower bound is a rational function
![]() $h_c$
of
$h_c$
of
![]() $x\,:\!=\,\sqrt{m_D(W)}$
, which simplifies to
$x\,:\!=\,\sqrt{m_D(W)}$
, which simplifies to
We are looking at the range
![]() $x\geq 1/4$
, as
$x\geq 1/4$
, as
![]() $m_{D}(W)\geq 1/16$
by commonality of
$m_{D}(W)\geq 1/16$
by commonality of
![]() $D$
. Taking, for example,
$D$
. Taking, for example,
![]() $c=1/7\lt \frac{3-\sqrt{5}}{4}$
makes the function
$c=1/7\lt \frac{3-\sqrt{5}}{4}$
makes the function
![]() $h_c$
monotone increasing on
$h_c$
monotone increasing on
![]() $x\geq 1/4$
, and thus,
$x\geq 1/4$
, and thus,
![]() $h_c(z)\geq f_c(1/4)=2^{-11}$
. This proves that
$h_c(z)\geq f_c(1/4)=2^{-11}$
. This proves that
![]() $K_{2,2,2}$
is common.
$K_{2,2,2}$
is common.
Let the
![]() $k$
-beachball graph
$k$
-beachball graph
![]() $B_k$
be the graph obtained by gluing two copies of
$B_k$
be the graph obtained by gluing two copies of
![]() $k$
-wheels along the
$k$
-wheels along the
![]() $k$
-cycle. In particular,
$k$
-cycle. In particular,
![]() $K_{2,2,2}$
is the 4-beachball, since it can be obtained by gluing two copies of 4-wheels along a 4-cycle. See Figure 6, where the 4-cycle is marked bold. As a straightforward generalisation of Theorem 4.1, we also prove the following theorem.
$K_{2,2,2}$
is the 4-beachball, since it can be obtained by gluing two copies of 4-wheels along a 4-cycle. See Figure 6, where the 4-cycle is marked bold. As a straightforward generalisation of Theorem 4.1, we also prove the following theorem.

Figure 6. Graphs
![]() $B_4$
,
$B_4$
,
![]() $B_6$
,
$B_6$
,
![]() $D_2$
, and
$D_2$
, and
![]() $D_4$
.
$D_4$
.
Theorem 4.3. For every
![]() $k\geq 2$
, the
$k\geq 2$
, the
![]() $2k$
-beachball
$2k$
-beachball
![]() $B_{2k}$
is common.
$B_{2k}$
is common.
Proof. The proof is essentially the same as Theorem 4.1 despite a slightly general setting. Let
![]() $D_k$
be the graph obtained by adding two apex vertices to a
$D_k$
be the graph obtained by adding two apex vertices to a
![]() $k$
-edge path, i.e., it consists of
$k$
-edge path, i.e., it consists of
![]() $k$
copies of diamonds glued along
$k$
copies of diamonds glued along
![]() $K_{1,2}$
’s centred at the vertices of degree three in a path-like way, as described in Figure 6. In particular,
$K_{1,2}$
’s centred at the vertices of degree three in a path-like way, as described in Figure 6. In particular,
![]() $D_1=D$
and
$D_1=D$
and
![]() $D_2$
is the 4-wheel. Lemma 3.3 then gives
$D_2$
is the 4-wheel. Lemma 3.3 then gives
and thus,
![]() $m_{D_k}(W)\geq m_D(W)^k/m_{K_{1,2}}(W)^{k-1}$
by Lemma 2.2.
$m_{D_k}(W)\geq m_D(W)^k/m_{K_{1,2}}(W)^{k-1}$
by Lemma 2.2.
The
![]() $2k$
-beachball is then obtained by gluing two copies of
$2k$
-beachball is then obtained by gluing two copies of
![]() $D_k$
along the 4-cycle that contains two vertices of degree three. The standard application of the Cauchy–Schwarz inequality (or Lemma 3.3) gives
$D_k$
along the 4-cycle that contains two vertices of degree three. The standard application of the Cauchy–Schwarz inequality (or Lemma 3.3) gives
![]() $t_{B_{2k}}(W)\geq t_{D_k}(W)^2/t_{C_4}(W)$
, and thus,
$t_{B_{2k}}(W)\geq t_{D_k}(W)^2/t_{C_4}(W)$
, and thus,
by Lemma 2.2. Then again by (10) and Lemma 4.2,
 \begin{align*} m_{B_{2k}}(W) \geq \frac{c\cdot m_{D}(W)^{2k}}{\left (\frac{2}{3}\sqrt{m_{D}(W)}+\frac{1}{3}\right )^{2k-2} \left (m_D(W)-\frac{1}{16}+\frac{c}{8}\right )}. \end{align*}
\begin{align*} m_{B_{2k}}(W) \geq \frac{c\cdot m_{D}(W)^{2k}}{\left (\frac{2}{3}\sqrt{m_{D}(W)}+\frac{1}{3}\right )^{2k-2} \left (m_D(W)-\frac{1}{16}+\frac{c}{8}\right )}. \end{align*}
It remains to minimise rational function
of
![]() $x\,:\!=\,\sqrt{m_D(W)}$
subject to
$x\,:\!=\,\sqrt{m_D(W)}$
subject to
![]() $x\geq 1/4$
. Taking
$x\geq 1/4$
. Taking
![]() $c=1/7$
,
$c=1/7$
,
![]() $h_{k,1/7}$
is a positive constant times the function
$h_{k,1/7}$
is a positive constant times the function
![]() $g_k$
, where the derivative
$g_k$
, where the derivative
Thus, it suffices to check
![]() $p_k(x)=112kx^3+(112k-56)x^2-(5k+5)x-5k\gt 0$
on
$p_k(x)=112kx^3+(112k-56)x^2-(5k+5)x-5k\gt 0$
on
![]() $x\geq 1/4$
. Rearranging the terms, we get
$x\geq 1/4$
. Rearranging the terms, we get
![]() $p_k(x) = 112k(x-1/4)^3+(196k-56)(x-1/4)^2+(72k-33)(x-1/4)+(10k-19)/4$
, which is positive for
$p_k(x) = 112k(x-1/4)^3+(196k-56)(x-1/4)^2+(72k-33)(x-1/4)+(10k-19)/4$
, which is positive for
![]() $x\geq 1/4$
and
$x\geq 1/4$
and
![]() $k\geq 2$
. Therefore,
$k\geq 2$
. Therefore,
![]() $h_{k,1/7}(x)$
is minimised when
$h_{k,1/7}(x)$
is minimised when
![]() $x=1/4$
, which implies
$x=1/4$
, which implies
![]() $B_{2k}$
is common.
$B_{2k}$
is common.
We remark that the constant
![]() $c=1/7$
has been judiciously chosen. Indeed, if
$c=1/7$
has been judiciously chosen. Indeed, if
![]() $c$
is too large, then it gets tougher or even impossible to obtain the inequality in Lemma 4.2. Otherwise, if
$c$
is too large, then it gets tougher or even impossible to obtain the inequality in Lemma 4.2. Otherwise, if
![]() $c$
is too small, then the rational function
$c$
is too small, then the rational function
![]() $h_c(x)$
may attain its local minimum at some
$h_c(x)$
may attain its local minimum at some
![]() $x_0\gt 1/4$
and the optimisation does not work. This does happen if one tries to apply the same argument to prove that
$x_0\gt 1/4$
and the optimisation does not work. This does happen if one tries to apply the same argument to prove that
![]() $K_{2,2,t}$
is common for
$K_{2,2,t}$
is common for
![]() $t\gt 2$
.
$t\gt 2$
.
However, flag algebras allow us to prove inequalities that resemble Lemma 4.2 and can be directly applied to (7), which gives tighter bounds than the previous approach does. In particular, the following generalises Lemma 4.2 to any connected bipartite graph on at most
![]() $5$
vertices.
$5$
vertices.
Lemma 4.4. If
![]() $H$
is a connected bipartite graph on at most
$H$
is a connected bipartite graph on at most
![]() $5$
vertices and
$5$
vertices and
![]() $W$
is a graphon, then
$W$
is a graphon, then
Moreover, if
![]() $H\neq K_2$
, then
$H\neq K_2$
, then
![]() $m_{H^{+1}}(W) = 2^{-v(H)} \cdot m_{H}(W)$
if and only if
$m_{H^{+1}}(W) = 2^{-v(H)} \cdot m_{H}(W)$
if and only if
![]() $m_{C_4}(W)=1/8$
.
$m_{C_4}(W)=1/8$
.
Proof. For any of the ten considered graphs, see Figure 7, the proof of (11) is a straightforward flag algebra application. As the proof of (11) for
![]() $H\neq K_2$
uses
$H\neq K_2$
uses
![]() $m_{C_4}(W) \ge 1/8$
, the moreover part follows by complementary slackness.The flag algebra calculations certifying (11) can be downloaded from
http://lidicky.name/pub/common/
.
$m_{C_4}(W) \ge 1/8$
, the moreover part follows by complementary slackness.The flag algebra calculations certifying (11) can be downloaded from
http://lidicky.name/pub/common/
.

Figure 7. The ten connected bipartite graphs on at most 5 vertices from Lemma 4.4.
Given a common graph
![]() $H$
, if the inequality (11) holds then a direct application of Lemma 2.2 yields that
$H$
, if the inequality (11) holds then a direct application of Lemma 2.2 yields that
![]() $H^{+a}$
is common for every positive integer
$H^{+a}$
is common for every positive integer
![]() $a$
. In particular, we are now ready to prove Theorem 1.4.
$a$
. In particular, we are now ready to prove Theorem 1.4.
Proof of Theorem 1.4. Fix an integer
![]() $a\ge 2$
and a graph
$a\ge 2$
and a graph
![]() $H$
. By convexity (or Lemma 3.3), we have
$H$
. By convexity (or Lemma 3.3), we have
Lemma 2.2 then yields that
and thus, by Lemma 4.4, we conclude that
Since
![]() $H$
is common, i.e.,
$H$
is common, i.e.,
![]() $m_{H}(W) \geq 2^{1-e(H)}$
, we have that
$m_{H}(W) \geq 2^{1-e(H)}$
, we have that
![]() $m_{H^{+a}}(W) \geq 2^{1-e(H)-a\cdot v(H)} = 2^{1-e(H^{+a})}$
. In other words, the graph
$m_{H^{+a}}(W) \geq 2^{1-e(H)-a\cdot v(H)} = 2^{1-e(H^{+a})}$
. In other words, the graph
![]() $H^{+a}$
is common.
$H^{+a}$
is common.
5. Concluding remarks
Stability. When a graph
![]() $H$
is known to be common, it is natural to ask a stability question, i.e., whether the random colouring is (asymptotically) the unique minimiser of the number of monochromatic copies of
$H$
is known to be common, it is natural to ask a stability question, i.e., whether the random colouring is (asymptotically) the unique minimiser of the number of monochromatic copies of
![]() $H$
. In other words, is
$H$
. In other words, is
![]() $m_H(W)$
uniquely minimised by
$m_H(W)$
uniquely minimised by
![]() $W=1/2$
almost everywhere? For bipartite graphs, this question connects to the so-called Forcing Conjecture [Reference Conlon, Fox and Sudakov5, Reference Skokan and Thoma28] stating that if
$W=1/2$
almost everywhere? For bipartite graphs, this question connects to the so-called Forcing Conjecture [Reference Conlon, Fox and Sudakov5, Reference Skokan and Thoma28] stating that if
![]() $H$
is bipartite with at least one cycle and
$H$
is bipartite with at least one cycle and
![]() $p \in (0,1)$
, then
$p \in (0,1)$
, then
![]() $W=p$
almost everywhere uniquely minimises the number of copies of
$W=p$
almost everywhere uniquely minimises the number of copies of
![]() $H$
among all graphons of density
$H$
among all graphons of density
![]() $p$
.
$p$
.
For our results, one may check that that the random colouring is the unique minimiser of
![]() $m_H$
whenever
$m_H$
whenever
![]() $H$
is a triangle tree with
$H$
is a triangle tree with
![]() $\kappa (H)\ge 1$
, i.e., a triangle tree that is not a triangle vertex tree. Indeed, as both
$\kappa (H)\ge 1$
, i.e., a triangle tree that is not a triangle vertex tree. Indeed, as both
![]() $W$
and
$W$
and
![]() $1-W$
must be tight for (3), inspecting the proof of [Reference Lee18, Theorem 2.7] yields that any minimiser of
$1-W$
must be tight for (3), inspecting the proof of [Reference Lee18, Theorem 2.7] yields that any minimiser of
![]() $m_H$
must be
$m_H$
must be
![]() $1/2$
-regular and have the ‘correct’ codegrees, i.e.,
$1/2$
-regular and have the ‘correct’ codegrees, i.e.,
![]() $\int W(x,y) \mathrm{d}y=1/2$
and
$\int W(x,y) \mathrm{d}y=1/2$
and
![]() $\int W(x,z)W(z,y)\mathrm{d}z=1/4$
for almost every
$\int W(x,z)W(z,y)\mathrm{d}z=1/4$
for almost every
![]() $x,y\in [0,1]$
, respectively. In particular, Lemma 4.2 and its applications immediately proves that
$x,y\in [0,1]$
, respectively. In particular, Lemma 4.2 and its applications immediately proves that
![]() $K_{1,1,2}$
,
$K_{1,1,2}$
,
![]() $K_{1,2,2}$
, and
$K_{1,2,2}$
, and
![]() $K_{2,2,2}$
has a unique minimiser. On the other hand, there are infinitely many minimisers of
$K_{2,2,2}$
has a unique minimiser. On the other hand, there are infinitely many minimisers of
![]() $m_{K_3}$
. Indeed,
$m_{K_3}$
. Indeed,
![]() $m_{K_3}(W)=1/4$
for every
$m_{K_3}(W)=1/4$
for every
![]() $1/2$
-regular graphon
$1/2$
-regular graphon
![]() $W$
. Analogusly, any
$W$
. Analogusly, any
![]() $1/2$
-regular graphon minimises
$1/2$
-regular graphon minimises
![]() $m_H$
when
$m_H$
when
![]() $H$
is a fixed triangle vertex tree.
$H$
is a fixed triangle vertex tree.
In all the cases covered in Theorem 1.4 except
![]() $H=K_2$
, the ‘moreover’ part of Lemma 4.4 yields that the random colouring is the unique minimiser. When
$H=K_2$
, the ‘moreover’ part of Lemma 4.4 yields that the random colouring is the unique minimiser. When
![]() $H=K_2$
, the graph
$H=K_2$
, the graph
![]() $H^{+a}$
is simply the complete tripartite graph
$H^{+a}$
is simply the complete tripartite graph
![]() $K_{1,1,a}$
. Therefore, the case
$K_{1,1,a}$
. Therefore, the case
![]() $a=1$
corresponds to
$a=1$
corresponds to
![]() $H^{+a}=K_3$
, so every
$H^{+a}=K_3$
, so every
![]() $1/2$
-regular graphon minimises
$1/2$
-regular graphon minimises
![]() $m_{K_3}$
. On the other hand, if
$m_{K_3}$
. On the other hand, if
![]() $a \ge 2$
, then
$a \ge 2$
, then
![]() $H^{+a}$
is a triangle tree with
$H^{+a}$
is a triangle tree with
![]() $\kappa (H^{+a})=a-1$
, hence by the discussion in the previous paragraph,
$\kappa (H^{+a})=a-1$
, hence by the discussion in the previous paragraph,
![]() $m_{H^{+a}}(W)$
is uniquely minimised when
$m_{H^{+a}}(W)$
is uniquely minimised when
![]() $W=1/2$
almost everywhere.
$W=1/2$
almost everywhere.
Theorem 1.1 for odd cycles. It is certainly possible to generalise Theorem 1.1 by replacing triangles by odd cycles. One way is to define
![]() $C_{2k+1}$
-vertex-tree and
$C_{2k+1}$
-vertex-tree and
![]() $C_{2k+1}$
-edge-tree by allowing recursive additions of odd cycles along vertices or edges, respectively. It is then straightforward to check these graphs are common by using 3.3. Furthermore, one may also generalise Theorem 1.1 by allowing both types of vertex and edge additions of odd cycles of length
$C_{2k+1}$
-edge-tree by allowing recursive additions of odd cycles along vertices or edges, respectively. It is then straightforward to check these graphs are common by using 3.3. Furthermore, one may also generalise Theorem 1.1 by allowing both types of vertex and edge additions of odd cycles of length
![]() $2k+1$
; however, it is unclear that one can allow even more general additive operation between odd cycles, e.g., along a multi-edge path. It might be interesting to obtain a full generalisation of Theorem 1.1 along this line to obtain that
$2k+1$
; however, it is unclear that one can allow even more general additive operation between odd cycles, e.g., along a multi-edge path. It might be interesting to obtain a full generalisation of Theorem 1.1 along this line to obtain that
![]() $C_{2k+1}$
-trees are common for every
$C_{2k+1}$
-trees are common for every
![]() $k$
.
$k$
.
Optimal pendant trees. Let
![]() $H$
be a common graph. Then one may ask what is the smallest
$H$
be a common graph. Then one may ask what is the smallest
![]() $T$
that makes
$T$
that makes
![]() $T*_{u}^{v}H$
uncommon. To formalise, let
$T*_{u}^{v}H$
uncommon. To formalise, let
Note that this parameter might not exist for some bipartite graphs
![]() $H$
. Indeed, if
$H$
. Indeed, if
![]() $H$
satisfies Sidorenko’s conjecture, then
$H$
satisfies Sidorenko’s conjecture, then
![]() $T*_{u}^{v}H$
satisfies the conjecture as well. In particular,
$T*_{u}^{v}H$
satisfies the conjecture as well. In particular,
![]() $H$
is common, and we let
$H$
is common, and we let
![]() $\mathrm{UC}(H)=\infty$
. On the other hand, if
$\mathrm{UC}(H)=\infty$
. On the other hand, if
![]() $H$
is a triangle edge tree, then Lemma 3.6 and the proof of Theorem 1.2 yield a lower bound for
$H$
is a triangle edge tree, then Lemma 3.6 and the proof of Theorem 1.2 yield a lower bound for
![]() $\mathrm{UC}(H)$
that is linear in
$\mathrm{UC}(H)$
that is linear in
![]() $e(H)$
. Also, Fox’s result [Reference Fox11] implies that
$e(H)$
. Also, Fox’s result [Reference Fox11] implies that
![]() $\mathrm{UC}(K_{t,t,t})=O(t^2)$
, which is again linear in terms of the number of edges. It would be interesting to see more precise estimates for
$\mathrm{UC}(K_{t,t,t})=O(t^2)$
, which is again linear in terms of the number of edges. It would be interesting to see more precise estimates for
![]() $\mathrm{UC}(H)$
for various non-bipartite graphs
$\mathrm{UC}(H)$
for various non-bipartite graphs
![]() $H$
.
$H$
.
Ramsey multiplicity constant of small graphs. The smallest graph whose Ramsey multiplicity constant is not known is
![]() $K_4$
, and determining the value of
$K_4$
, and determining the value of
![]() $C(K_4)$
is a well-known open problem in extremal combinatorics with no conjectured value. A direct flag algebra calculation using expressions with 9-vertex subgraph densities yields
$C(K_4)$
is a well-known open problem in extremal combinatorics with no conjectured value. A direct flag algebra calculation using expressions with 9-vertex subgraph densities yields
![]() $C(K_4) \geq 1/33.77 \approx 0.0296$
, which is a slight improvement over previously known lower bound
$C(K_4) \geq 1/33.77 \approx 0.0296$
, which is a slight improvement over previously known lower bound
![]() $1/33.9739 \approx 0.0294343$
[Reference Evans, Pulham and Sheehan9, Reference Giraud12, Reference Nieß20, Reference Sperfeld29, Reference Vaughan32, Reference Wolf33]. Unfortunately, there is still a non-negligible gap from the best upper bound
$1/33.9739 \approx 0.0294343$
[Reference Evans, Pulham and Sheehan9, Reference Giraud12, Reference Nieß20, Reference Sperfeld29, Reference Vaughan32, Reference Wolf33]. Unfortunately, there is still a non-negligible gap from the best upper bound
![]() $1/33.0205 \approx 0.030284$
by Even-Zohar and Linial [Reference Even-Zohar and Linial10], who improved an upper bound
$1/33.0205 \approx 0.030284$
by Even-Zohar and Linial [Reference Even-Zohar and Linial10], who improved an upper bound
![]() $1/33.0135$
of Thomason [Reference Thomason30, Reference Thomason31].
$1/33.0135$
of Thomason [Reference Thomason30, Reference Thomason31].
As noted in the introduction, flag algebra method can be used to prove commonality of many small graphs. In Appendix, we give a proof that the graphs
![]() $H_3$
and
$H_3$
and
![]() $H_4$
from Wolf’s list on Figure 3 are common. Although it is possible to fully inspect the presented proof by hand, some of the steps were obtained by using computers. It would still be interesting to find simpler ‘human-friendly’ proofs of the commonality of
$H_4$
from Wolf’s list on Figure 3 are common. Although it is possible to fully inspect the presented proof by hand, some of the steps were obtained by using computers. It would still be interesting to find simpler ‘human-friendly’ proofs of the commonality of
![]() $H_3$
or
$H_3$
or
![]() $H_4$
.
$H_4$
.
Acknowledgements
Part of this work was carried out when the first, second, and third authors met in Seoul for One-day Meeting on Extremal Combinatorics. We would like to thank the organisers of the workshop for their hospitality. The second author is grateful to David Conlon for helpful discussions and comments. We are also grateful to anonymous referees and Steve Butler for helping us to improve the presentation of this paper.
A. Proof of commonality of
 $H_3$
and
$H_3$
and
 $H_4$
$H_4$
We present proofs of the inequalities
![]() $m_{H_3}(W) \ge 2^{-5}$
and
$m_{H_3}(W) \ge 2^{-5}$
and
![]() $m_{H_4}(W) \ge 2^{-6}$
for all graphons
$m_{H_4}(W) \ge 2^{-6}$
for all graphons
![]() $W$
, where
$W$
, where
![]() $H_3$
and
$H_3$
and
![]() $H_4$
are depicted on Figure 3. The proofs were obtained with a computer assistance using libraries CSDP [Reference B.Borchers3] and QSOPT [Reference Applegate, Cook, Dash and Mevenkamp2].
$H_4$
are depicted on Figure 3. The proofs were obtained with a computer assistance using libraries CSDP [Reference B.Borchers3] and QSOPT [Reference Applegate, Cook, Dash and Mevenkamp2].
Firstly, the following three subgraph density expressions will evaluate to a nonnegative number for every graphon
![]() $W$
due to the commonality of the corresponding graphs:
$W$
due to the commonality of the corresponding graphs:
Moreover, each of these expression will be written as a linear combination of
![]() $5$
-vertex induced subgraph densities; recall that
$5$
-vertex induced subgraph densities; recall that
![]() $\tau _H(W)$
, the induced density of
$\tau _H(W)$
, the induced density of
![]() $H$
in
$H$
in
![]() $W$
, is defined as follows:
$W$
, is defined as follows:
 \begin{equation*} \tau _H(W)\,:\!=\,\mathbb {E} \left [ \prod _{ij\in E(H)}W(x_i,x_j)\prod _{ij\notin E(H)} (1-W(x_i,x_j)) \right ]. \end{equation*}
\begin{equation*} \tau _H(W)\,:\!=\,\mathbb {E} \left [ \prod _{ij\in E(H)}W(x_i,x_j)\prod _{ij\notin E(H)} (1-W(x_i,x_j)) \right ]. \end{equation*}
As we aim to exploit the symmetry of the colours in Ramsey multiplicity, we let
![]() $f(\tau _H(W)) \,:\!=\, \tau _H(W) + \tau _{\overline{H}}(W)$
for every graph
$f(\tau _H(W)) \,:\!=\, \tau _H(W) + \tau _{\overline{H}}(W)$
for every graph
![]() $H$
and extend
$H$
and extend
![]() $f$
linearly to formal linear combinations of graphs.
$f$
linearly to formal linear combinations of graphs.
Let
![]() $P_{ab}(W)$
be the probability measure on
$P_{ab}(W)$
be the probability measure on
![]() $[0,1]^2$
which, given a graphon
$[0,1]^2$
which, given a graphon
![]() $W$
, corresponds to a uniformly sampled pair
$W$
, corresponds to a uniformly sampled pair
![]() $(a,b)$
that induces an edge. Let
$(a,b)$
that induces an edge. Let
![]() $T_{\emptyset }(W)$
and
$T_{\emptyset }(W)$
and
![]() $T_{bc}(W)$
be the probability measures on
$T_{bc}(W)$
be the probability measures on
![]() $[0,1]^3$
that correspond to sampling
$[0,1]^3$
that correspond to sampling
![]() $(a,b,c)$
inducing an independent set and a single-edge graph
$(a,b,c)$
inducing an independent set and a single-edge graph
![]() $\{bc\}$
, respectively. We consider the following 13 density expressions represented as sum-of-squares (we note that (6) and (7) were suggested by a computer search):
$\{bc\}$
, respectively. We consider the following 13 density expressions represented as sum-of-squares (we note that (6) and (7) were suggested by a computer search):
 \begin{align*} { (4)} \quad & 10 \cdot f\!\left(\mathbb{E}_{T_{\emptyset }(W)}\left [\left ( \mathbb{P}\left [x \in \textstyle \bigcap _{z\in \{a,b,c\}} N_z \right ] - \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] \right )^2\right ] \right ) , \\[3pt] { (5)} \quad & 10 \cdot f\!\left(\mathbb{E}_{T_{\emptyset }(W)}\left [\left ( 8\cdot \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] - 1 \right )^2\right ] \right ) , \\[3pt] { (6)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [\Big ( 2\cdot \mathbb{P}[x \in N_b \Delta N_c] + 3\cdot \mathbb{P}\left [x \in (N_b\Delta N_c) \setminus N_a \right ] \Big )^2\right ] \right ) , \\[3pt] { (7)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [ \Big ( 2 \cdot \mathbb{P}[x \in N_b \Delta N_c] - 7 \cdot \mathbb{P}\left [x \in (N_b\Delta N_c) \setminus N_a \right ] \Big )^2\right ] \right ) , \\[3pt] { (8)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [ \left ( \mathbb{P}\left [x \in \textstyle \bigcap _{z\in \{a,b,c\}} N_z\right ] - \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] \right )^2 \right ] \right ) ,\\[3pt] { (9)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [ \left ( \mathbb{P}\left [(x \in N_a \setminus \textstyle \bigcup _{z\in \{b,c\}} N_z\right ] - \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] \right )^2 \right ] \right ) ,\\[3pt] {(10)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [ \left ( \mathbb{P}\left [x \in \textstyle \bigcap _{z\in \{b,c\}} N_z \setminus N_a\right ] - \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] \right )^2 \right ] \right ) , \end{align*}
\begin{align*} { (4)} \quad & 10 \cdot f\!\left(\mathbb{E}_{T_{\emptyset }(W)}\left [\left ( \mathbb{P}\left [x \in \textstyle \bigcap _{z\in \{a,b,c\}} N_z \right ] - \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] \right )^2\right ] \right ) , \\[3pt] { (5)} \quad & 10 \cdot f\!\left(\mathbb{E}_{T_{\emptyset }(W)}\left [\left ( 8\cdot \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] - 1 \right )^2\right ] \right ) , \\[3pt] { (6)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [\Big ( 2\cdot \mathbb{P}[x \in N_b \Delta N_c] + 3\cdot \mathbb{P}\left [x \in (N_b\Delta N_c) \setminus N_a \right ] \Big )^2\right ] \right ) , \\[3pt] { (7)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [ \Big ( 2 \cdot \mathbb{P}[x \in N_b \Delta N_c] - 7 \cdot \mathbb{P}\left [x \in (N_b\Delta N_c) \setminus N_a \right ] \Big )^2\right ] \right ) , \\[3pt] { (8)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [ \left ( \mathbb{P}\left [x \in \textstyle \bigcap _{z\in \{a,b,c\}} N_z\right ] - \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] \right )^2 \right ] \right ) ,\\[3pt] { (9)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [ \left ( \mathbb{P}\left [(x \in N_a \setminus \textstyle \bigcup _{z\in \{b,c\}} N_z\right ] - \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] \right )^2 \right ] \right ) ,\\[3pt] {(10)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [ \left ( \mathbb{P}\left [x \in \textstyle \bigcap _{z\in \{b,c\}} N_z \setminus N_a\right ] - \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] \right )^2 \right ] \right ) , \end{align*}
 \begin{align*} { (11)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [ \left ( \mathbb{P}\left [x \in (N_b\Delta N_c) \setminus N_a\right ] - 2\cdot \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] \right )^2 \right ] \right ) , \\[3pt] { (12)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [ \left ( \mathbb{P}\left [x \in (N_b\Delta N_c) \cap N_a\right ] - 2\cdot \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] \right )^2 \right ] \right ) , \\[3pt] { (13)} \quad & 15 \cdot \mathbb{E}_{a\in [0,1]}\left [ \Big ( \big (2\cdot \mathbb{P}[x\in N_y]-1\big ) \cdot \big ( \mathbb{P}\left [x\in N_a \land y \in N_a \right ] - \mathbb{P}\left [x\notin N_a \land y \notin N_a \right ] \big ) \Big )^2 \right ] , \\[3pt] { (14)} \quad & 15 \cdot f\!\left(\mathbb{E}_{P_{ab}(W)}\left [ \left ( \mathbb{P}\left [x \in N_a\right ] - \mathbb{P}\left [x \in N_b\right ] \right )^2 \right ] \right ) , \\[3pt] { (15)} \quad & 15 \cdot \mathbb{E}_{a\in [0,1]}\left [ \left ( 2\cdot \mathbb{P}\left [x\in N_a \land y \in N_a \right ] + 2\cdot \mathbb{P}\left [x\notin N_a \land y \notin N_a \right ] - 1 \right )^2 \right ],\text{ and } \\[3pt] { (16)} \quad & 30 \cdot f\!\left(\mathbb{E}_{P_{ab}(W)}\left [ \mathbb{P}[x \in N_a \cap N_b] \cdot \big (2\cdot \mathbb{P}\left [y \in N_a \Delta N_b\right ] - 1\big )^2 \right ] \right ) , \end{align*}
\begin{align*} { (11)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [ \left ( \mathbb{P}\left [x \in (N_b\Delta N_c) \setminus N_a\right ] - 2\cdot \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] \right )^2 \right ] \right ) , \\[3pt] { (12)} \quad & 30 \cdot f\!\left(\mathbb{E}_{T_{bc}(W)}\left [ \left ( \mathbb{P}\left [x \in (N_b\Delta N_c) \cap N_a\right ] - 2\cdot \mathbb{P}\left [x \notin \textstyle \bigcup _{z\in \{a,b,c\}} N_z\right ] \right )^2 \right ] \right ) , \\[3pt] { (13)} \quad & 15 \cdot \mathbb{E}_{a\in [0,1]}\left [ \Big ( \big (2\cdot \mathbb{P}[x\in N_y]-1\big ) \cdot \big ( \mathbb{P}\left [x\in N_a \land y \in N_a \right ] - \mathbb{P}\left [x\notin N_a \land y \notin N_a \right ] \big ) \Big )^2 \right ] , \\[3pt] { (14)} \quad & 15 \cdot f\!\left(\mathbb{E}_{P_{ab}(W)}\left [ \left ( \mathbb{P}\left [x \in N_a\right ] - \mathbb{P}\left [x \in N_b\right ] \right )^2 \right ] \right ) , \\[3pt] { (15)} \quad & 15 \cdot \mathbb{E}_{a\in [0,1]}\left [ \left ( 2\cdot \mathbb{P}\left [x\in N_a \land y \in N_a \right ] + 2\cdot \mathbb{P}\left [x\notin N_a \land y \notin N_a \right ] - 1 \right )^2 \right ],\text{ and } \\[3pt] { (16)} \quad & 30 \cdot f\!\left(\mathbb{E}_{P_{ab}(W)}\left [ \mathbb{P}[x \in N_a \cap N_b] \cdot \big (2\cdot \mathbb{P}\left [y \in N_a \Delta N_b\right ] - 1\big )^2 \right ] \right ) , \end{align*}
where
![]() $x$
and
$x$
and
![]() $y$
are uniformly sampled vertices of
$y$
are uniformly sampled vertices of
![]() $W$
, and
$W$
, and
![]() $x \in N_{\star }$
abbreviates the event of sampling an edge between
$x \in N_{\star }$
abbreviates the event of sampling an edge between
![]() $x$
and
$x$
and
![]() $\star$
. Clearly, each expression evaluates to a nonnegative number for any
$\star$
. Clearly, each expression evaluates to a nonnegative number for any
![]() $W$
and can be written as a linear combination of
$W$
and can be written as a linear combination of
![]() $5$
-vertex induced subgraph densities.
$5$
-vertex induced subgraph densities.
As there are
![]() $34$
non-isomorphic
$34$
non-isomorphic
![]() $5$
-vertex graphs and two of them are self-complementary, there are exactly
$5$
-vertex graphs and two of them are self-complementary, there are exactly
![]() $18$
non-isomorphic partitions of
$18$
non-isomorphic partitions of
![]() $E(K_5)$
into two parts (see Figure 8). Therefore, we may identify each expression described in the previous paragraph with a vector from
$E(K_5)$
into two parts (see Figure 8). Therefore, we may identify each expression described in the previous paragraph with a vector from
![]() $\mathbb{R}^{18}$
simply by letting its
$\mathbb{R}^{18}$
simply by letting its
![]() $i$
-th coordinate to be the coefficient of the
$i$
-th coordinate to be the coefficient of the
![]() $i$
-th graph in Figure 8 in the corresponding linear combination. We denote these vectors by
$i$
-th graph in Figure 8 in the corresponding linear combination. We denote these vectors by
![]() $w_1, w_2, \dots, w_{16}$
, and let
$w_1, w_2, \dots, w_{16}$
, and let
![]() $M \,:\!=\, \left (w_1 | w_2 | \cdots | w_{16}\right )$
be the corresponding
$M \,:\!=\, \left (w_1 | w_2 | \cdots | w_{16}\right )$
be the corresponding
![]() $18 \times 16$
matrix. Next, let
$18 \times 16$
matrix. Next, let
![]() $v_A$
and
$v_A$
and
![]() $v_B$
be the vectors from
$v_B$
be the vectors from
![]() $\mathbb{R}^{18}$
representing the expressions
$\mathbb{R}^{18}$
representing the expressions
![]() $480\cdot \left (m(H_3) - 2^{-5}\right )$
and
$480\cdot \left (m(H_3) - 2^{-5}\right )$
and
![]() $960\cdot \left (m(H_4) - 2^{-6}\right )$
, respectively. Then
$960\cdot \left (m(H_4) - 2^{-6}\right )$
, respectively. Then
![]() $v_A$
,
$v_A$
,
![]() $v_B$
, and
$v_B$
, and
![]() $M$
are
$M$
are
 \begin{align*} \left (\begin{array}{cccccccccccccccc} 465\\177\\33\\81\\-15\\-15\\17\\1\\-15\\-15\\-15\\-7\\-15\\-15\\-15\\-15\\-15\\-15\\ \end{array}\right ), \left (\begin{array}{cccccccccccccccc} 945\\273\\17\\113\\-15\\-15\\17\\-15\\-15\\-15\\-15\\-15\\-15\\-15\\-15\\-15\\-15\\-15\\ \end{array}\right ), \text{ and } \left (\begin{array}{c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c} 465& 465& 45& 10& 490& 0& 0& 0& 0& 0& 0& 0& 15& 0& 15& 0\\ 177& 177& 21& 1& 7& 0& 0& 3& 3& 3& 12& 12& 3& 0& 3& 3\\ 49& 65& 5& 0& -27& 0& 0& 1& 0& 0& -8& 0& -3& 1& 3& -3\\ 49& 17& 13& 0& 4& 0& 0& 2& -2& 2& 8& 8& 3& -2& -9& 6\\ 9& 9& -3& -1& -28& 75& 12& 0& 0& 0& 3& 0& -3& 3& -9& 6\\ -15& 33& -3& 1& 4& 0& 0& 0& 0& -6& 0& 0& -3& 3& 15& 6\\ 1& -15& 5& 0& 2& 0& 0& 1& -1& 0& 0& 0& 1& -3& -9& 0\\ 1& 1& 1& 0& 3& -25& -4& 0& 0& 0& -3& -4& -1& 0& 3& -5\\ -15& -15& -3& -4& -28& 0& 0& 0& 0& 6& 0& 0& 3& 6& -9& 6\\ -15& -7& -3& 0& 3& 25& 4& -1& 0& -1& 1& 0& 1& 3& 3& -1\\ -7& -15& -3& 0& 2& 24& 5& 0& 0& 0& 0& -3& -1& 0& -9& 0\\ -15& -15& 1& 0& 1& -24& -5& 0& 0& 0& 0& 1& 1& -3& 3& -3\\ -15& -15& -3& 0& 2& -100& -16& 0& 0& 0& 4& 0& -1& 0& 15& 8\\ -15& -15& -3& 1& 1& 0& 0& 0& 3& 0& 0& 0& -3& -3& 3& 9\\ -15& -15& -3& 0& 3& 0& 0& -2& 0& 1& 0& 0& 3& 4& 3& -1\\ -15& -15& -3& 0& 1& -16& 45& 0& 0& 0& 0& 1& -1& -2& 3& 1\\ -15& -15& -3& 0& 2& 40& -40& 0& 0& 0& 0& 0& 1& 1& -9& 0\\ -15& -15& 5& 0& 0& -40& -250& 0& 0& 0& 0& 10& 5& -5& 15& 10\\ \end{array}\right ), \end{align*}
\begin{align*} \left (\begin{array}{cccccccccccccccc} 465\\177\\33\\81\\-15\\-15\\17\\1\\-15\\-15\\-15\\-7\\-15\\-15\\-15\\-15\\-15\\-15\\ \end{array}\right ), \left (\begin{array}{cccccccccccccccc} 945\\273\\17\\113\\-15\\-15\\17\\-15\\-15\\-15\\-15\\-15\\-15\\-15\\-15\\-15\\-15\\-15\\ \end{array}\right ), \text{ and } \left (\begin{array}{c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c@{\hspace*{5pt}}c} 465& 465& 45& 10& 490& 0& 0& 0& 0& 0& 0& 0& 15& 0& 15& 0\\ 177& 177& 21& 1& 7& 0& 0& 3& 3& 3& 12& 12& 3& 0& 3& 3\\ 49& 65& 5& 0& -27& 0& 0& 1& 0& 0& -8& 0& -3& 1& 3& -3\\ 49& 17& 13& 0& 4& 0& 0& 2& -2& 2& 8& 8& 3& -2& -9& 6\\ 9& 9& -3& -1& -28& 75& 12& 0& 0& 0& 3& 0& -3& 3& -9& 6\\ -15& 33& -3& 1& 4& 0& 0& 0& 0& -6& 0& 0& -3& 3& 15& 6\\ 1& -15& 5& 0& 2& 0& 0& 1& -1& 0& 0& 0& 1& -3& -9& 0\\ 1& 1& 1& 0& 3& -25& -4& 0& 0& 0& -3& -4& -1& 0& 3& -5\\ -15& -15& -3& -4& -28& 0& 0& 0& 0& 6& 0& 0& 3& 6& -9& 6\\ -15& -7& -3& 0& 3& 25& 4& -1& 0& -1& 1& 0& 1& 3& 3& -1\\ -7& -15& -3& 0& 2& 24& 5& 0& 0& 0& 0& -3& -1& 0& -9& 0\\ -15& -15& 1& 0& 1& -24& -5& 0& 0& 0& 0& 1& 1& -3& 3& -3\\ -15& -15& -3& 0& 2& -100& -16& 0& 0& 0& 4& 0& -1& 0& 15& 8\\ -15& -15& -3& 1& 1& 0& 0& 0& 3& 0& 0& 0& -3& -3& 3& 9\\ -15& -15& -3& 0& 3& 0& 0& -2& 0& 1& 0& 0& 3& 4& 3& -1\\ -15& -15& -3& 0& 1& -16& 45& 0& 0& 0& 0& 1& -1& -2& 3& 1\\ -15& -15& -3& 0& 2& 40& -40& 0& 0& 0& 0& 0& 1& 1& -9& 0\\ -15& -15& 5& 0& 0& -40& -250& 0& 0& 0& 0& 10& 5& -5& 15& 10\\ \end{array}\right ), \end{align*}
respectively. Let
![]() $M_A$
and
$M_A$
and
![]() $M_B$
be the submatrices of
$M_B$
be the submatrices of
![]() $M$
obtained by deleting the last and the second to last column, respectively. It follows both
$M$
obtained by deleting the last and the second to last column, respectively. It follows both
![]() $M_A$
and
$M_A$
and
![]() $M_B$
have rank
$M_B$
have rank
![]() $15$
and the unique
$15$
and the unique
![]() $x_A$
and
$x_A$
and
![]() $x_B$
that satisfy
$x_B$
that satisfy
![]() $v_A = M_A x_A$
and
$v_A = M_A x_A$
and
![]() $v_B = M_B x_B$
have nonnegative entries, explicitly given as follows:
$v_B = M_B x_B$
have nonnegative entries, explicitly given as follows:
 \begin{align*} & x_A = \frac{1}{133168} \times \begin{pmatrix} 22852\\ 10730\\ 448079\\ 6584\\ 13776\\ 1168352\\ 22852\\ 1351168\\ 9280\\ 513184\\ 43384\\ 7888\\ 172057\\ 329614\\ 45472 \end{pmatrix} & x_B = \frac{1}{13601} \times \begin{pmatrix} 9628\\ 2465\\ 19430\\ 780\\ 2520\\ 56144\\ 9628\\ 133168\\ 19952\\ 19488\\ 14268\\ 6728\\ 71746\\ 14268\\ 18676 \end{pmatrix} \;. \end{align*}
\begin{align*} & x_A = \frac{1}{133168} \times \begin{pmatrix} 22852\\ 10730\\ 448079\\ 6584\\ 13776\\ 1168352\\ 22852\\ 1351168\\ 9280\\ 513184\\ 43384\\ 7888\\ 172057\\ 329614\\ 45472 \end{pmatrix} & x_B = \frac{1}{13601} \times \begin{pmatrix} 9628\\ 2465\\ 19430\\ 780\\ 2520\\ 56144\\ 9628\\ 133168\\ 19952\\ 19488\\ 14268\\ 6728\\ 71746\\ 14268\\ 18676 \end{pmatrix} \;. \end{align*}
Thus,
![]() $m_{H_3}(W)\ge 2^{-5}$
and
$m_{H_3}(W)\ge 2^{-5}$
and
![]() $m_{H_4}(W) \ge 2^{-6}$
for every graphon
$m_{H_4}(W) \ge 2^{-6}$
for every graphon
![]() $W$
.
$W$
.

Figure 8. Non-isomorphic partitions of
![]() $E(K_5)$
into two parts represented by black and white edges.
$E(K_5)$
into two parts represented by black and white edges.