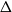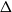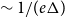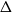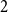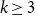1. Introduction
A hypergraph
![]() $G=(V,E)$
is a set of vertices
$G=(V,E)$
is a set of vertices
![]() $V$
along with a set of edges
$V$
along with a set of edges
![]() $E$
each of which is a subset of
$E$
each of which is a subset of
![]() $V$
of size at least
$V$
of size at least
![]() $2$
. A hypergraph is
$2$
. A hypergraph is
![]() $k$
-uniform if all edges are of size
$k$
-uniform if all edges are of size
![]() $k$
. A
$k$
. A
![]() $2$
-uniform hypergraph is a graph. The degree of a vertex
$2$
-uniform hypergraph is a graph. The degree of a vertex
![]() $v \in V$
is the number of edges it appears in; in a hypergraph of maximum degree
$v \in V$
is the number of edges it appears in; in a hypergraph of maximum degree
![]() $\Delta$
, each vertex appears in at most
$\Delta$
, each vertex appears in at most
![]() $\Delta$
edges. An independent set in
$\Delta$
edges. An independent set in
![]() $G$
is a subset
$G$
is a subset
![]() $I \subseteq V$
that contains no edge
$I \subseteq V$
that contains no edge
![]() $e \in E$
. Let
$e \in E$
. Let
![]() $\mathcal I(G)$
denote the set of all independent sets of
$\mathcal I(G)$
denote the set of all independent sets of
![]() $G$
. The independence polynomial of the hypergraph
$G$
. The independence polynomial of the hypergraph
![]() $G$
is
$G$
is
Independence polynomials for graphs arise in numerous contexts in mathematics, physics, and computer science, including in the study of the Lovász Local Lemma in probabilistic combinatorics [Reference Scott and Sokal57, Reference Shearer58], in the study of the hard-core lattice gas in statistical physics [Reference Baxter5, Reference Galvin and Kahn27, Reference van den Berg and Maes61], and in algorithmic problems of approximate counting and sampling [Reference Sly59, Reference Weitz62].
In all of these settings, knowledge of the complex zeroes of
![]() $Z_G(\lambda )$
, or more precisely, knowledge of regions of
$Z_G(\lambda )$
, or more precisely, knowledge of regions of
![]() $\mathbb C$
uniformly free from zeroes of
$\mathbb C$
uniformly free from zeroes of
![]() $Z_G$
for some class of graphs, is crucial in understanding the phenomena of interest. For instance, as Shearer shows [Reference Shearer58] (and Scott and Sokal expand upon [Reference Scott and Sokal57]), the largest negative zero of
$Z_G$
for some class of graphs, is crucial in understanding the phenomena of interest. For instance, as Shearer shows [Reference Shearer58] (and Scott and Sokal expand upon [Reference Scott and Sokal57]), the largest negative zero of
![]() $Z_G(\lambda )$
provides the optimal bound for the Lovász Local Lemma for a set of events with a given dependency graph
$Z_G(\lambda )$
provides the optimal bound for the Lovász Local Lemma for a set of events with a given dependency graph
![]() $G$
; the Yang–Lee theory of phase transitions states that phase transitions can only occur where complex zeroes condense on the real axis [Reference Yang and Lee64]; and regions free of complex zeros for bounded-degree graphs may determine the computational complexity of the associated approximate counting problem [Reference Bezáková, Galanis, Goldberg and Stefankovic13, Reference Harvey, Srivastava and Vondrák32, Reference Peters and Regts49].
$G$
; the Yang–Lee theory of phase transitions states that phase transitions can only occur where complex zeroes condense on the real axis [Reference Yang and Lee64]; and regions free of complex zeros for bounded-degree graphs may determine the computational complexity of the associated approximate counting problem [Reference Bezáková, Galanis, Goldberg and Stefankovic13, Reference Harvey, Srivastava and Vondrák32, Reference Peters and Regts49].
For the class of graphs of maximum degree
![]() $\Delta$
, much is known about optimal zero-free regions. The optimal zero-free disc around
$\Delta$
, much is known about optimal zero-free regions. The optimal zero-free disc around
![]() $0$
has radius
$0$
has radius
that is, for any such
![]() $G$
and any
$G$
and any
![]() $\lambda \in \mathbb C$
with
$\lambda \in \mathbb C$
with
![]() $|\lambda | \lt \lambda _s(\Delta )$
,
$|\lambda | \lt \lambda _s(\Delta )$
,
![]() $Z_G(\lambda ) \ne 0$
[Reference Shearer58]. Moreover, this result is tight: for any
$Z_G(\lambda ) \ne 0$
[Reference Shearer58]. Moreover, this result is tight: for any
![]() $\epsilon \gt 0$
there is a graph of maximum degree
$\epsilon \gt 0$
there is a graph of maximum degree
![]() $\Delta$
with a zero of
$\Delta$
with a zero of
![]() $Z_G(\lambda )$
of magnitude at most
$Z_G(\lambda )$
of magnitude at most
![]() $\lambda _s(\Delta )+ \epsilon$
. In fact, this graph can be taken to be a tree, and even more specifically, a finite-depth truncation of the infinite
$\lambda _s(\Delta )+ \epsilon$
. In fact, this graph can be taken to be a tree, and even more specifically, a finite-depth truncation of the infinite
![]() $\Delta$
-regular tree. There are also known zero-free regions that are not discs; for instance, those that extend beyond the optimal zero-free disc in the direction of the positive real axis [Reference Bencs and Csikvári8, Reference Bencs, Csikvári, Srivastava and Vondrák10, Reference Buys17, Reference Peters and Regts49].
$\Delta$
-regular tree. There are also known zero-free regions that are not discs; for instance, those that extend beyond the optimal zero-free disc in the direction of the positive real axis [Reference Bencs and Csikvári8, Reference Bencs, Csikvári, Srivastava and Vondrák10, Reference Buys17, Reference Peters and Regts49].
In this paper we turn to the case of bounded-degree hypergraphs with hyperedges of size greater than
![]() $2$
. Our motivation is threefold.
$2$
. Our motivation is threefold.
-
(i) Statistical physics. In the language of statistical physics, the hard-core model on a graph is a model with pair interactions, while the hard-core model on a hypergraph with edges of size
 $\gt 2$
has multi-body interactions. Multi-body interactions are relevant for a range of physical phenomena, but they are also often more difficult to analyse on both a rigorous and non-rigorous level. There is a vast body of literature on the convergence properties of the cluster expansion in models with pair interactions [Reference Fernández and Procacci24, Reference Fernández, Procacci and Scoppola25, Reference Groeneveld29, Reference Nguyen and Fernández46, Reference Penrose48, Reference Procacci and Yuhjtman51, Reference Ruelle56], including bounds, like Shearer’s, that are optimal or near-optimal. The understanding of the convergence of the cluster expansion in models with multi-body interactions is much more limited, and bounds are typically non-effective (with respect to, say, graph degree), exclude interactions with a multi-body hard-core, or require a pairwise hard-core interaction in addition to a multi-body interaction [Reference Cassandro and Olivieri20, Reference Greenberg28, Reference Moraal44, Reference Procacci and Scoppola50, Reference Rebenko and Shchepan’uk53, Reference Rebenko54]. See the discussion in [Reference Brydges16, Reference Jansen and Tsagkarogiannis36] on obstacles to proving convergence of the multi-body cluster expansion.
$\gt 2$
has multi-body interactions. Multi-body interactions are relevant for a range of physical phenomena, but they are also often more difficult to analyse on both a rigorous and non-rigorous level. There is a vast body of literature on the convergence properties of the cluster expansion in models with pair interactions [Reference Fernández and Procacci24, Reference Fernández, Procacci and Scoppola25, Reference Groeneveld29, Reference Nguyen and Fernández46, Reference Penrose48, Reference Procacci and Yuhjtman51, Reference Ruelle56], including bounds, like Shearer’s, that are optimal or near-optimal. The understanding of the convergence of the cluster expansion in models with multi-body interactions is much more limited, and bounds are typically non-effective (with respect to, say, graph degree), exclude interactions with a multi-body hard-core, or require a pairwise hard-core interaction in addition to a multi-body interaction [Reference Cassandro and Olivieri20, Reference Greenberg28, Reference Moraal44, Reference Procacci and Scoppola50, Reference Rebenko and Shchepan’uk53, Reference Rebenko54]. See the discussion in [Reference Brydges16, Reference Jansen and Tsagkarogiannis36] on obstacles to proving convergence of the multi-body cluster expansion. -
(ii) Algorithms. Zero-free regions of independence polynomials (and graph polynomials and partition functions more generally) are closely linked to the computational complexity of approximate counting and sampling. Barvinok [Reference Barvinok2] developed an approach to approximate counting and sampling based on truncating the Taylor series (or cluster expansion) for
 $\log Z$
; the accuracy of this truncation relies on the existence of a zero-free region for
$\log Z$
; the accuracy of this truncation relies on the existence of a zero-free region for
 $Z$
. Refinements and applications of this method appear in, e.g., [Reference Barvinok3, Reference Barvinok and Soberón4, Reference Bencs, Davies, Patel and Regts11, Reference Harrow, Mehraban and Soleimanifar31, Reference Helmuth, Perkins and Regts33, Reference Liu, Sinclair and Srivastava42, Reference Patel and Regts47, Reference Regts55]. On the other hand, computational complexity results for approximate counting can be proved using the existence of complex zeroes of
$Z$
. Refinements and applications of this method appear in, e.g., [Reference Barvinok3, Reference Barvinok and Soberón4, Reference Bencs, Davies, Patel and Regts11, Reference Harrow, Mehraban and Soleimanifar31, Reference Helmuth, Perkins and Regts33, Reference Liu, Sinclair and Srivastava42, Reference Patel and Regts47, Reference Regts55]. On the other hand, computational complexity results for approximate counting can be proved using the existence of complex zeroes of
 $Z$
[Reference Bezáková, Galanis, Goldberg and Stefankovic13, Reference Bezáková, Galanis, Goldberg and Štefankovič14, Reference Buys, Galanis, Patel and Regts18, Reference de Boer, Buys, Guerini, Peters and Regts22, Reference Galanis, Goldberg and Herrera-Poyatos26].
$Z$
[Reference Bezáková, Galanis, Goldberg and Stefankovic13, Reference Bezáková, Galanis, Goldberg and Štefankovič14, Reference Buys, Galanis, Patel and Regts18, Reference de Boer, Buys, Guerini, Peters and Regts22, Reference Galanis, Goldberg and Herrera-Poyatos26]. -
(iii) Combinatorics. Beyond its application to the Lovász Local Lemma, the cluster expansion has been used recently as a tool in asymptotic enumeration, e.g., [Reference Balogh, Garcia and Li1, Reference Davies, Jenssen and Perkins21, Reference Jenssen and Keevash38–Reference Jenssen, Perkins and Potukuchi40]. The high-level idea in many of these applications is to interpret defects from an extremal configuration (or a simple set of configurations) in a combinatorial problem as a statistical physics model with a pair interaction and then use the cluster expansion to estimate the partition function of this new model. This approach is effective when typical configurations are very ‘ordered’, with structure that resembles a well understood extremal example with sparse defects. On the other hand, a powerful approach to asymptotic enumeration in the opposite regime, when typical configurations are unstructured, is that of Janson’s inequality and its extensions [Reference Janson, Luczak and Rucinski37, Reference Mousset, Noever, Panagiotou and Samotij45, Reference Stark and Wormald60, Reference Wormald63]. In its most commonly applied form, this approach estimates the partition function of a hypergraph hard-core model: the scaled probability that a
 $p$
-random subset of a ground set does not contain any of a specified family of subsets (the ground set is the vertex set and the family of subsets are the hyperedges of a hypergraph). The estimate for this general problem in [Reference Mousset, Noever, Panagiotou and Samotij45] takes the form of an exponential of a sum of terms defined in much the same way the terms of the cluster expansion are defined. That result, however, does not show convergence of the infinite series defined by the cluster expansion. If one could prove convergence, one could extend the results of [Reference Mousset, Noever, Panagiotou and Samotij45, Reference Stark and Wormald60] and deduce additional consequences through control of certain moment generating functions (as in, e.g., [Reference Cannon and Perkins19, Reference Jenssen and Perkins39] in the case of the graph cluster expansion). This application is perhaps our primary motivation for understanding zeroes of hypergraph independence polynomials, and it is the results of [Reference Mousset, Noever, Panagiotou and Samotij45] that suggest Conjecture 3.
$p$
-random subset of a ground set does not contain any of a specified family of subsets (the ground set is the vertex set and the family of subsets are the hyperedges of a hypergraph). The estimate for this general problem in [Reference Mousset, Noever, Panagiotou and Samotij45] takes the form of an exponential of a sum of terms defined in much the same way the terms of the cluster expansion are defined. That result, however, does not show convergence of the infinite series defined by the cluster expansion. If one could prove convergence, one could extend the results of [Reference Mousset, Noever, Panagiotou and Samotij45, Reference Stark and Wormald60] and deduce additional consequences through control of certain moment generating functions (as in, e.g., [Reference Cannon and Perkins19, Reference Jenssen and Perkins39] in the case of the graph cluster expansion). This application is perhaps our primary motivation for understanding zeroes of hypergraph independence polynomials, and it is the results of [Reference Mousset, Noever, Panagiotou and Samotij45] that suggest Conjecture 3.
1.1. Zero-freeness for hypergraph independence polynomials
Our first main result is that all hypergraphs satisfy a bound close to the Shearer bound for graphs.
Theorem 1.
Let
![]() $G$
be a hypergraph of maximum degree
$G$
be a hypergraph of maximum degree
![]() $\Delta$
. Suppose
$\Delta$
. Suppose
Then
![]() $Z_G(\lambda ) \ne 0$
.
$Z_G(\lambda ) \ne 0$
.
In Theorem 10 in Section 2 we will prove a stronger statement: in the multivariate setting in which each vertex
![]() $v$
receives its own activity
$v$
receives its own activity
![]() $\lambda _v$
,
$\lambda _v$
,
![]() $Z_G \ne 0$
when
$Z_G \ne 0$
when
![]() $|\lambda _v| \lt \lambda _s(\Delta +1)$
for all
$|\lambda _v| \lt \lambda _s(\Delta +1)$
for all
![]() $v$
.
$v$
.
The best previous bound on zero-free discs for hypergraph independence polynomials is due to Bencs, Csikvári, and Regts [Reference Bencs, Csikvári and Regts9, Corollary 6] who proved zero-freeness for
![]() $|\lambda |\leq 2^{-\Delta }$
.
$|\lambda |\leq 2^{-\Delta }$
.
The bound in Theorem 1 is nearly tight apart from the possible improvement of substituting
![]() $\Delta$
for
$\Delta$
for
![]() $\Delta +1$
in the bound (see Remark 11 below on one obstacle to this improvement). The examples that show this near tightness are graphs (the family of trees that prove tightness of Shearer’s result), and so one might hope that in a
$\Delta +1$
in the bound (see Remark 11 below on one obstacle to this improvement). The examples that show this near tightness are graphs (the family of trees that prove tightness of Shearer’s result), and so one might hope that in a
![]() $k$
-uniform hypergraph with
$k$
-uniform hypergraph with
![]() $k\gt 2$
an improvement is possible. Thanks to an example (provided to us by Wojciech Samotij), we know that in general no polynomial improvement in
$k\gt 2$
an improvement is possible. Thanks to an example (provided to us by Wojciech Samotij), we know that in general no polynomial improvement in
![]() $\Delta$
is possible.
$\Delta$
is possible.
Proposition 2.
For each
![]() $k \ge 3$
, there is a family of
$k \ge 3$
, there is a family of
![]() $k$
-uniform hypergraphs of maximum degree
$k$
-uniform hypergraphs of maximum degree
![]() $\Delta$
with smallest root
$\Delta$
with smallest root
![]() $\lambda$
satisfying
$\lambda$
satisfying
In Sections 4.1 and 4.2, we give the details of this construction.
Still one might hope that with additional conditions on the hypergraph a significant improvement might be obtained.
A hypergraph is linear if each pair of edges intersect in at most one vertex (a graph by definition must be linear). We conjecture that
![]() $k$
-uniform, linear hypergraphs of bounded degree have much larger zero-free discs.
$k$
-uniform, linear hypergraphs of bounded degree have much larger zero-free discs.
Conjecture 3.
For each
![]() $k \ge 2$
, there exists a constant
$k \ge 2$
, there exists a constant
![]() $C_k \gt 0$
, so that the following is true. If
$C_k \gt 0$
, so that the following is true. If
![]() $G$
is a
$G$
is a
![]() $k$
-uniform, linear hypergraph of maximum degree
$k$
-uniform, linear hypergraph of maximum degree
![]() $\Delta$
and if
$\Delta$
and if
then
![]() $Z_G(\lambda ) \ne 0$
.
$Z_G(\lambda ) \ne 0$
.
The case
![]() $k=2$
is proved by Shearer’s theorem; for larger
$k=2$
is proved by Shearer’s theorem; for larger
![]() $k$
the conjecture posits a polynomial improvement to the bound of Theorem 1.
$k$
the conjecture posits a polynomial improvement to the bound of Theorem 1.
We can prove Conjecture 3 in a special case. A linear hypertree is a connected, linear hypergraph with a unique path between any pair of vertices. We next show that linear hypertrees satisfy the bound of Conjecture 3.
Theorem 4.
For each
![]() $k \ge 2$
the following is true. If
$k \ge 2$
the following is true. If
![]() $G$
is a
$G$
is a
![]() $k$
-uniform, linear hypertree of maximum degree
$k$
-uniform, linear hypertree of maximum degree
![]() $\Delta$
and if
$\Delta$
and if
then
![]() $Z_G(\lambda ) \ne 0$
. In particular,
$Z_G(\lambda ) \ne 0$
. In particular,
implies
![]() $Z_G(\lambda ) \ne 0$
.
$Z_G(\lambda ) \ne 0$
.
The following example shows that one cannot hope for a polynomial improvement in
![]() $\Delta$
to this bound (or to the bound conjectured in Conjecture 3).
$\Delta$
to this bound (or to the bound conjectured in Conjecture 3).
Proposition 5.
For each even
![]() $k \ge 4$
there is a family of
$k \ge 4$
there is a family of
![]() $k$
-uniform hypergraphs of maximum degree
$k$
-uniform hypergraphs of maximum degree
![]() $\Delta$
with smallest root
$\Delta$
with smallest root
![]() $\lambda$
satisfying
$\lambda$
satisfying
 \begin{equation*} |\lambda | = O \left ( \left (\frac {\log \Delta }{\Delta }\right )^{\frac {1}{k-1}} \right ) \,.\end{equation*}
\begin{equation*} |\lambda | = O \left ( \left (\frac {\log \Delta }{\Delta }\right )^{\frac {1}{k-1}} \right ) \,.\end{equation*}
This lower bound is achieved by the
![]() $k$
-uniform star with
$k$
-uniform star with
![]() $\Delta$
edges. The details are in Section 4.3.
$\Delta$
edges. The details are in Section 4.3.
Finally we make a conjecture about the zero-free locus of independence polynomials of bounded-degree hypergraphs. Using the notation from, e.g., [Reference Bencs, Buys and Peters7, Reference Buys17, Reference de Boer, Buys, Guerini, Peters and Regts22], let
![]() $\mathcal U_{\Delta }$
denote the maximal simply connected open set in
$\mathcal U_{\Delta }$
denote the maximal simply connected open set in
![]() $\mathbb C$
containing
$\mathbb C$
containing
![]() $0$
that is zero-free for independence polynomials of all graphs of maximum degree
$0$
that is zero-free for independence polynomials of all graphs of maximum degree
![]() $\Delta$
. Extending this notation, let
$\Delta$
. Extending this notation, let
![]() $\mathcal U_{\Delta,k}$
be the same for
$\mathcal U_{\Delta,k}$
be the same for
![]() $k$
-uniform hypergraphs (so
$k$
-uniform hypergraphs (so
![]() $\mathcal U_{\Delta } = \mathcal U_{\Delta,2}$
); and
$\mathcal U_{\Delta } = \mathcal U_{\Delta,2}$
); and
![]() $\mathcal U_{\Delta, \ge k}$
the same for hypergraphs with edge size at least
$\mathcal U_{\Delta, \ge k}$
the same for hypergraphs with edge size at least
![]() $k$
. In particular, Theorem 1 shows that
$k$
. In particular, Theorem 1 shows that
![]() $\mathcal U_{\Delta,\ge 2}$
contains a disc of radius
$\mathcal U_{\Delta,\ge 2}$
contains a disc of radius
![]() $\lambda _s(\Delta +1)$
.
$\lambda _s(\Delta +1)$
.
Conjecture 6.
The zero-free locus of hypergraphs of maximum degree
![]() $\Delta$
is identical to the zero-free locus of graphs of maximum degree
$\Delta$
is identical to the zero-free locus of graphs of maximum degree
![]() $\Delta$
; that is,
$\Delta$
; that is,
![]() $\mathcal U_{\Delta, \ge 2} = \mathcal U_{\Delta }$
.
$\mathcal U_{\Delta, \ge 2} = \mathcal U_{\Delta }$
.
Conjecture 6 in particular implies that one can replace
![]() $\lambda _s(\Delta +1)$
by
$\lambda _s(\Delta +1)$
by
![]() $\lambda _s(\Delta )$
in Theorem 1. The next question asks if in fact increasing
$\lambda _s(\Delta )$
in Theorem 1. The next question asks if in fact increasing
![]() $k$
strictly enlarges the zero-free locus.
$k$
strictly enlarges the zero-free locus.
Question 7.
Is it true that for any
![]() $\Delta \ge 2$
,
$\Delta \ge 2$
,
![]() $k\ge 2$
, we have the strict containment
$k\ge 2$
, we have the strict containment
Remark 8. Since the appearance of a preprint of this paper, Zhang [Reference Zhang65] has disproved Conjecture 3, constructing, for each
![]() $k \ge 3$
, a family of
$k \ge 3$
, a family of
![]() $k$
-uniform, linear hypergraphs of maximum degree
$k$
-uniform, linear hypergraphs of maximum degree
![]() $\Delta$
with smallest root
$\Delta$
with smallest root
![]() $O \left ( \frac{\log \Delta }{\Delta } \right )$
. Reconciling this counterexample with the results of [Reference Mousset, Noever, Panagiotou and Samotij45] is an interesting direction for future research. Moreover, Bencs and Buys [Reference Bencs and Buys6] have disproved Conjecture 6, though they have confirmed it in an asymptotic sense as
$O \left ( \frac{\log \Delta }{\Delta } \right )$
. Reconciling this counterexample with the results of [Reference Mousset, Noever, Panagiotou and Samotij45] is an interesting direction for future research. Moreover, Bencs and Buys [Reference Bencs and Buys6] have disproved Conjecture 6, though they have confirmed it in an asymptotic sense as
![]() $\Delta \to \infty$
and proved that one can replace the bound of
$\Delta \to \infty$
and proved that one can replace the bound of
![]() $\lambda _s(\Delta +1)$
in Theorem 1 with
$\lambda _s(\Delta +1)$
in Theorem 1 with
![]() $\lambda _s(\Delta )$
, which is optimal.
$\lambda _s(\Delta )$
, which is optimal.
1.2 Algorithms
To describe the algorithmic consequences of Theorem 1, we recall some basics of approximate counting and sampling. A complex number
![]() $\hat Z$
is an
$\hat Z$
is an
![]() $\epsilon$
-relative approximation to a complex number
$\epsilon$
-relative approximation to a complex number
![]() $Z$
if
$Z$
if
An FPTAS (fully polynomial time approximation scheme) for a complex-valued graph polynomial
![]() $Z_G$
is an algorithm that, given
$Z_G$
is an algorithm that, given
![]() $G$
and
$G$
and
![]() $\epsilon$
, outputs an
$\epsilon$
, outputs an
![]() $\epsilon$
-relative approximation to
$\epsilon$
-relative approximation to
![]() $Z_G$
and runs in time polynomial in
$Z_G$
and runs in time polynomial in
![]() $|V(G)|$
and
$|V(G)|$
and
![]() $1/\epsilon$
.
$1/\epsilon$
.
Theorem 9.
For the class of hypergraphs
![]() $G$
of maximum degree
$G$
of maximum degree
![]() $\Delta$
and maximum edge size
$\Delta$
and maximum edge size
![]() $k$
, there is an FPTAS for
$k$
, there is an FPTAS for
![]() $Z_G(\lambda )$
when
$Z_G(\lambda )$
when
![]() $| \lambda | \lt \lambda _s(\Delta +1)$
.
$| \lambda | \lt \lambda _s(\Delta +1)$
.
The algorithm proceeds by truncating the cluster expansion (the Taylor series for
![]() $\log Z_G(\lambda )$
around
$\log Z_G(\lambda )$
around
![]() $0$
); that is, using Barvinok’s polynomial interpolation method. The fact that the exponential of the truncation provides a good approximation to
$0$
); that is, using Barvinok’s polynomial interpolation method. The fact that the exponential of the truncation provides a good approximation to
![]() $Z_G$
follows from the zero-freeness result of Theorem 1 and Barvinok’s approximation lemma [Reference Barvinok2, Lemma 2.2.1]. The only additional ingredient is to show that the coefficients of the cluster expansion can be computed efficiently: we need to compute the coefficient of
$Z_G$
follows from the zero-freeness result of Theorem 1 and Barvinok’s approximation lemma [Reference Barvinok2, Lemma 2.2.1]. The only additional ingredient is to show that the coefficients of the cluster expansion can be computed efficiently: we need to compute the coefficient of
![]() $\lambda ^r$
in time
$\lambda ^r$
in time
![]() $\exp (O (r))$
where the implied constant in the
$\exp (O (r))$
where the implied constant in the
![]() $O(\cdot )$
may depend on
$O(\cdot )$
may depend on
![]() $\Delta,k,$
and
$\Delta,k,$
and
![]() $\lambda$
, since we treat these as constants. For graphs, Patel and Regts [Reference Patel and Regts47] showed how to compute these coefficients efficiently; the extension to hypergraphs was done by Liu, Sinclair, Srivastava [Reference Liu, Sinclair and Srivastava42]. We give the details of the algorithm in Section 5. Note that there is no dependence on
$\lambda$
, since we treat these as constants. For graphs, Patel and Regts [Reference Patel and Regts47] showed how to compute these coefficients efficiently; the extension to hypergraphs was done by Liu, Sinclair, Srivastava [Reference Liu, Sinclair and Srivastava42]. We give the details of the algorithm in Section 5. Note that there is no dependence on
![]() $k$
in the bound on
$k$
in the bound on
![]() $\lambda$
; the running time of the algorithm, however, grows like
$\lambda$
; the running time of the algorithm, however, grows like
![]() $n^{O(\log k +\log \Delta )}$
and so is only polynomial-time when
$n^{O(\log k +\log \Delta )}$
and so is only polynomial-time when
![]() $k$
and
$k$
and
![]() $\Delta$
are constants.
$\Delta$
are constants.
Previous algorithmic work on hypergraph independent sets has primarily focused on the case
![]() $\lambda =1$
; that is, approximately counting the number of independent sets in a hypergraph (and sampling approximately uniformly). The algorithmic results here generally fall into two categories: randomised approximation algorithms (yielding an FPRAS) based on Markov chain Monte Carlo and deterministic approximation algorithms (yielding an FPTAS) based on the method of correlation decay pioneered by Weitz [Reference Weitz62]. Examples of the first type of result include [Reference Bordewich, Dyer and Karpinski15, Reference Hermon, Sly and Zhang34, Reference Qiu, Wang and Zhang52]; while the second set of results include [Reference Bezáková, Galanis, Goldberg, Guo and Stefankovic12, Reference Liu and Lu41]. In [Reference Liu and Lu41], Liu and Lu show that there is an FPTAS for counting independent sets in hypergraphs of maximum degree
$\lambda =1$
; that is, approximately counting the number of independent sets in a hypergraph (and sampling approximately uniformly). The algorithmic results here generally fall into two categories: randomised approximation algorithms (yielding an FPRAS) based on Markov chain Monte Carlo and deterministic approximation algorithms (yielding an FPTAS) based on the method of correlation decay pioneered by Weitz [Reference Weitz62]. Examples of the first type of result include [Reference Bordewich, Dyer and Karpinski15, Reference Hermon, Sly and Zhang34, Reference Qiu, Wang and Zhang52]; while the second set of results include [Reference Bezáková, Galanis, Goldberg, Guo and Stefankovic12, Reference Liu and Lu41]. In [Reference Liu and Lu41], Liu and Lu show that there is an FPTAS for counting independent sets in hypergraphs of maximum degree
![]() $5$
, matching the bound for independent sets in graphs due to Weitz [Reference Weitz62] (like Theorem 1, this says things are no worse for hypergraphs that they are for graphs). In [Reference Bezáková, Galanis, Goldberg, Guo and Stefankovic12], Bezáková, Galanis, Goldberg, and Štefankovič study the case when
$5$
, matching the bound for independent sets in graphs due to Weitz [Reference Weitz62] (like Theorem 1, this says things are no worse for hypergraphs that they are for graphs). In [Reference Bezáková, Galanis, Goldberg, Guo and Stefankovic12], Bezáková, Galanis, Goldberg, and Štefankovič study the case when
![]() $\lambda =1$
and
$\lambda =1$
and
![]() $k \ge 3$
; in this case they can surpass the graph bound; e.g., giving an FPTAS for
$k \ge 3$
; in this case they can surpass the graph bound; e.g., giving an FPTAS for
![]() $k$
-uniform hypergraphs when
$k$
-uniform hypergraphs when
![]() $\Delta \le 6$
(as opposed to
$\Delta \le 6$
(as opposed to
![]() $\Delta \le 5$
for graphs). Moreover they give an FPTAS when
$\Delta \le 5$
for graphs). Moreover they give an FPTAS when
![]() $\Delta \le k$
, a large improvement over the graph bound when
$\Delta \le k$
, a large improvement over the graph bound when
![]() $k$
is large. Finally, there has been significant recent interest in a generalisation of this counting problem, that of approximately counting the number of solutions to
$k$
is large. Finally, there has been significant recent interest in a generalisation of this counting problem, that of approximately counting the number of solutions to
![]() $k$
-CNF formulas. The case of independent sets in
$k$
-CNF formulas. The case of independent sets in
![]() $k$
-uniform hypergraphs is the special case of counting solutions to monotone
$k$
-uniform hypergraphs is the special case of counting solutions to monotone
![]() $k$
-CNF formulas. Work on this problem includes [Reference Feng, Guo, Yin and Zhang23, Reference Guo, Jerrum and Liu30, Reference Jain, Pham and Vuong35, Reference Moitra43]. It is an interesting direction to explore the connections between these results and the results and questions in the current paper.
$k$
-CNF formulas. Work on this problem includes [Reference Feng, Guo, Yin and Zhang23, Reference Guo, Jerrum and Liu30, Reference Jain, Pham and Vuong35, Reference Moitra43]. It is an interesting direction to explore the connections between these results and the results and questions in the current paper.
2. Zero-free regions for bounded-degree hypergraphs
We begin by generalising the independence polynomial to the multivariate case. Let
![]() ${\boldsymbol{\lambda }}= (\lambda _v\,{:}\,v \in V)$
be a collection of (possibly complex) activities on the vertices of
${\boldsymbol{\lambda }}= (\lambda _v\,{:}\,v \in V)$
be a collection of (possibly complex) activities on the vertices of
![]() $G$
. The multivariate independence polynomial of
$G$
. The multivariate independence polynomial of
![]() $G$
at
$G$
at
![]() $e$
is
$e$
is
where
![]() ${\mathcal I}(G)$
is the set of all independent sets of
${\mathcal I}(G)$
is the set of all independent sets of
![]() $G$
. If all
$G$
. If all
![]() $\lambda _v$
have the same value,
$\lambda _v$
have the same value,
![]() $\lambda$
say, then
$\lambda$
say, then
![]() $Z_{G}(\boldsymbol{\lambda })$
is the independence polynomial defined in Section 1.
$Z_{G}(\boldsymbol{\lambda })$
is the independence polynomial defined in Section 1.
The main goal of this section is to prove the following zero-freeness result for the mulitivariate independence polynomial of bounded-degree hypergraph.
Theorem 10.
Let
![]() $G$
be a hypergraph of maximum degree
$G$
be a hypergraph of maximum degree
![]() $\Delta$
. If
$\Delta$
. If
![]() $|\lambda _v|\leq \frac{\Delta ^\Delta }{(\Delta +1)^{\Delta +1}}$
for all
$|\lambda _v|\leq \frac{\Delta ^\Delta }{(\Delta +1)^{\Delta +1}}$
for all
![]() $v\in V$
, then
$v\in V$
, then
Note that
![]() $\Delta ^\Delta/(\Delta +1)^{(\Delta +1)} \sim 1/e\Delta$
as
$\Delta ^\Delta/(\Delta +1)^{(\Delta +1)} \sim 1/e\Delta$
as
![]() $\Delta \rightarrow \infty$
. As discussed above, this theorem is tight apart from the possible substitution of
$\Delta \rightarrow \infty$
. As discussed above, this theorem is tight apart from the possible substitution of
![]() $\Delta$
for
$\Delta$
for
![]() $\Delta +1$
in the bound.
$\Delta +1$
in the bound.
The proof of Theorem 10 follows the broad outline of the proof of Shearer’s theorem in [Reference Scott and Sokal57, Reference Shearer58]. While the proof for graphs involves the operation of removing vertices from a graph, the extension to hypergraphs is more involved: the operations we perform include removing vertices from a hypergraph as well as shrinking edges. To keep track of these operations and to be explicit about edge and vertex sets, we will use the notation
![]() $Z_{V,E}(\boldsymbol{\lambda })$
for
$Z_{V,E}(\boldsymbol{\lambda })$
for
![]() $Z_G(\boldsymbol{\lambda })$
where
$Z_G(\boldsymbol{\lambda })$
where
![]() $G= (V,E)$
.
$G= (V,E)$
.
For
![]() $A\subset V$
with
$A\subset V$
with
![]() $A \neq \emptyset$
, we define the following operations on the edge set
$A \neq \emptyset$
, we define the following operations on the edge set
![]() $E$
, whose utility will become apparent when we present (2.1) and (2.2), the basic deletion/contraction identities for
$E$
, whose utility will become apparent when we present (2.1) and (2.2), the basic deletion/contraction identities for
![]() $Z_{V,E}(\boldsymbol{\lambda })$
:
$Z_{V,E}(\boldsymbol{\lambda })$
:
-
Deletion
 $E-A$
is the set of edges that avoid
$E-A$
is the set of edges that avoid
 $A$
, that is,For
$A$
, that is,For \begin{equation*} E-A =\{e \in E\,{:}\,e \cap A =\emptyset \}. \end{equation*}
\begin{equation*} E-A =\{e \in E\,{:}\,e \cap A =\emptyset \}. \end{equation*}
 $v \in V$
we write
$v \in V$
we write
 $E-v$
for
$E-v$
for
 $E-\{v\}$
.
$E-\{v\}$
.
-
Contraction
 $E/A$
is the set of edges of size at least
$E/A$
is the set of edges of size at least
 $2$
that are created by deleting the elements of
$2$
that are created by deleting the elements of
 $A$
from all the edges in
$A$
from all the edges in
 $E$
, that is,For
$E$
, that is,For \begin{equation*} E/A=(E-A)\cup \{e\setminus A\,{:}\,e\cap A\neq \emptyset,|e\setminus A|\geq 2\}. \end{equation*}
\begin{equation*} E/A=(E-A)\cup \{e\setminus A\,{:}\,e\cap A\neq \emptyset,|e\setminus A|\geq 2\}. \end{equation*}
 $v \in V$
we write
$v \in V$
we write
 $E/v$
for
$E/v$
for
 $E/\{v\}$
.
$E/\{v\}$
.
-
Closure
 $C(A)$
is the set of vertices outside
$C(A)$
is the set of vertices outside
 $A$
that, together with some non-empty subset of
$A$
that, together with some non-empty subset of
 $A$
, form an edge in
$A$
, form an edge in
 $E$
; in other words, each of which forms an edge with any (nonempty) subset of
$E$
; in other words, each of which forms an edge with any (nonempty) subset of
 $A$
. In other words, it is the set of edges of size
$A$
. In other words, it is the set of edges of size
 $1$
that are created by deleting the elements of
$1$
that are created by deleting the elements of
 $A$
from all the edges in
$A$
from all the edges in
 $E$
. Formally,For
$E$
. Formally,For \begin{equation*} C(A)=\{v\,{:}\,\text {there is } e\in E \text { with } e\setminus A=\{v\}\}. \end{equation*}
\begin{equation*} C(A)=\{v\,{:}\,\text {there is } e\in E \text { with } e\setminus A=\{v\}\}. \end{equation*}
 $v \in V$
we write
$v \in V$
we write
 $C(v)$
for
$C(v)$
for
 $C(\{v\})$
.
$C(\{v\})$
.
-
Edge addition
 $E+A$
is obtained from
$E+A$
is obtained from
 $E$
by including also
$E$
by including also
 $A$
as an edge, i.e.,
$A$
as an edge, i.e.,
 $E+A=E \cup \{A\}$
.
$E+A=E \cup \{A\}$
.
We will use two fundamental identities relating the independence polynomial of a hypergraph to that of some smaller hypergraphs. Note that here (and throughout) we abuse notation somewhat: if
![]() $\boldsymbol{\lambda }$
is a set of weights indexed by a set
$\boldsymbol{\lambda }$
is a set of weights indexed by a set
![]() $W$
, and
$W$
, and
![]() $W' \subseteq W$
, then we write
$W' \subseteq W$
, then we write
![]() $Z_{W',E'}(\boldsymbol{\lambda })$
when we actually mean
$Z_{W',E'}(\boldsymbol{\lambda })$
when we actually mean
![]() $Z_{W',E'}(\boldsymbol{\lambda }')$
, with
$Z_{W',E'}(\boldsymbol{\lambda }')$
, with
![]() $\boldsymbol{\lambda }'$
the restriction of the vector
$\boldsymbol{\lambda }'$
the restriction of the vector
![]() $\boldsymbol{\lambda }$
to the index set
$\boldsymbol{\lambda }$
to the index set
![]() $W'$
.
$W'$
.
Firstly we have that for any
![]() $v \in V$
,
$v \in V$
,
The identity follows by first considering those independent sets in
![]() $G$
that do not contain
$G$
that do not contain
![]() $v$
and then those that do.
$v$
and then those that do.
Secondly, for all
![]() $A \subseteq V$
such that there is no
$A \subseteq V$
such that there is no
![]() $e \in E$
with
$e \in E$
with
![]() $e \subseteq A$
we have
$e \subseteq A$
we have
This identity follow by observing that all independent sets in
![]() $(V,E)$
are independent sets in
$(V,E)$
are independent sets in
![]() $(V,E+A)$
, except those that contain all of
$(V,E+A)$
, except those that contain all of
![]() $A$
; and the extensions of
$A$
; and the extensions of
![]() $A$
to an independent set in
$A$
to an independent set in
![]() $(V,E)$
are precisely the independent sets in
$(V,E)$
are precisely the independent sets in
![]() $V\setminus (A \cup C(A)),E/A$
. Note that if there is an
$V\setminus (A \cup C(A)),E/A$
. Note that if there is an
![]() $e \in E$
with
$e \in E$
with
![]() $e \subseteq A$
then (2.2) becomes the simpler
$e \subseteq A$
then (2.2) becomes the simpler
For brevity, in what follows we will write
-
•
 $G-v$
for the hypergraph
$G-v$
for the hypergraph
 $(V\setminus \{v\},E-v)$
, and
$(V\setminus \{v\},E-v)$
, and
 $G-A$
for
$G-A$
for
 $(V\setminus A,E-A)$
$(V\setminus A,E-A)$
-
•
 $G/v$
for
$G/v$
for
 $(V \setminus (\{v\}\cup C(v),E/v)$
,
$(V \setminus (\{v\}\cup C(v),E/v)$
, -
•
 $G+A$
for
$G+A$
for
 $(V,E+A)$
and
$(V,E+A)$
and -
•
 $G/A$
for
$G/A$
for
 $(V\setminus (A \cup C(A)),E/A)$
.
$(V\setminus (A \cup C(A)),E/A)$
.
With this notation, (2.1) and (2.2) become
and
We define a collection of admissible subhypergraphs of
![]() $G=(V,E)$
as follows:
$G=(V,E)$
as follows:
![]() $G$
itself is admissible, and if
$G$
itself is admissible, and if
![]() $M=(V_M,E_M)$
is some admissible subhypergraph of
$M=(V_M,E_M)$
is some admissible subhypergraph of
![]() $G$
, then so are each of
$G$
, then so are each of
-
•
 $M-v$
and
$M-v$
and
 $M/v$
for any
$M/v$
for any
 $v \in V_M$
,
$v \in V_M$
, -
•
 $M+A$
and
$M+A$
and
 $M/A$
where
$M/A$
where
 $A\subseteq V_M$
is any proper subset of an
$A\subseteq V_M$
is any proper subset of an
 $e \in E_G\setminus E_M$
.
$e \in E_G\setminus E_M$
.
We are now ready to present the proof of Theorem 10.
Proof of Theorem 10. The overall plan is to show that as long as the hypothesised condition on
![]() $\boldsymbol{\lambda }$
holds, we have that if
$\boldsymbol{\lambda }$
holds, we have that if
![]() $M$
is any non-empty admissible subhypergraph of
$M$
is any non-empty admissible subhypergraph of
![]() $G$
and
$G$
and
![]() $v$
is any vertex in
$v$
is any vertex in
![]() $V_M$
then
$V_M$
then
where
![]() $s\lt 1$
may be chosen to be independent
$s\lt 1$
may be chosen to be independent
![]() $M$
and
$M$
and
![]() $v$
. Iterating this over an ordering
$v$
. Iterating this over an ordering
![]() $v_1, v_2, \ldots, v_{|V(G)|}$
of the vertices of
$v_1, v_2, \ldots, v_{|V(G)|}$
of the vertices of
![]() $G$
then yields, via a telescoping product,
$G$
then yields, via a telescoping product,
 \begin{equation} |Z_M(\boldsymbol{\lambda })| = \prod _{i=1}^{|V(G)|} \left |\frac{Z_{G-\{v_1, \ldots, v_{i-1}\}}(\boldsymbol{\lambda })}{Z_{G-\{v_1, \ldots, v_i\}}(\boldsymbol{\lambda })}\right | \geq (1-s)^{|V(G)|} \gt 0. \end{equation}
\begin{equation} |Z_M(\boldsymbol{\lambda })| = \prod _{i=1}^{|V(G)|} \left |\frac{Z_{G-\{v_1, \ldots, v_{i-1}\}}(\boldsymbol{\lambda })}{Z_{G-\{v_1, \ldots, v_i\}}(\boldsymbol{\lambda })}\right | \geq (1-s)^{|V(G)|} \gt 0. \end{equation}
To do this, we will need to control how the independence polynomial changes in going from
![]() $M$
to
$M$
to
![]() $M-v$
. It will turn out that in tandem with this we will also need to control how it changes in going from
$M-v$
. It will turn out that in tandem with this we will also need to control how it changes in going from
![]() $M$
to
$M$
to
![]() $M+A$
. To achieve both of these tasks, we will carry out a parallel induction.
$M+A$
. To achieve both of these tasks, we will carry out a parallel induction.
To state the induction hypothesis precisely, we introduce some notation. For an admissible subhypergraph
![]() $M=(V_M,E_M)$
, and a non-empty subset
$M=(V_M,E_M)$
, and a non-empty subset
![]() $A \subseteq V_M$
with
$A \subseteq V_M$
with
![]() $|A|=a$
, we define, for each positive integer
$|A|=a$
, we define, for each positive integer
![]() $b$
, the quantity
$b$
, the quantity
when
![]() $a=1$
or
$a=1$
or
![]() $a\gt 1$
and
$a\gt 1$
and
![]() $b\gt 1$
. Note that if
$b\gt 1$
. Note that if
![]() $A=\{v\}$
(so
$A=\{v\}$
(so
![]() $a=1$
) then
$a=1$
) then
![]() $n_{ab}$
is simply the number of edges in
$n_{ab}$
is simply the number of edges in
![]() $M$
of size
$M$
of size
![]() $b+1$
that include
$b+1$
that include
![]() $v$
.
$v$
.
For
![]() $b=1$
and
$b=1$
and
![]() $a\gt 1$
, we slightly modify this to
$a\gt 1$
, we slightly modify this to
i.e.,
![]() $n_{a1}=\#\left (2\text{-edges incident to }A\right )+|A|$
.
$n_{a1}=\#\left (2\text{-edges incident to }A\right )+|A|$
.
In the notation we suppress the dependence of
![]() $n_{ab}$
on
$n_{ab}$
on
![]() $M$
and
$M$
and
![]() $A$
.
$A$
.
We are now ready to state the main result of this section precisely. Let
![]() $R\gt 0$
and
$R\gt 0$
and
![]() $s_j \in (0,1)$
,
$s_j \in (0,1)$
,
![]() $j=1, 2, \ldots$
be constants that satisfy the following conditions for every admissible subhypergraph
$j=1, 2, \ldots$
be constants that satisfy the following conditions for every admissible subhypergraph
![]() $M=(V_M,E_M)$
of
$M=(V_M,E_M)$
of
![]() $G$
:
$G$
:
-
• For every
 $A \subseteq V_M$
with
$A \subseteq V_M$
with
 $|A|=1$
(i.e., every
$|A|=1$
(i.e., every
 $v \in V_M$
) we have(2.6)
$v \in V_M$
) we have(2.6) \begin{equation} R \leq s_1 \prod _{i \geq 1} (1-s_i)^{n_{1i}}, \end{equation}
\begin{equation} R \leq s_1 \prod _{i \geq 1} (1-s_i)^{n_{1i}}, \end{equation}
-
• and for every
 $A \subseteq M$
with
$A \subseteq M$
with
 $|A|=j\geq 2$
such that
$|A|=j\geq 2$
such that
 $M+A$
is admissible we have(2.7)
$M+A$
is admissible we have(2.7) \begin{equation} R^j \leq s_j \prod _{i \geq 1} (1-s_i)^{n_{ji}}. \end{equation}
\begin{equation} R^j \leq s_j \prod _{i \geq 1} (1-s_i)^{n_{ji}}. \end{equation}
Here, finally, is the statement that we will prove. Let
![]() $\boldsymbol{\lambda }$
be such that
$\boldsymbol{\lambda }$
be such that
![]() $|w_x| \leq R$
for all
$|w_x| \leq R$
for all
![]() $x \in V$
. Let
$x \in V$
. Let
![]() $M=(V_M,E_M)$
be an admissible subhypergraph of
$M=(V_M,E_M)$
be an admissible subhypergraph of
![]() $G$
. For
$G$
. For
![]() $v \in V_M$
we have
$v \in V_M$
we have
while for
![]() $A \subseteq M$
with
$A \subseteq M$
with
![]() $|A|=j\geq 2$
such that
$|A|=j\geq 2$
such that
![]() $M+A$
is admissible we have
$M+A$
is admissible we have
Before proving (2.8) and (2.9), we show that it is enough to complete the proof of Theorem 10. The key observations are that for any admissible
![]() $M$
and
$M$
and
![]() $v \in V_M$
we have
$v \in V_M$
we have
and for any admissible
![]() $M$
and
$M$
and
![]() $A \subseteq M$
with
$A \subseteq M$
with
![]() $|A|=a\geq 2$
such that
$|A|=a\geq 2$
such that
![]() $M+A$
is admissible we have
$M+A$
is admissible we have
Indeed, consider
![]() $x \in A$
. This is in at most
$x \in A$
. This is in at most
![]() $\Delta -1$
edges of
$\Delta -1$
edges of
![]() $M$
, since
$M$
, since
![]() $M+A$
is admissible which means
$M+A$
is admissible which means
![]() $x$
has degree at most
$x$
has degree at most
![]() $\Delta$
in
$\Delta$
in
![]() $M+A$
. Thus there are at most
$M+A$
. Thus there are at most
![]() $\Delta -1$
$\Delta -1$
![]() $S$
’s disjoint from
$S$
’s disjoint from
![]() $A$
such that
$A$
such that
![]() $S \cup T \in E_M$
with
$S \cup T \in E_M$
with
![]() $T \subseteq A$
and
$T \subseteq A$
and
![]() $x \in T$
. Since
$x \in T$
. Since
![]() $|A|=a$
, it follows that there are at most
$|A|=a$
, it follows that there are at most
![]() $a(\Delta -1)$
$a(\Delta -1)$
![]() $S$
’s disjoint from
$S$
’s disjoint from
![]() $A$
such that
$A$
such that
![]() $S \cup T \in E_M$
with
$S \cup T \in E_M$
with
![]() $T \subseteq A$
and
$T \subseteq A$
and
![]() $T \neq \emptyset$
. We now add the
$T \neq \emptyset$
. We now add the
![]() $a$
vertices of
$a$
vertices of
![]() $|A|$
deleted to get
$|A|$
deleted to get
![]() $a\Delta$
as a bound.
$a\Delta$
as a bound.
It follows that if we let all
![]() $s_i$
’s have a common value,
$s_i$
’s have a common value,
![]() $s$
say, then (2.6) and (2.7) are implied by:
$s$
say, then (2.6) and (2.7) are implied by:
for
![]() $j=1, 2, \ldots\,$
. Since
$j=1, 2, \ldots\,$
. Since
![]() $s \in (0,1)$
, all of these are implied by
$s \in (0,1)$
, all of these are implied by
![]() $R \leq s(1-s)^\Delta$
. We may now take
$R \leq s(1-s)^\Delta$
. We may now take
![]() $s=1/(\Delta +1)$
, leading to
$s=1/(\Delta +1)$
, leading to
![]() $R=\Delta ^\Delta/(\Delta +1)^{(\Delta +1)}$
. Theorem 10 now follows via the telescoping product (2.5).
$R=\Delta ^\Delta/(\Delta +1)^{(\Delta +1)}$
. Theorem 10 now follows via the telescoping product (2.5).
Now, to prove (2.8) and (2.9), we will proceed by induction on
![]() $|V_M|$
, showing firstly that an
$|V_M|$
, showing firstly that an
![]() $|M|=n+1$
instance of (2.8) can be deduced from (2.8) and (2.9) for
$|M|=n+1$
instance of (2.8) can be deduced from (2.8) and (2.9) for
![]() $|M|\leq n$
, and secondly that an
$|M|\leq n$
, and secondly that an
![]() $|M|=n+1$
instance of (2.9) can be deduced from (2.8) for
$|M|=n+1$
instance of (2.9) can be deduced from (2.8) for
![]() $|M|\leq n+1$
and (2.9) for
$|M|\leq n+1$
and (2.9) for
![]() $|M|\leq n$
.
$|M|\leq n$
.
As a base case we take
![]() $M=\varnothing$
, where both (2.8) and (2.9) are vacuously true.
$M=\varnothing$
, where both (2.8) and (2.9) are vacuously true.
For the first of the induction steps, assume that (2.8) and (2.9) both hold for all admissible
![]() $M'$
with
$M'$
with
![]() $|V_{M'}|\leq n$
, and let
$|V_{M'}|\leq n$
, and let
![]() $M=(V_M,E_M)$
be an admissible subhypergraph of
$M=(V_M,E_M)$
be an admissible subhypergraph of
![]() $G$
with
$G$
with
![]() $|V_M|=n+1$
vertices. Let
$|V_M|=n+1$
vertices. Let
![]() $v$
be any vertex of
$v$
be any vertex of
![]() $M$
. To show that (2.8) holds, we begin by applying identity (2.3):
$M$
. To show that (2.8) holds, we begin by applying identity (2.3):
Via the reverse triangle inequality and the assumption
![]() $|\lambda _v|\leq R$
, this gives
$|\lambda _v|\leq R$
, this gives
To extract our desired lower bound on
![]() $|Z_M(\boldsymbol{\lambda })|$
we will use the induction hypotheses (for admissible subhypergraphs with at most
$|Z_M(\boldsymbol{\lambda })|$
we will use the induction hypotheses (for admissible subhypergraphs with at most
![]() $n$
vertices) to bound
$n$
vertices) to bound
![]() $|Z_{M/v}(\boldsymbol{\lambda })|$
in terms of
$|Z_{M/v}(\boldsymbol{\lambda })|$
in terms of
![]() $|Z_{M-v}(\boldsymbol{\lambda })|$
. Observe that
$|Z_{M-v}(\boldsymbol{\lambda })|$
. Observe that
![]() $M/v$
may be obtained from
$M/v$
may be obtained from
![]() $M-v$
by a sequence of at most
$M-v$
by a sequence of at most
![]() $\Delta$
many vertex deletions and edge additions, and that at each step, we obtain an admissible subhypergraph of
$\Delta$
many vertex deletions and edge additions, and that at each step, we obtain an admissible subhypergraph of
![]() $G$
(allowing us to repeatedly apply the induction hypotheses). More explicitly, beginning with
$G$
(allowing us to repeatedly apply the induction hypotheses). More explicitly, beginning with
![]() $M-v$
, we first delete all 2-neighbours of
$M-v$
, we first delete all 2-neighbours of
![]() $v$
(i.e., vertices
$v$
(i.e., vertices
![]() $u$
such that
$u$
such that
![]() $\{u,v\} \in E_{M-v}$
) to obtain
$\{u,v\} \in E_{M-v}$
) to obtain
![]() $M-(\{v\} \cup C(v))$
, a total of
$M-(\{v\} \cup C(v))$
, a total of
![]() $|C(v)| (=n_{11})$
many applications of vertex deletion. By (2.8), this gives
$|C(v)| (=n_{11})$
many applications of vertex deletion. By (2.8), this gives
Then, to obtain
![]() $M/v$
from
$M/v$
from
![]() $M-(\{v\} \cup C(v))$
, we add a
$M-(\{v\} \cup C(v))$
, we add a
![]() $j$
-edge
$j$
-edge
![]() $A$
for each
$A$
for each
![]() $\{v\} \cup A \in E_M$
for all
$\{v\} \cup A \in E_M$
for all
![]() $j \geq 2$
. (Since
$j \geq 2$
. (Since
![]() $v$
is not a vertex in
$v$
is not a vertex in
![]() $M-(\{v\} \cup C(v))$
, each of these edge additions produces an admissible subhypergraph of
$M-(\{v\} \cup C(v))$
, each of these edge additions produces an admissible subhypergraph of
![]() $G$
). The number of
$G$
). The number of
![]() $j$
-edge additions performed at this step is at most the number of
$j$
-edge additions performed at this step is at most the number of
![]() $(j+1)$
-edges in
$(j+1)$
-edges in
![]() $M$
that include
$M$
that include
![]() $v$
, which recall we have denoted
$v$
, which recall we have denoted
![]() $n_{1j}$
. By (2.9), this gives
$n_{1j}$
. By (2.9), this gives
So combining (2.11) and (2.12), we obtain the following relationship between
![]() $|Z_{M/v}(\boldsymbol{\lambda })|$
and
$|Z_{M/v}(\boldsymbol{\lambda })|$
and
![]() $|Z_{M-v}(\boldsymbol{\lambda })|$
:
$|Z_{M-v}(\boldsymbol{\lambda })|$
:
And combining (2.13) with (2.10), we see that
 \begin{align} |Z_M(\boldsymbol{\lambda })| &\geq |Z_{M-v}(\boldsymbol{\lambda })|\left (1-\frac{R}{\prod _{i\geq 1}(1-s_{i})^{n_{1i}}}\right ). \end{align}
\begin{align} |Z_M(\boldsymbol{\lambda })| &\geq |Z_{M-v}(\boldsymbol{\lambda })|\left (1-\frac{R}{\prod _{i\geq 1}(1-s_{i})^{n_{1i}}}\right ). \end{align}
Thus, our induction hypothesis (2.8) is satisfied for
![]() $M$
(and
$M$
(and
![]() $v$
) as long as the inequality
$v$
) as long as the inequality
 \begin{equation} \left (1-\frac{R}{\prod _{i\geq 1}(1-s_{i})^{n_{1i}}}\right )\geq (1-s_1) \end{equation}
\begin{equation} \left (1-\frac{R}{\prod _{i\geq 1}(1-s_{i})^{n_{1i}}}\right )\geq (1-s_1) \end{equation}
is satisfied, but this is equivalent to (2.6).
Now let us turn to the second part of the induction step, verifying (2.9). Again, let
![]() $M$
be any admissible subhypergraph of
$M$
be any admissible subhypergraph of
![]() $G$
with
$G$
with
![]() $n+1$
vertices and consider any edge
$n+1$
vertices and consider any edge
![]() $\{v_1,\dots,v_{\ell -j},x_1,\dots,x_j\}$
in
$\{v_1,\dots,v_{\ell -j},x_1,\dots,x_j\}$
in
![]() $G$
with
$G$
with
![]() $x_1,\dots,x_j\in V_M$
and
$x_1,\dots,x_j\in V_M$
and
![]() $v_1,\dots,v_{\ell -j}\not \in V_M$
. (So here we are taking
$v_1,\dots,v_{\ell -j}\not \in V_M$
. (So here we are taking
![]() $A=\{x_1,\dots,x_j\}$
; this will be convenient as we will be dealing with the elements of
$A=\{x_1,\dots,x_j\}$
; this will be convenient as we will be dealing with the elements of
![]() $A$
one after another.) First we dispense with a somewhat trivial case: if
$A$
one after another.) First we dispense with a somewhat trivial case: if
![]() $\{x_1,\dots,x_j\}$
contains a hyperedge of
$\{x_1,\dots,x_j\}$
contains a hyperedge of
![]() $M$
then (2.9) is automatically satisfied, since
$M$
then (2.9) is automatically satisfied, since
![]() $Z_M(\boldsymbol{\lambda }) = Z_{M+\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })$
, and so
$Z_M(\boldsymbol{\lambda }) = Z_{M+\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })$
, and so
![]() $|Z_M(\boldsymbol{\lambda })| \geq (1-s_j)\, |Z_{M+\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })|$
for any
$|Z_M(\boldsymbol{\lambda })| \geq (1-s_j)\, |Z_{M+\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })|$
for any
![]() $s_j\in (0,1)$
. So from here on we may assume that no
$s_j\in (0,1)$
. So from here on we may assume that no
![]() $e\in E_M$
is contained in
$e\in E_M$
is contained in
![]() $\{x_1,\dots,x_j\}$
.
$\{x_1,\dots,x_j\}$
.
We begin by applying identity (2.4) to get
As before, using the reverse triangle inequality and noting that
![]() $|\lambda _{x_i}|\leq R$
for all
$|\lambda _{x_i}|\leq R$
for all
![]() $i$
, we obtain
$i$
, we obtain
To obtain a lower bound on
![]() $|Z_M(\boldsymbol{\lambda })|$
, we will apply our induction hypotheses to bound
$|Z_M(\boldsymbol{\lambda })|$
, we will apply our induction hypotheses to bound
![]() $|Z_{M/\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })|$
in terms of
$|Z_{M/\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })|$
in terms of
![]() $|Z_{M+\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })|$
. Notice that
$|Z_{M+\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })|$
. Notice that
![]() $M/\{x_1,\dots,x_j\}$
may be obtained from
$M/\{x_1,\dots,x_j\}$
may be obtained from
![]() $M+\{x_1,\dots,x_j\}$
by the following sequence of steps: Starting from
$M+\{x_1,\dots,x_j\}$
by the following sequence of steps: Starting from
![]() $M+\{x_1,\dots,x_j\}$
, we perform the vertex deletion operation
$M+\{x_1,\dots,x_j\}$
, we perform the vertex deletion operation
![]() $j+|C(\{x_1,\dots,x_j\})| (=n_{j1})$
many times. Then we add (as edges) all the
$j+|C(\{x_1,\dots,x_j\})| (=n_{j1})$
many times. Then we add (as edges) all the
![]() $i$
-sets
$i$
-sets
![]() $\{a_1,\ldots, a_i\}$
such that
$\{a_1,\ldots, a_i\}$
such that
![]() $a_1, \ldots, a_i \in V_M$
and
$a_1, \ldots, a_i \in V_M$
and
![]() $\{x_{k_1},\dots, x_{k_t},a_1,\ldots, a_i\} \in E_M$
for some indices
$\{x_{k_1},\dots, x_{k_t},a_1,\ldots, a_i\} \in E_M$
for some indices
![]() $k_1,\dots, k_t$
; note that there are
$k_1,\dots, k_t$
; note that there are
![]() $n_{ji}$
such
$n_{ji}$
such
![]() $i$
-sets for each possible
$i$
-sets for each possible
![]() $i$
.
$i$
.
Now by (2.8) and (2.9), we have
(Notice that the first application of (2.8) in this sequence is to delete a vertex from
![]() $M+\{x_1,\dots,x_j\}$
, which has
$M+\{x_1,\dots,x_j\}$
, which has
![]() $n+1$
vertices. This is a valid application, since we are assuming the
$n+1$
vertices. This is a valid application, since we are assuming the
![]() $n+1$
case of (2.8) of the induction hypothesis.)
$n+1$
case of (2.8) of the induction hypothesis.)
Combining (2.17) with (2.16) yields
 \begin{align*} |Z_M(\boldsymbol{\lambda })| &\geq |Z_{M+\{x_1,\dots,x_j\}}|\left (1-\frac{R^j}{\prod _{i\geq 1}(1-s_i)^{n_{ji}}}\right ). \end{align*}
\begin{align*} |Z_M(\boldsymbol{\lambda })| &\geq |Z_{M+\{x_1,\dots,x_j\}}|\left (1-\frac{R^j}{\prod _{i\geq 1}(1-s_i)^{n_{ji}}}\right ). \end{align*}
So we obtain (2.9) for
![]() $M$
as long as
$M$
as long as
 \begin{equation*} \left (1-\frac {R^j}{\prod _{i\geq 1}(1-s_i)^{n_{ji}}}\right )\geq (1-s_j), \end{equation*}
\begin{equation*} \left (1-\frac {R^j}{\prod _{i\geq 1}(1-s_i)^{n_{ji}}}\right )\geq (1-s_j), \end{equation*}
which is equivalent to (2.7). This completes the induction.
Remark 11. There is a trick that allows one to replace
![]() $\Delta +1$
by
$\Delta +1$
by
![]() $\Delta$
in the graph case, achieving the optimal bound: by starting from a vertex of degree
$\Delta$
in the graph case, achieving the optimal bound: by starting from a vertex of degree
![]() $\Delta$
, every vertex edited by the subsequent application of the deletion–contraction identity has degree strictly less than
$\Delta$
, every vertex edited by the subsequent application of the deletion–contraction identity has degree strictly less than
![]() $\Delta$
. This is no longer true for hypergraphs. When we start from a vertex of degree
$\Delta$
. This is no longer true for hypergraphs. When we start from a vertex of degree
![]() $\Delta$
, we might keep creating and editing vertices of total degree (or even worse, graph degree)
$\Delta$
, we might keep creating and editing vertices of total degree (or even worse, graph degree)
![]() $\Delta$
. See, however, the improvement achieved in the recent preprint [Reference Bencs and Buys6].
$\Delta$
. See, however, the improvement achieved in the recent preprint [Reference Bencs and Buys6].
3. Linear hypertrees
In the special case of linear hypertrees, we improve the bound in Theorem 8 by using the same inductive argument, but taking into account the special structure of the hypergraphs obtained during the deletion/contraction operations. By choosing the vertex/edge appropriately at each step, we will ensure that the resulting hypergraphs have at most one small (few vertices) edge in every connected component. Since small edges are more ‘costly’ to alter, as we will see below, this will yield the desired improvement in the final bound. The following is the multivariate extension of Theorem 4.
Theorem 12.
For each
![]() $k\geq 3$
, the following holds. For any
$k\geq 3$
, the following holds. For any
![]() $k$
-uniform, linear hypertree
$k$
-uniform, linear hypertree
![]() $G=(V,E)$
with maximum degree
$G=(V,E)$
with maximum degree
![]() $\Delta$
, if
$\Delta$
, if
for all
![]() $v\in V$
, then
$v\in V$
, then
Moreover,
![]() $|\lambda _v| \le \frac{\log 2}{2k} \Delta ^{ - \frac{1}{k-1}}$
implies (
3.1
).
$|\lambda _v| \le \frac{\log 2}{2k} \Delta ^{ - \frac{1}{k-1}}$
implies (
3.1
).
Proof. As in the proof of Theorem 10, we will bound
![]() $|Z_G(\boldsymbol{\lambda })|$
by measuring the effect that removing a single vertex can have on the independence polynomial (and iterating this procedure until we reach the empty graph). In this proof we will carefully control which vertices are removed and which subhypergraphs can be produced as a result. We will first give the precise statements (3.4) and (3.5) that will be proved by induction (which bound the change in the independence polynomial after removing a vertex or adding an edge), before showing how the theorem follows, and finally establishing (3.4) and (3.5).
$|Z_G(\boldsymbol{\lambda })|$
by measuring the effect that removing a single vertex can have on the independence polynomial (and iterating this procedure until we reach the empty graph). In this proof we will carefully control which vertices are removed and which subhypergraphs can be produced as a result. We will first give the precise statements (3.4) and (3.5) that will be proved by induction (which bound the change in the independence polynomial after removing a vertex or adding an edge), before showing how the theorem follows, and finally establishing (3.4) and (3.5).
Let
![]() $M$
be any admissible subhypergraph of
$M$
be any admissible subhypergraph of
![]() $G$
in which every connected component has at most one edge of size strictly less than
$G$
in which every connected component has at most one edge of size strictly less than
![]() $k$
. Let
$k$
. Let
![]() $R\gt 0$
and
$R\gt 0$
and
![]() $s_1,\dots, s_{k-1}\in (0,1)$
be any constants satisfying
$s_1,\dots, s_{k-1}\in (0,1)$
be any constants satisfying
for all
![]() $2\leq j\leq k-2$
, and
$2\leq j\leq k-2$
, and
for all
![]() $2\leq j\leq k-1$
; and let
$2\leq j\leq k-1$
; and let
![]() $\boldsymbol{\lambda }$
satisfy
$\boldsymbol{\lambda }$
satisfy
![]() $|\lambda _v|\leq R$
for all
$|\lambda _v|\leq R$
for all
![]() $v\in V$
. We will inductively prove the following two bounds; notice that both bounds are proved only under careful structural assumptions.
$v\in V$
. We will inductively prove the following two bounds; notice that both bounds are proved only under careful structural assumptions.
-
• First, let
 $v$
be any vertex of
$v$
be any vertex of
 $M$
contained in an edge of size less than
$M$
contained in an edge of size less than
 $k$
, or let
$k$
, or let
 $v$
be any vertex in a connected component of
$v$
be any vertex in a connected component of
 $M$
where all edges have size
$M$
where all edges have size
 $k$
. Then we show that(3.4)
$k$
. Then we show that(3.4) \begin{equation} |Z_M(\boldsymbol{\lambda })|\geq (1-s_1)\,|Z_{M-v}(\boldsymbol{\lambda })|. \end{equation}
\begin{equation} |Z_M(\boldsymbol{\lambda })|\geq (1-s_1)\,|Z_{M-v}(\boldsymbol{\lambda })|. \end{equation}
-
• Second, let
 $2\leq j \leq k-1$
, and let
$2\leq j \leq k-1$
, and let
 $x_1,\dots, x_j$
be any vertices of
$x_1,\dots, x_j$
be any vertices of
 $M$
that are (respectively) in components of
$M$
that are (respectively) in components of
 $M$
where all edges have size
$M$
where all edges have size
 $k$
, and that are in some
$k$
, and that are in some
 $k$
-edge
$k$
-edge
 $\{v_1,\dots, v_{k-j},x_1,\dots, x_j\}$
of
$\{v_1,\dots, v_{k-j},x_1,\dots, x_j\}$
of
 $G$
with
$G$
with
 $v_1,\dots, v_{k-j}\not \in V(M)$
. Then we show that(3.5)
$v_1,\dots, v_{k-j}\not \in V(M)$
. Then we show that(3.5) \begin{equation} |Z_{M}(\boldsymbol{\lambda })|\geq (1-s_j)\,|Z_{M+\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })|. \end{equation}
\begin{equation} |Z_{M}(\boldsymbol{\lambda })|\geq (1-s_j)\,|Z_{M+\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })|. \end{equation}
Before proving (3.4) and (3.5), we show how an iterative application of (3.4) completes the proof of Theorem 12. Let
![]() $\boldsymbol{\lambda }$
be such that
$\boldsymbol{\lambda }$
be such that
![]() $|\lambda _v|\leq R$
for all
$|\lambda _v|\leq R$
for all
![]() $v\in V$
, where
$v\in V$
, where
![]() $R$
and
$R$
and
![]() $s_1,\dots, s_{k-1}$
are any constants satisfying (3.2) and (3.3) above. Taking the vertices of
$s_1,\dots, s_{k-1}$
are any constants satisfying (3.2) and (3.3) above. Taking the vertices of
![]() $G$
in any order
$G$
in any order
![]() $v_1,v_2,\dots, v_{|V|}$
, we write a telescoping product:
$v_1,v_2,\dots, v_{|V|}$
, we write a telescoping product:
 \begin{equation*} |Z_G(\boldsymbol {\lambda })| = \prod _{i=1}^{|V(G)|} \left |\frac {Z_{G-\{v_1, \ldots, v_{i-1}\}}(\boldsymbol {\lambda })}{Z_{G-\{v_1, \ldots, v_i\}}(\boldsymbol {\lambda })}\right |. \end{equation*}
\begin{equation*} |Z_G(\boldsymbol {\lambda })| = \prod _{i=1}^{|V(G)|} \left |\frac {Z_{G-\{v_1, \ldots, v_{i-1}\}}(\boldsymbol {\lambda })}{Z_{G-\{v_1, \ldots, v_i\}}(\boldsymbol {\lambda })}\right |. \end{equation*}
We may then apply (3.4) with
![]() $M = Z_{G-\{v_1, \ldots, v_{i-1}\}}$
and
$M = Z_{G-\{v_1, \ldots, v_{i-1}\}}$
and
![]() $v=v_i$
; notice that these are indeed valid choices respecting our structural constraints, since all edges in
$v=v_i$
; notice that these are indeed valid choices respecting our structural constraints, since all edges in
![]() $Z_{G-\{v_1, \ldots, v_{i-1}\}}$
are of size
$Z_{G-\{v_1, \ldots, v_{i-1}\}}$
are of size
![]() $k$
. Thus, we get the bound
$k$
. Thus, we get the bound
To establish Theorem 12, it remains only to optimise the choice of
![]() $R$
. It would perhaps be difficult to precisely optimise the choices of
$R$
. It would perhaps be difficult to precisely optimise the choices of
![]() $s_1,\dots, s_{k-1}$
to make the bounds (3.2) and (3.3) on
$s_1,\dots, s_{k-1}$
to make the bounds (3.2) and (3.3) on
![]() $R$
as large as possible. But if we take
$R$
as large as possible. But if we take
![]() $s_1=\cdots =s_{k-2} = \Delta ^{-1/(k-1)}$
and
$s_1=\cdots =s_{k-2} = \Delta ^{-1/(k-1)}$
and
![]() $s_{k-1} = 1/\Delta$
, we will be able to choose
$s_{k-1} = 1/\Delta$
, we will be able to choose
![]() $R= \left (\frac{\Delta -1}{\Delta }\right )^{\Delta -1} \left ( 1- \Delta ^{ - \frac{1}{k-1}} \right )\Delta ^{ - \frac{1}{k-1}}$
and ensure that (3.2) and (3.3) are satisfied. Indeed, the constraints are now
$R= \left (\frac{\Delta -1}{\Delta }\right )^{\Delta -1} \left ( 1- \Delta ^{ - \frac{1}{k-1}} \right )\Delta ^{ - \frac{1}{k-1}}$
and ensure that (3.2) and (3.3) are satisfied. Indeed, the constraints are now
and
for all
![]() $2\leq j\leq k-1$
. Note that for
$2\leq j\leq k-1$
. Note that for
![]() $2\leq j\leq k-2$
we have
$2\leq j\leq k-2$
we have
![]() $s_j^{1/j}\lt \Delta ^{- \frac{1}{k-1}}$
, and thus the strongest of these constraints is for
$s_j^{1/j}\lt \Delta ^{- \frac{1}{k-1}}$
, and thus the strongest of these constraints is for
![]() $j=k-1$
, i.e.,
$j=k-1$
, i.e.,
 \begin{align*} R&\leq \Delta ^{ - \frac{1}{k-1}}\cdot \frac{ \Delta ^{ \frac{1}{k-1}}-1}{ \Delta ^{ \frac{1}{k-1}}}\cdot \left (\frac{\Delta -1}{\Delta }\right )^{\Delta -1} \\ &= \left (\frac{\Delta -1}{\Delta }\right )^{\Delta -1} \left ( 1- \Delta ^{ - \frac{1}{k-1}} \right )\Delta ^{ - \frac{1}{k-1}}. \end{align*}
\begin{align*} R&\leq \Delta ^{ - \frac{1}{k-1}}\cdot \frac{ \Delta ^{ \frac{1}{k-1}}-1}{ \Delta ^{ \frac{1}{k-1}}}\cdot \left (\frac{\Delta -1}{\Delta }\right )^{\Delta -1} \\ &= \left (\frac{\Delta -1}{\Delta }\right )^{\Delta -1} \left ( 1- \Delta ^{ - \frac{1}{k-1}} \right )\Delta ^{ - \frac{1}{k-1}}. \end{align*}
It is now easy to see that the above bound is lower than the one in (3.2), so we may chose
![]() $R$
to be equal to this value. Thus if
$R$
to be equal to this value. Thus if
![]() $|\lambda _v|\leq R = \left (\frac{\Delta -1}{\Delta }\right )^{\Delta -1} \left ( 1- \Delta ^{ - \frac{1}{k-1}} \right )\Delta ^{ - \frac{1}{k-1}}$
for all
$|\lambda _v|\leq R = \left (\frac{\Delta -1}{\Delta }\right )^{\Delta -1} \left ( 1- \Delta ^{ - \frac{1}{k-1}} \right )\Delta ^{ - \frac{1}{k-1}}$
for all
![]() $v\in V$
, then
$v\in V$
, then
finishing the proof of Theorem 12. Note also that the factor
![]() $\left (\frac{\Delta -1}{\Delta }\right )^{\Delta -1} \left ( 1- \Delta ^{ - \frac{1}{k-1}} \right )$
is increasing in
$\left (\frac{\Delta -1}{\Delta }\right )^{\Delta -1} \left ( 1- \Delta ^{ - \frac{1}{k-1}} \right )$
is increasing in
![]() $\Delta$
and
$\Delta$
and
![]() $\left (\frac{\Delta -1}{\Delta }\right )^{\Delta -1} \left ( 1- \Delta ^{ - \frac{1}{k-1}} \right )\cdot k$
is decreasing in
$\left (\frac{\Delta -1}{\Delta }\right )^{\Delta -1} \left ( 1- \Delta ^{ - \frac{1}{k-1}} \right )\cdot k$
is decreasing in
![]() $k$
, so to obtain the conclusion it suffices that
$k$
, so to obtain the conclusion it suffices that
![]() $|\lambda _v| \le \frac{\log 2}{2k} \Delta ^{ - \frac{1}{k-1}}$
, since
$|\lambda _v| \le \frac{\log 2}{2k} \Delta ^{ - \frac{1}{k-1}}$
, since
![]() $\lim _{k \to \infty } k(1-2^{-1/(k-1)}) = \log 2$
.
$\lim _{k \to \infty } k(1-2^{-1/(k-1)}) = \log 2$
.
We now return to the vertex and edge deletion bounds (3.4) and (3.5), which we will prove by induction. The base case is
![]() $M=\varnothing$
, where both (3.4) and (3.5) are vacuously true.
$M=\varnothing$
, where both (3.4) and (3.5) are vacuously true.
For the induction step, assume that (3.4) and (3.5) hold for all
![]() $M$
with
$M$
with
![]() $|V(M)|\leq n$
, and consider any admissible subhypergraph
$|V(M)|\leq n$
, and consider any admissible subhypergraph
![]() $\Lambda$
of
$\Lambda$
of
![]() $G$
with
$G$
with
![]() $n+1$
vertices, where
$n+1$
vertices, where
![]() $\Lambda$
satisfies the assumption that every connected component has at most one edge of size strictly less than
$\Lambda$
satisfies the assumption that every connected component has at most one edge of size strictly less than
![]() $k$
.
$k$
.
We first establish (3.4) for
![]() $\Lambda$
. To that end, let
$\Lambda$
. To that end, let
![]() $v$
be any vertex of
$v$
be any vertex of
![]() $\Lambda$
satisfying the hypotheses of (3.4). To bound
$\Lambda$
satisfying the hypotheses of (3.4). To bound
![]() $|Z_\Lambda (\boldsymbol{\lambda })|$
, we begin by applying identity (2.3):
$|Z_\Lambda (\boldsymbol{\lambda })|$
, we begin by applying identity (2.3):
And using the reverse triangle inequality and noting that
![]() $|\lambda _v|\leq R$
by assumption, this gives
$|\lambda _v|\leq R$
by assumption, this gives
To extract the desired lower bound on
![]() $|Z_\Lambda (\boldsymbol{\lambda })|$
, we will use our induction hypotheses to bound
$|Z_\Lambda (\boldsymbol{\lambda })|$
, we will use our induction hypotheses to bound
![]() $|Z_{\Lambda/v}(\boldsymbol{\lambda })|$
in terms of
$|Z_{\Lambda/v}(\boldsymbol{\lambda })|$
in terms of
![]() $|Z_{\Lambda -v}(\boldsymbol{\lambda })|$
. Observe that
$|Z_{\Lambda -v}(\boldsymbol{\lambda })|$
. Observe that
![]() $\Lambda/v$
may be obtained from
$\Lambda/v$
may be obtained from
![]() $\Lambda -v$
by a sequence of at most
$\Lambda -v$
by a sequence of at most
![]() $\Delta$
many vertex deletions and
$\Delta$
many vertex deletions and
![]() $j$
-edge additions (for
$j$
-edge additions (for
![]() $2\leq j\leq k-1$
). But we must take care to verify that at each step, all the necessary conditions are satisfied to apply the induction hypotheses.
$2\leq j\leq k-1$
). But we must take care to verify that at each step, all the necessary conditions are satisfied to apply the induction hypotheses.
First, if
![]() $v$
is contained in a 2-edge
$v$
is contained in a 2-edge
![]() $\{v,x\}$
of
$\{v,x\}$
of
![]() $\Lambda$
, then starting from
$\Lambda$
, then starting from
![]() $\Lambda -v$
, we delete
$\Lambda -v$
, we delete
![]() $x$
. (Notice that by assumption,
$x$
. (Notice that by assumption,
![]() $v$
is contained in at most one such edge.) And we can indeed apply hypothesis (3.4) (with
$v$
is contained in at most one such edge.) And we can indeed apply hypothesis (3.4) (with
![]() $M=\Lambda -v$
), as
$M=\Lambda -v$
), as
![]() $\Lambda -v$
has at most one edge of size less than
$\Lambda -v$
has at most one edge of size less than
![]() $k$
in each connected component, and
$k$
in each connected component, and
![]() $x$
is in a component of
$x$
is in a component of
![]() $\Lambda -v$
where all edges have size
$\Lambda -v$
where all edges have size
![]() $k$
(the edge
$k$
(the edge
![]() $\{v,x\}$
is excluded from
$\{v,x\}$
is excluded from
![]() $\Lambda -v$
). So applying (3.4), this gives
$\Lambda -v$
). So applying (3.4), this gives
if
![]() $v$
has a graph neighbour
$v$
has a graph neighbour
![]() $x$
.
$x$
.
Then, regardless of whether
![]() $v$
is contained in a 2-edge, to obtain
$v$
is contained in a 2-edge, to obtain
![]() $\Lambda/v$
from
$\Lambda/v$
from
![]() $\Lambda -v-N_2(v)$
, we add a
$\Lambda -v-N_2(v)$
, we add a
![]() $j$
-edge
$j$
-edge
![]() $\{x_1,\dots,x_j\}$
for each
$\{x_1,\dots,x_j\}$
for each
![]() $\{v,x_1,\dots,x_j\}\in E(\Lambda )$
, for all
$\{v,x_1,\dots,x_j\}\in E(\Lambda )$
, for all
![]() $2\leq j\leq k-1$
.
$2\leq j\leq k-1$
.
The number of
![]() $j$
-edge additions performed at this step is at most the number of
$j$
-edge additions performed at this step is at most the number of
![]() $(j+1)$
-edges in
$(j+1)$
-edges in
![]() $\Lambda$
adjacent to
$\Lambda$
adjacent to
![]() $v$
, which we will denote
$v$
, which we will denote
![]() $n_{1j}$
. Note that most of the numbers
$n_{1j}$
. Note that most of the numbers
![]() $n_{1j}$
will be zero, as
$n_{1j}$
will be zero, as
![]() $v$
is adjacent to at most one edge of size less than
$v$
is adjacent to at most one edge of size less than
![]() $k$
.
$k$
.
And we may indeed apply induction hypothesis (3.5) for these edge additions: regardless of the order in which we add these edges, at each step, the corresponding
![]() $x_1,\dots,x_j$
are in different components from any edges of size less than
$x_1,\dots,x_j$
are in different components from any edges of size less than
![]() $k$
added at previous steps, since the vertex
$k$
added at previous steps, since the vertex
![]() $v$
is no longer present. And at each step, the hypergraph produced has at most one edge of size less than
$v$
is no longer present. And at each step, the hypergraph produced has at most one edge of size less than
![]() $k$
in each connected component. So we may repeatedly apply our second induction hypothesis (3.5) to obtain
$k$
in each connected component. So we may repeatedly apply our second induction hypothesis (3.5) to obtain
Then combining (3.7) and (3.8), we obtain the following relationship between
![]() $|Z_{\Lambda/v}(\boldsymbol{\lambda })|$
and
$|Z_{\Lambda/v}(\boldsymbol{\lambda })|$
and
![]() $|Z_{\Lambda -v}(\boldsymbol{\lambda })|$
:
$|Z_{\Lambda -v}(\boldsymbol{\lambda })|$
:
(where
![]() $n_{1i}$
is the number of graph neighbours of
$n_{1i}$
is the number of graph neighbours of
![]() $v$
, which is either 0 or 1). And notice that, since
$v$
, which is either 0 or 1). And notice that, since
![]() $v$
is contained in at most one edge of size less than
$v$
is contained in at most one edge of size less than
![]() $k$
, and at most
$k$
, and at most
![]() $\Delta$
edges total, this bound may be simplified substantially:
$\Delta$
edges total, this bound may be simplified substantially:
for some
![]() $1\leq j\leq k-2$
. (Note: we may very slightly improve this bound by considering whether or not
$1\leq j\leq k-2$
. (Note: we may very slightly improve this bound by considering whether or not
![]() $v$
is contained in an edge of size less than
$v$
is contained in an edge of size less than
![]() $k$
, but this will not substantially change our final answer. Also, we cannot control which
$k$
, but this will not substantially change our final answer. Also, we cannot control which
![]() $j$
is used; we must simply take the worst case.)
$j$
is used; we must simply take the worst case.)
And combining this with (3.6), we see that
 \begin{align*} |Z_\Lambda (\boldsymbol{\lambda })| &\geq |Z_{\Lambda -v}(\boldsymbol{\lambda })|\left (1-R\left (\frac{1}{1-s_j}\right )\left (\frac{1}{1-s_{k-1}}\right )^{\Delta }\right ). \end{align*}
\begin{align*} |Z_\Lambda (\boldsymbol{\lambda })| &\geq |Z_{\Lambda -v}(\boldsymbol{\lambda })|\left (1-R\left (\frac{1}{1-s_j}\right )\left (\frac{1}{1-s_{k-1}}\right )^{\Delta }\right ). \end{align*}
for all
![]() $1\leq j\leq k-2$
. Thus the induction hypothesis (3.4) is guaranteed to be satisfied for
$1\leq j\leq k-2$
. Thus the induction hypothesis (3.4) is guaranteed to be satisfied for
![]() $\Lambda$
as long as
$\Lambda$
as long as
for each
![]() $1\leq j\leq k-2$
; this is equivalent to condition (3.2) above.
$1\leq j\leq k-2$
; this is equivalent to condition (3.2) above.
We now proceed with the induction step for (3.5), which deals with edge addition. Again, we let
![]() $\Lambda$
be any admissible subhypergraph of
$\Lambda$
be any admissible subhypergraph of
![]() $G$
with
$G$
with
![]() $n+1$
vertices satisfying the assumption that every connected component has at most one edge of size strictly less than
$n+1$
vertices satisfying the assumption that every connected component has at most one edge of size strictly less than
![]() $k$
. Let
$k$
. Let
![]() $2\leq j\leq k-1$
, and consider any
$2\leq j\leq k-1$
, and consider any
![]() $x_1,\dots, x_j$
in
$x_1,\dots, x_j$
in
![]() $\Lambda$
satisfying the hypotheses of (3.5) – that is, that
$\Lambda$
satisfying the hypotheses of (3.5) – that is, that
![]() $x_1,\dots, x_j$
are (respectively) in components of
$x_1,\dots, x_j$
are (respectively) in components of
![]() $\Lambda$
where all edges have size
$\Lambda$
where all edges have size
![]() $k$
, and they are in some
$k$
, and they are in some
![]() $k$
-edge
$k$
-edge
![]() $\{v_1,\dots, v_{k-j},x_1,\dots, x_j\}$
of
$\{v_1,\dots, v_{k-j},x_1,\dots, x_j\}$
of
![]() $G$
with
$G$
with
![]() $v_1,\dots, v_{k-j}\not \in V(\Lambda )$
. Notice that this implies
$v_1,\dots, v_{k-j}\not \in V(\Lambda )$
. Notice that this implies
![]() $\Lambda + \{x_1,\dots,x_j\}$
is also an admissible subhypergraph of
$\Lambda + \{x_1,\dots,x_j\}$
is also an admissible subhypergraph of
![]() $G$
, and that each component has at most one edge of size less than
$G$
, and that each component has at most one edge of size less than
![]() $k$
(the setting of our induction hypotheses).
$k$
(the setting of our induction hypotheses).
To bound
![]() $|Z_{\Lambda +\{x_1,\dots,x_j\}}|$
, we begin by applying identity (2.4):
$|Z_{\Lambda +\{x_1,\dots,x_j\}}|$
, we begin by applying identity (2.4):
Then as above, by using the reverse triangle inequality and noting that
![]() $|\lambda _{x_1}|,\dots, |\lambda _{x_j}|\leq R$
, we obtain
$|\lambda _{x_1}|,\dots, |\lambda _{x_j}|\leq R$
, we obtain
To obtain a lower bound on
![]() $|Z_\Lambda (\boldsymbol{\lambda })|$
, we will apply our induction hypotheses to bound
$|Z_\Lambda (\boldsymbol{\lambda })|$
, we will apply our induction hypotheses to bound
![]() $|Z_{\Lambda/\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })|$
in terms of
$|Z_{\Lambda/\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })|$
in terms of
![]() $|Z_{\Lambda +\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })|$
. Notice that
$|Z_{\Lambda +\{x_1,\dots,x_j\}}(\boldsymbol{\lambda })|$
. Notice that
![]() $\Lambda/\{x_1,\dots,x_j\}$
may be obtained from
$\Lambda/\{x_1,\dots,x_j\}$
may be obtained from
![]() $\Lambda +\{x_1,\dots,x_j\}$
by a sequence of at most
$\Lambda +\{x_1,\dots,x_j\}$
by a sequence of at most
![]() $j\Delta$
many operations as follows: first, we delete
$j\Delta$
many operations as follows: first, we delete
![]() $x_1, x_2,\dots,$
and
$x_1, x_2,\dots,$
and
![]() $x_j$
. Note that, unlike in the general case, we do not need to delete
$x_j$
. Note that, unlike in the general case, we do not need to delete
![]() $C(x_1,\dots, x_j)$
; by our assumptions, this set is empty. Then add each
$C(x_1,\dots, x_j)$
; by our assumptions, this set is empty. Then add each
![]() $(k-1)$
-edge
$(k-1)$
-edge
![]() $\{y_1,\dots, y_{k-1}\}$
where
$\{y_1,\dots, y_{k-1}\}$
where
![]() $\{x_i,y_1,\dots, y_{k-1}\}$
is in
$\{x_i,y_1,\dots, y_{k-1}\}$
is in
![]() $E(\Lambda )$
for some
$E(\Lambda )$
for some
![]() $x_i$
.
$x_i$
.
In total, starting from
![]() $\Lambda +\{x_1,\dots,x_j\}$
, we perform the vertex deletion operation
$\Lambda +\{x_1,\dots,x_j\}$
, we perform the vertex deletion operation
![]() $j$
times, and the
$j$
times, and the
![]() $(k-1)$
-edge addition operation at most
$(k-1)$
-edge addition operation at most
![]() $j(\Delta -1)$
many times – once for each of the
$j(\Delta -1)$
many times – once for each of the
![]() $\leq \Delta -1$
edges adjacent to
$\leq \Delta -1$
edges adjacent to
![]() $x_1,\dots, x_j$
in
$x_1,\dots, x_j$
in
![]() $\Lambda + \{x_1,\dots,x_j\}$
respectively (excluding the edge
$\Lambda + \{x_1,\dots,x_j\}$
respectively (excluding the edge
![]() $\{x_1,\dots,x_j\}$
). And again, we must take care to verify that at each step, all the necessary conditions to apply (3.4) and (3.5) are satisfied.
$\{x_1,\dots,x_j\}$
). And again, we must take care to verify that at each step, all the necessary conditions to apply (3.4) and (3.5) are satisfied.
First, notice that our initial application of (3.4) in this sequence is to delete a vertex from
![]() $\Lambda + \{x_1,\dots,x_j\}$
, which has
$\Lambda + \{x_1,\dots,x_j\}$
, which has
![]() $n+1$
vertices. We are allowed to do so, since we just established the
$n+1$
vertices. We are allowed to do so, since we just established the
![]() $n+1$
case of (3.4) above, and, without loss of generality, we begin by deleting the vertex
$n+1$
case of (3.4) above, and, without loss of generality, we begin by deleting the vertex
![]() $x_1$
, which is contained in an edge of size
$x_1$
, which is contained in an edge of size
![]() $j\lt k$
in
$j\lt k$
in
![]() $\Lambda + \{x_1,\dots,x_j\}$
. We may also delete
$\Lambda + \{x_1,\dots,x_j\}$
. We may also delete
![]() $x_2,\dots, x_j$
next, as vertices in components where all edges have size
$x_2,\dots, x_j$
next, as vertices in components where all edges have size
![]() $k$
. Furthermore, at each step, regardless of the order in which we add the
$k$
. Furthermore, at each step, regardless of the order in which we add the
![]() $(k-1)$
-edges
$(k-1)$
-edges
![]() $\{y_1,\dots, y_{k-1}\}$
, the corresponding
$\{y_1,\dots, y_{k-1}\}$
, the corresponding
![]() $y_1,\dots, y_{k-1}$
are in different components from any
$y_1,\dots, y_{k-1}$
are in different components from any
![]() $(k-1)$
-edges added at previous steps, since
$(k-1)$
-edges added at previous steps, since
![]() $x_1,\dots,x_j$
are no longer present. Finally, at each step, the hypergraph produced has at most one edge of size less than
$x_1,\dots,x_j$
are no longer present. Finally, at each step, the hypergraph produced has at most one edge of size less than
![]() $k$
in each connected component.
$k$
in each connected component.
Now, combining this inequality with (3.11), we see that
 \begin{align*} |Z_\Lambda (\boldsymbol{\lambda })| &\geq |Z_{\Lambda +\{x_1,\dots,x_j\}}|\left (1-R^ j\left (\frac{1}{1-s_1}\right )^{j}\left (\frac{1}{1-s_{k-1}}\right )^{j(\Delta -1)}\right ). \end{align*}
\begin{align*} |Z_\Lambda (\boldsymbol{\lambda })| &\geq |Z_{\Lambda +\{x_1,\dots,x_j\}}|\left (1-R^ j\left (\frac{1}{1-s_1}\right )^{j}\left (\frac{1}{1-s_{k-1}}\right )^{j(\Delta -1)}\right ). \end{align*}
So we will obtain (3.5) for
![]() $\Lambda$
as long as
$\Lambda$
as long as
for each
![]() $2\leq j\leq k-1$
; this is equivalent to condition (3.3) above.
$2\leq j\leq k-1$
; this is equivalent to condition (3.3) above.
Therefore, if conditions (3.3) and (3.3) are satisfied, this completes the induction, giving the edge and vertex deletion bounds (3.4) and (3.5), as desired.
4. Constructions
In this section we provide the constructions that prove Propositions 2 and 5.
4.1 An odd construction (due to Wojciech Samotij)
Here we describe, for each odd
![]() $k \geq 3$
a
$k \geq 3$
a
![]() $k$
-uniform hypergraph
$k$
-uniform hypergraph
![]() $H_{k,\Delta }$
with maximum degree
$H_{k,\Delta }$
with maximum degree
![]() $\Delta =(k-1)s$
for all large enough positive integers
$\Delta =(k-1)s$
for all large enough positive integers
![]() $s=s(k)$
with the following property: the univariate independence polynomial
$s=s(k)$
with the following property: the univariate independence polynomial
![]() $Z_{H_{k,\Delta }}(\lambda )$
of
$Z_{H_{k,\Delta }}(\lambda )$
of
![]() $H_{k,\Delta }$
is negative at
$H_{k,\Delta }$
is negative at
![]() $x=-k(\log \Delta )/\Delta$
. In particular, since
$x=-k(\log \Delta )/\Delta$
. In particular, since
![]() $Z_{H_{k,\Delta }}(\lambda )\ge 1$
for
$Z_{H_{k,\Delta }}(\lambda )\ge 1$
for
![]() $\lambda \ge 0$
, there must be some
$\lambda \ge 0$
, there must be some
![]() $\lambda \lt 0$
,
$\lambda \lt 0$
,
![]() $|\lambda | \lt k(\log \Delta )/\Delta$
so that
$|\lambda | \lt k(\log \Delta )/\Delta$
so that
![]() $Z_{H_{k,\Delta }}(\lambda ) =0$
. This will prove Proposition 2.
$Z_{H_{k,\Delta }}(\lambda ) =0$
. This will prove Proposition 2.
The vertex set of
![]() $H_{k,\Delta }$
consists of a set
$H_{k,\Delta }$
consists of a set
![]() $\{x_1, \ldots, x_k\}$
, together with, for each
$\{x_1, \ldots, x_k\}$
, together with, for each
![]() $i=1, \ldots, k$
, a set
$i=1, \ldots, k$
, a set
![]() $\{y^i_1, \ldots, y^i_s\}$
, where
$\{y^i_1, \ldots, y^i_s\}$
, where
![]() $s$
will be chosen later to be large enough. For each
$s$
will be chosen later to be large enough. For each
![]() $i=1, \ldots, k$
and each
$i=1, \ldots, k$
and each
![]() $j=1, \ldots, s$
there is an edge
$j=1, \ldots, s$
there is an edge
![]() $(\{x_1, \ldots, x_k\}\setminus \{x_i\}) \cup y^i_j$
.
$(\{x_1, \ldots, x_k\}\setminus \{x_i\}) \cup y^i_j$
.
In other words, we start with a set
![]() $R$
of
$R$
of
![]() $k$
vertices, and to each
$k$
vertices, and to each
![]() $(k-1)$
-subset
$(k-1)$
-subset
![]() $R'$
of
$R'$
of
![]() $R$
we associate a cloud
$R$
we associate a cloud
![]() $C(R')$
of
$C(R')$
of
![]() $s$
vertices. An edge is formed by taking an
$s$
vertices. An edge is formed by taking an
![]() $R'$
together with one element from its cloud
$R'$
together with one element from its cloud
![]() $C(R')$
.
$C(R')$
.
Each
![]() $x_i$
is in
$x_i$
is in
![]() $k-1$
$k-1$
![]() $(k-1)$
-subsets of
$(k-1)$
-subsets of
![]() $\{x_1, \ldots, x_k\}$
, and each such subset can be extended to an edge of
$\{x_1, \ldots, x_k\}$
, and each such subset can be extended to an edge of
![]() $H_{k,\Delta }$
in
$H_{k,\Delta }$
in
![]() $s$
ways, so the degree of each
$s$
ways, so the degree of each
![]() $x_i$
is
$x_i$
is
![]() $(k-1)s$
. Each
$(k-1)s$
. Each
![]() $y^i_j$
has degree 1. So the maximum degree of
$y^i_j$
has degree 1. So the maximum degree of
![]() $H_{k,\Delta }$
is
$H_{k,\Delta }$
is
![]() $\Delta :\!=(k-1)s$
.
$\Delta :\!=(k-1)s$
.
For each
![]() $0 \leq \ell \lt k-1$
, the total contribution to
$0 \leq \ell \lt k-1$
, the total contribution to
![]() $Z_{H_{k,\Delta }}(\lambda )$
from independent sets that use exactly
$Z_{H_{k,\Delta }}(\lambda )$
from independent sets that use exactly
![]() $\ell$
vertices from
$\ell$
vertices from
![]() $\{x_1, \ldots, x_k\}$
is
$\{x_1, \ldots, x_k\}$
is
Since
![]() $\ell \lt k-1$
, an arbitrary subset of the
$\ell \lt k-1$
, an arbitrary subset of the
![]() $y^i_j$
can be added to any
$y^i_j$
can be added to any
![]() $\ell$
-subset of
$\ell$
-subset of
![]() $\{x_1, \ldots, x_\ell \}$
without saturating an edge of
$\{x_1, \ldots, x_\ell \}$
without saturating an edge of
![]() $H_{k,\Delta }$
. The total contribution to
$H_{k,\Delta }$
. The total contribution to
![]() $Z_{H_{k,\Delta }}(\lambda )$
from independent sets that use exactly
$Z_{H_{k,\Delta }}(\lambda )$
from independent sets that use exactly
![]() $k-1$
vertices from
$k-1$
vertices from
![]() $\{x_1, \ldots, x_k\}$
is
$\{x_1, \ldots, x_k\}$
is
If
![]() $x_i$
is the one vertex from
$x_i$
is the one vertex from
![]() $\{x_1, \ldots, x_\ell \}$
not selected, then no
$\{x_1, \ldots, x_\ell \}$
not selected, then no
![]() $x^i_j$
can be added without saturating an edge, but any subset of the
$x^i_j$
can be added without saturating an edge, but any subset of the
![]() $x^{i'}_j$
for
$x^{i'}_j$
for
![]() $i' \neq i$
can be. Finally, the contribution to
$i' \neq i$
can be. Finally, the contribution to
![]() $Z_{H_{k,\Delta }}(\lambda )$
from independent sets that use all of
$Z_{H_{k,\Delta }}(\lambda )$
from independent sets that use all of
![]() $\{x_1, \ldots, x_k\}$
is simply
$\{x_1, \ldots, x_k\}$
is simply
![]() $\lambda ^k$
(no extra vertices can be added without saturating an edge).
$\lambda ^k$
(no extra vertices can be added without saturating an edge).
We now specialise to
![]() $\lambda =-k(\log \Delta )/\Delta$
. Recalling
$\lambda =-k(\log \Delta )/\Delta$
. Recalling
![]() $\Delta =(k-1)s$
, where
$\Delta =(k-1)s$
, where
![]() $s$
is large enough so that
$s$
is large enough so that
![]() $\lambda \geq -1$
, and using that
$\lambda \geq -1$
, and using that
![]() $0\leq 1+t \leq e^t$
for all
$0\leq 1+t \leq e^t$
for all
![]() $t\geq -1$
, we get that for
$t\geq -1$
, we get that for
![]() $\ell \lt k-1$
,
$\ell \lt k-1$
,
and
where
![]() $c(k)$
is a constant depending only on
$c(k)$
is a constant depending only on
![]() $k$
.
$k$
.
On the other hand, we have
(note that we use here that
![]() $k$
is odd). Because
$k$
is odd). Because
![]() $k \lt 2k-1$
and
$k \lt 2k-1$
and
![]() $k \lt \ell +k^2/(k-1)$
for all
$k \lt \ell +k^2/(k-1)$
for all
![]() $\ell \lt k-1$
, we have that for all sufficiently large
$\ell \lt k-1$
, we have that for all sufficiently large
![]() $s=s(k)$
,
$s=s(k)$
,
 \begin{equation*} k^k\frac {(\log (k-1)s)^k}{s^k} \gt c(k)\left (\frac {(\log (k-1)s)^{k-1}}{s^{2k-1}} + \sum _{\ell =0}^{k-2} \frac {(\log (k-1)s)^\ell }{s^{\ell +\frac {k^2}{k-1}}}\right ) \end{equation*}
\begin{equation*} k^k\frac {(\log (k-1)s)^k}{s^k} \gt c(k)\left (\frac {(\log (k-1)s)^{k-1}}{s^{2k-1}} + \sum _{\ell =0}^{k-2} \frac {(\log (k-1)s)^\ell }{s^{\ell +\frac {k^2}{k-1}}}\right ) \end{equation*}
and so
![]() $Z_{H_{k,\Delta }}(\lambda )\lt 0$
at
$Z_{H_{k,\Delta }}(\lambda )\lt 0$
at
![]() $x=-k(\log \Delta )/\Delta$
, as claimed.
$x=-k(\log \Delta )/\Delta$
, as claimed.
4.2 An even construction (due to the anonymous referee)
For even
![]() $k$
, consider a hypergraph with
$k$
, consider a hypergraph with
![]() $\Delta$
edges that has
$\Delta$
edges that has
![]() $k-1$
common vertices, i.e., let
$k-1$
common vertices, i.e., let
![]() $x_1, \ldots, x_{k-1}, y_1, \ldots, y_{\Delta }$
be the vertex set and
$x_1, \ldots, x_{k-1}, y_1, \ldots, y_{\Delta }$
be the vertex set and
![]() $\left \{\left \{x_1, \ldots, x_{k-1}, y_i\right \}\right .$
for
$\left \{\left \{x_1, \ldots, x_{k-1}, y_i\right \}\right .$
for
![]() $\left .i=1, \ldots, \Delta \right \}$
the edge set. Then the independence polynomial is
$\left .i=1, \ldots, \Delta \right \}$
the edge set. Then the independence polynomial is
Let
![]() $\lambda =-\frac{(k-1) \log \Delta }{\Delta }$
, with
$\lambda =-\frac{(k-1) \log \Delta }{\Delta }$
, with
![]() $\Delta$
taken large enough that
$\Delta$
taken large enough that
![]() $\lambda \ge -1$
. Then,
$\lambda \ge -1$
. Then,
and for even
![]() $k$
we have
$k$
we have
 \begin{equation*} \left (1-\left (1-\frac {(k-1) \log \Delta }{\Delta }\right )^{\Delta }\right )\left (-\frac {(k-1) \log \Delta }{\Delta }\right )^{k-1}\lt -\left (1-\Delta ^{-(k-1)}\right )\left (\frac {(k-1) \log \Delta }{\Delta }\right )^{k-1} \end{equation*}
\begin{equation*} \left (1-\left (1-\frac {(k-1) \log \Delta }{\Delta }\right )^{\Delta }\right )\left (-\frac {(k-1) \log \Delta }{\Delta }\right )^{k-1}\lt -\left (1-\Delta ^{-(k-1)}\right )\left (\frac {(k-1) \log \Delta }{\Delta }\right )^{k-1} \end{equation*}
So we only need that
![]() $\left (1-\Delta ^{-(k-1)}\right )((k-1) \log \Delta )^{k-1} \geq 1$
to conclude that the independence polynomial has a zero of absolute value at most
$\left (1-\Delta ^{-(k-1)}\right )((k-1) \log \Delta )^{k-1} \geq 1$
to conclude that the independence polynomial has a zero of absolute value at most
![]() $\frac{(k-1) \log \Delta }{\Delta }$
.
$\frac{(k-1) \log \Delta }{\Delta }$
.
4.3 A hypertree construction
We now give a construction to prove Proposition 5 and show that the bound in Theorem 12 cannot be improved beyond a polylogarithmic factor in
![]() $\Delta$
.
$\Delta$
.
Consider the
![]() $k$
-uniform star of size
$k$
-uniform star of size
![]() $\Delta$
,
$\Delta$
,
![]() $S^k_\Delta$
, which consists of
$S^k_\Delta$
, which consists of
![]() $\Delta$
edges (each of size
$\Delta$
edges (each of size
![]() $k$
) that share a single vertex, so
$k$
) that share a single vertex, so
![]() $S^k_\Delta$
has
$S^k_\Delta$
has
![]() $1+(k-1)\Delta$
vertices in total. The independence polynomial of
$1+(k-1)\Delta$
vertices in total. The independence polynomial of
![]() $S^k_\Delta$
is
$S^k_\Delta$
is
Let
![]() $k$
be even. We will prove that
$k$
be even. We will prove that
![]() $Z_{S^k_\Delta }\left (-C\left (\frac{\log \Delta }{\Delta }\right )^{1/(k-1)}\right )\lt 0$
for a constant
$Z_{S^k_\Delta }\left (-C\left (\frac{\log \Delta }{\Delta }\right )^{1/(k-1)}\right )\lt 0$
for a constant
![]() $C$
and
$C$
and
![]() $\Delta$
large enough, and thus
$\Delta$
large enough, and thus
![]() $Z_S$
will have a root of magnitude at most
$Z_S$
will have a root of magnitude at most
![]() $C\left (\frac{\log \Delta }{\Delta }\right )^{1/(k-1)}$
.
$C\left (\frac{\log \Delta }{\Delta }\right )^{1/(k-1)}$
.
Note that the
![]() $\lambda$
we choose will clearly satisfy
$\lambda$
we choose will clearly satisfy
![]() $|\lambda |\lt 1$
so it is equivalent to show
$|\lambda |\lt 1$
so it is equivalent to show
 \begin{equation*}1+\lambda \left (1-\left (\frac {\lambda }{1+\lambda }\right )^{k-1}\right )^{\Delta }\lt 0.\end{equation*}
\begin{equation*}1+\lambda \left (1-\left (\frac {\lambda }{1+\lambda }\right )^{k-1}\right )^{\Delta }\lt 0.\end{equation*}
Let
![]() $\frac{\lambda }{1+\lambda }=-f(\Delta )$
, so that
$\frac{\lambda }{1+\lambda }=-f(\Delta )$
, so that
![]() $\lambda = -\frac{f(\Delta )}{1+f(\Delta )}.$
When
$\lambda = -\frac{f(\Delta )}{1+f(\Delta )}.$
When
![]() $k$
is even, we can rewrite the expression as
$k$
is even, we can rewrite the expression as
Set
![]() $f(\Delta ):\!=(\log \Delta/\Delta )^{1/(k-1)}$
, and then the asymptotic behaviour of the above expression is
$f(\Delta ):\!=(\log \Delta/\Delta )^{1/(k-1)}$
, and then the asymptotic behaviour of the above expression is
Note that for this
![]() $f(\Delta )$
, we have
$f(\Delta )$
, we have
![]() $|\lambda |=\Theta \left (|f(\Delta )|\right )=\Theta \left (\left (\frac{\log \Delta }{\Delta }\right )^{1/(k-1)}\right ).$
$|\lambda |=\Theta \left (|f(\Delta )|\right )=\Theta \left (\left (\frac{\log \Delta }{\Delta }\right )^{1/(k-1)}\right ).$
5. Algorithms
Given the zero-freeness result of Theorem 1, we can obtain an FPTAS for
![]() $Z_G(\lambda )$
and prove Theorem 9 following Barvinok’s method of polynomial interpolation: truncating the Taylor series for
$Z_G(\lambda )$
and prove Theorem 9 following Barvinok’s method of polynomial interpolation: truncating the Taylor series for
![]() $\log Z_G(\lambda )$
(in fact, the cluster expansion) around
$\log Z_G(\lambda )$
(in fact, the cluster expansion) around
![]() $0$
after a given number of terms. This approach has been used in several recent works on approximate counting, including [Reference Bencs and Csikvári8, Reference Bezáková, Galanis, Goldberg and Stefankovic13, Reference de Boer, Buys, Guerini, Peters and Regts22, Reference Helmuth, Perkins and Regts33, Reference Patel and Regts47, Reference Peters and Regts49] on approximating the independence polynomial of bounded-degree graphs for (possibly complex) values of
$0$
after a given number of terms. This approach has been used in several recent works on approximate counting, including [Reference Bencs and Csikvári8, Reference Bezáková, Galanis, Goldberg and Stefankovic13, Reference de Boer, Buys, Guerini, Peters and Regts22, Reference Helmuth, Perkins and Regts33, Reference Patel and Regts47, Reference Peters and Regts49] on approximating the independence polynomial of bounded-degree graphs for (possibly complex) values of
![]() $\lambda$
.
$\lambda$
.
Restating Theorem 9, our goal is to prove the following.
Theorem 13.
For the class of hypergraphs
![]() $G$
of maximum degree
$G$
of maximum degree
![]() $\Delta$
and maximum edge size
$\Delta$
and maximum edge size
![]() $k$
, and for complex
$k$
, and for complex
![]() $\lambda$
satisfying
$\lambda$
satisfying
![]() $| \lambda | \lt \lambda _s(\Delta +1)$
, there is an algorithm running in time
$| \lambda | \lt \lambda _s(\Delta +1)$
, there is an algorithm running in time
![]() $(n/\epsilon )^{O_{k,\Delta }(1)}$
that computes an
$(n/\epsilon )^{O_{k,\Delta }(1)}$
that computes an
![]() $\epsilon$
-relative approximation to
$\epsilon$
-relative approximation to
![]() $Z_G(\lambda )$
.
$Z_G(\lambda )$
.
Given a polynomial
![]() $Z(\lambda )$
with
$Z(\lambda )$
with
![]() $Z(0) =1$
, let
$Z(0) =1$
, let
![]() $T_r(\lambda )$
be the order-
$T_r(\lambda )$
be the order-
![]() $r$
truncation of the Taylor series for
$r$
truncation of the Taylor series for
![]() $\log Z(\lambda )$
around
$\log Z(\lambda )$
around
![]() $0$
. That is,
$0$
. That is,
 \begin{equation*} T_r(\lambda ) = \sum _{j=1}^r \frac {\lambda ^j}{j!} \frac {\partial ^j \log Z_G(\lambda ) }{\partial \lambda ^j} \,.\end{equation*}
\begin{equation*} T_r(\lambda ) = \sum _{j=1}^r \frac {\lambda ^j}{j!} \frac {\partial ^j \log Z_G(\lambda ) }{\partial \lambda ^j} \,.\end{equation*}
The connection between zero-freeness and approximation is provided by the following elementary but powerful lemma of Barvinok.
Lemma 14 (Barvinok [Reference Barvinok2]). Let
![]() $Z(\lambda )$
be a polynomial of degree at most
$Z(\lambda )$
be a polynomial of degree at most
![]() $N$
, and suppose that
$N$
, and suppose that
![]() $Z(\lambda ) \ne 0$
when
$Z(\lambda ) \ne 0$
when
![]() $|\lambda | \le B$
. Then for
$|\lambda | \le B$
. Then for
![]() $|\lambda |\lt B$
,
$|\lambda |\lt B$
,
We now prove Theorem 13.
Proof. Since
![]() $Z_G(\lambda )$
is a polynomial of degree at most
$Z_G(\lambda )$
is a polynomial of degree at most
![]() $n = |V(G)|$
, if
$n = |V(G)|$
, if
![]() $Z_G(\lambda )$
is zero-free in a disc of radius
$Z_G(\lambda )$
is zero-free in a disc of radius
![]() $B$
around
$B$
around
![]() $0$
and
$0$
and
![]() $|\lambda | \le (1-\delta )B$
then
$|\lambda | \le (1-\delta )B$
then
![]() $\exp (T_r(\lambda ))$
gives an
$\exp (T_r(\lambda ))$
gives an
![]() $\epsilon$
-relative approximation to
$\epsilon$
-relative approximation to
![]() $Z_G(\lambda )$
when
$Z_G(\lambda )$
when
![]() $r \ge C \log (n/\epsilon )$
, where
$r \ge C \log (n/\epsilon )$
, where
![]() $C$
is a constant that depends only on
$C$
is a constant that depends only on
![]() $\delta$
.
$\delta$
.
Thus to prove Theorem 13 given Theorem 1 we are left with the task of computing
![]() $T_r(\lambda )$
for
$T_r(\lambda )$
for
![]() $r = \Theta ( \log (n/\epsilon ))$
in time polynomial in
$r = \Theta ( \log (n/\epsilon ))$
in time polynomial in
![]() $n/\epsilon$
. Generalising the approach of Patel and Regts [Reference Patel and Regts47] to hypergraphs, Liu, Sinclair, and Srivastava [Reference Liu, Sinclair and Srivastava42] gave an algorithm to compute the first
$n/\epsilon$
. Generalising the approach of Patel and Regts [Reference Patel and Regts47] to hypergraphs, Liu, Sinclair, and Srivastava [Reference Liu, Sinclair and Srivastava42] gave an algorithm to compute the first
![]() $r$
coefficients of the partition function of a
$r$
coefficients of the partition function of a
![]() $2$
-spin model on a bounded-degree hypergraph. Since the coefficients of the Taylor series for
$2$
-spin model on a bounded-degree hypergraph. Since the coefficients of the Taylor series for
![]() $\log Z$
are related to the coefficients of
$\log Z$
are related to the coefficients of
![]() $Z$
through a triangular system of linear equations, this yields an algorithm to compute
$Z$
through a triangular system of linear equations, this yields an algorithm to compute
![]() $T_r(\lambda )$
. Specialising their result to the hypergraph independence polynomial yields the following, which finishes the proof of Theorem 13.
$T_r(\lambda )$
. Specialising their result to the hypergraph independence polynomial yields the following, which finishes the proof of Theorem 13.
Lemma 15 (Liu, Sinclair, Srivastava [Reference Liu, Sinclair and Srivastava42]). Fix
![]() $k$
,
$k$
,
![]() $\Delta$
, and
$\Delta$
, and
![]() $C\gt 0$
. Then there is an algorithm running in time polynomial in
$C\gt 0$
. Then there is an algorithm running in time polynomial in
![]() $n/\epsilon$
that computes
$n/\epsilon$
that computes
![]() $T_r(\lambda )$
for any hypergraph
$T_r(\lambda )$
for any hypergraph
![]() $G$
of maximum degree
$G$
of maximum degree
![]() $\Delta$
and maximum edge size
$\Delta$
and maximum edge size
![]() $k$
on
$k$
on
![]() $n$
vertices, where
$n$
vertices, where
![]() $r = \lceil C \log ( n/\epsilon ) \rceil$
.
$r = \lceil C \log ( n/\epsilon ) \rceil$
.

Figure 1. Obtaining
![]() $\Lambda/v$
from
$\Lambda/v$
from
![]() $\Lambda$
if
$\Lambda$
if
![]() $v$
is in a 2-edge.
$v$
is in a 2-edge.

Figure 2. Obtaining
![]() $\Lambda/v$
from
$\Lambda/v$
from
![]() $\Lambda$
if
$\Lambda$
if
![]() $v$
is not in a 2-edge.
$v$
is not in a 2-edge.

Figure 3. Obtaining
![]() $\Lambda/\{x_1,\dots,x_j\}$
from
$\Lambda/\{x_1,\dots,x_j\}$
from
![]() $\Lambda +\{x_1,\dots,x_j\}$
.
$\Lambda +\{x_1,\dots,x_j\}$
.
Acknowledgements
This work was done as part of an AIM SQuaRE workshop on ‘The Independence Polynomials of Hypergraphs’. We thank AIM and their staff for their support, and we thank Tyler Helmuth for very helpful preliminary conversations. We thank Wojciech Samotij for illuminating conversations and for providing the example in Proposition 2. We also thank Weiming Feng for carefully reading the manuscript and making valuable observations that improved the presentation of Theorem 10. DG is supported in part by the Simons Foundation. WP is supported in part by the NSF grant DMS-2309958. MS is supported in part by the Onassis Foundation – Scholarship F ZP 051-1/2019-2020. PT supported in part by the NSF grant DMS-2151283 and Alexander M. Knaster Professorship.