On the union of intersecting families

Abstract

A family of sets is said to be intersecting if any two sets in the family have non-empty intersection. In 1973, Erdős raised the problem of determining the maximum possible size of a union of r different intersecting families of k-element subsets of an n-element set, for each triple of integers (n, k, r). We make progress on this problem, proving that for any fixed integer r ⩾ 2 and for any $$k \le ({1 \over 2} - o(1))n$$, if X is an n-element set, and 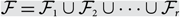$${\cal F} = {\cal F}_1 \cup {\cal F}_2 \cup \cdots \cup {\cal F}_r $$, where each 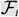$$ {\cal F}_i $$ is an intersecting family of k-element subsets of X, then $$|{\cal F}| \le \left( {\matrix{n \cr k \cr } } \right) - \left( {\matrix{{n - r} \cr k \cr } } \right)$$, with equality only if 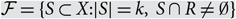$${\cal F} = \{ S \subset X:|S| = k,\;S \cap R \ne \emptyset \} $$ for some R ⊂ X with |R| = r. This is best possible up to the size of the o(1) term, and improves a 1987 result of Frankl and Füredi, who obtained the same conclusion under the stronger hypothesis 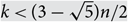$$k < (3 - \sqrt 5 )n/2$$, in the case r = 2. Our proof utilizes an isoperimetric, influence-based method recently developed by Keller and the authors.