Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T15:27:25.916Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Size-Ramsey Number of Cycles

Part of: Graph theory Extremal combinatorics

Published online by Cambridge University Press:  17 July 2019

R. Javadi ,
F. Khoeini ,
G. R. Omidi  and
A. Pokrovskiy
R. Javadi*
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan, 84156-83111, Iran. Emails: [email protected], [email protected], [email protected]
F. Khoeini
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan, 84156-83111, Iran. Emails: [email protected], [email protected], [email protected]
G. R. Omidi
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan, 84156-83111, Iran. Emails: [email protected], [email protected], [email protected] School of Mathematics, Institute for Research in Fundamental Sciences(IPM), PO box 19395-5746, Tehran, Iran
A. Pokrovskiy
Affiliation:
Department of Economics, Mathematics, and Statistics, Birkbeck, University of London, London WC1E 7HX, UK. Email: [email protected]
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

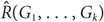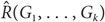For given graphs G1,…, Gk, the size-Ramsey number $\hat R({G_1}, \ldots ,{G_k})$ is the smallest integer m for which there exists a graph H on m edges such that in every k-edge colouring of H with colours 1,…,k, H contains a monochromatic copy of Gi of colour i for some 1 ≤ i ≤ k. We denote $\hat R({G_1}, \ldots ,{G_k})$ by 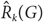${\hat R_k}(G)$ when G1 = ⋯ = Gk = G.

Haxell, Kohayakawa and Łuczak showed that the size-Ramsey number of a cycle Cn is linear in n, 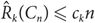${\hat R_k}({C_n}) \le {c_k}n$ for some constant ck. Their proof, however, is based on Szemerédi’s regularity lemma so no specific constant ck is known.

In this paper, we give various upper bounds for the size-Ramsey numbers of cycles. We provide an alternative proof of 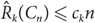${\hat R_k}({C_n}) \le {c_k}n$ , avoiding use of the regularity lemma, where ck is exponential and doubly exponential in k, when n is even and odd, respectively. In particular, we show that for sufficiently large n we have 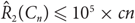${\hat R_2}({C_n}) \le {10^5} \times cn$ , where c = 6.5 if n is even and c = 1989 otherwise.

MSC classification

Primary: 05C55: Generalized Ramsey theory
Secondary: 05D10: Ramsey theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 28 , Issue 6 , November 2019 , pp. 871 - 880
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research partially supported by INSF grant no. 95844679.

‡

Research partially carried out in the IPM-Isfahan Branch and in part supported by a grant from IPM (no. 95050217).

§

Research partially supported by SNSF grant 200021-149111.

References

Alon, N. and Spencer, J. H. (2016) The Probabilistic Method, fourth edition, Wiley.Google Scholar
Balla, I., Pokrovskiy, A. and Sudakov, B. (2018) Ramsey goodness of bounded degree trees. Combin. Probab. Comput. 27 289–309.CrossRefGoogle Scholar
Beck, J. (1983) On size Ramsey number of paths, trees, and circuits I. J. Graph Theory 7 115–129.CrossRefGoogle Scholar
Bollobás, B. (2001) Random Graphs, Cambridge University Press.CrossRefGoogle Scholar
Conlon, D., Fox, J. and Sudakov, B. (2015) Recent developments in graph Ramsey theory. In Surveys in Combinatorics 2015, Cambridge University Press, pp. 49–118.CrossRefGoogle Scholar
Dudek, A. and Prałat, P. (2015) An alternative proof of the linearity of the size-Ramsey number of paths. Combin. Probab. Comput. 24 551–555.CrossRefGoogle Scholar
Dudek, A. and Prałat, P. (2017) On some multicolour Ramsey properties of random graphs. SIAM J. Discrete Math. 31 2079–2092.CrossRefGoogle Scholar
Erdős, P. (1947) Some remarks on the theory of graphs. Bull. Amer. Math. Soc. 53 292–294.CrossRefGoogle Scholar
Erdős, P., Faudree, R., Rousseau, C. and Schelp, R. (1978) The size Ramsey number. Period. Math. Hungar. 9 145–161.CrossRefGoogle Scholar
Erdős, P. and Szekeres, G.(1935) A combinatorial problem in geometry. Compositio Math. 2 463–470.Google Scholar
Faudree, R. and Schelp, R. (2002) A survey of results on the size Ramsey number. In Paul Erdös and his Mathematics, II (Budapest, 1999), Vol. 11 of Bolyai Society Mathematical Studies, Springer, pp. 291–309.Google Scholar
Haxell, P. E. and Kohayakawa, Y. (1995) The size-Ramsey number of trees. Israel J. Math. 89 261–274.CrossRefGoogle Scholar
Haxell, P. E., Kohayakawa, Y. and Łuczak, T. (1995) The induced size-Ramsey number of cycles. Combin. Probab. Comput. 4 217–239.CrossRefGoogle Scholar
Letzter, S. (2016) Path Ramsey number for random graphs. Combin. Probab. Comput. 25 612–622.CrossRefGoogle Scholar
Radziszowski, S. P. (1994) Small Ramsey numbers. Electron. J. Combin. 1 DS1.Google Scholar
Ramsey, F. P. (1930) On a problem of formal logic. Proc. London Math. Soc. 30 264–286.CrossRefGoogle Scholar