Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ilinca, L.
and
Kahn, J.
2012.
The number of 3-SAT functions.
Israel Journal of Mathematics,
Vol. 192,
Issue. 2,
p.
869.
Balogh, József
Dong, Dingding
Lidický, Bernard
Mani, Nitya
and
Zhao, Yufei
2023.
Nearly All 𝑘-SAT Functions Are Unate.
p.
958.


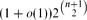 . One step in the proof determines the asymptotics of the number of ‘odd-blue-triangle-free’ graphs on
. One step in the proof determines the asymptotics of the number of ‘odd-blue-triangle-free’ graphs on 