No CrossRef data available.
Article contents
On the maximum number of edges in 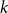 $k$-critical graphs
$k$-critical graphs
Published online by Cambridge University Press: 24 July 2023
Abstract
A graph is called 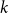 $k$-critical if its chromatic number is
$k$-critical if its chromatic number is 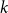 $k$ but every proper subgraph has chromatic number less than
$k$ but every proper subgraph has chromatic number less than 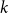 $k$. An old and important problem in graph theory asks to determine the maximum number of edges in an
$k$. An old and important problem in graph theory asks to determine the maximum number of edges in an  $n$-vertex
$n$-vertex 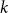 $k$-critical graph. This is widely open for every integer
$k$-critical graph. This is widely open for every integer 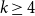 $k\geq 4$. Using a structural characterisation of Greenwell and Lovász and an extremal result of Simonovits, Stiebitz proved in 1987 that for
$k\geq 4$. Using a structural characterisation of Greenwell and Lovász and an extremal result of Simonovits, Stiebitz proved in 1987 that for 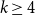 $k\geq 4$ and sufficiently large
$k\geq 4$ and sufficiently large  $n$, this maximum number is less than the number of edges in the
$n$, this maximum number is less than the number of edges in the  $n$-vertex balanced complete
$n$-vertex balanced complete 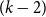 $(k-2)$-partite graph. In this paper, we obtain the first improvement in the above result in the past 35 years. Our proofs combine arguments from extremal graph theory as well as some structural analysis. A key lemma we use indicates a partial structure in dense
$(k-2)$-partite graph. In this paper, we obtain the first improvement in the above result in the past 35 years. Our proofs combine arguments from extremal graph theory as well as some structural analysis. A key lemma we use indicates a partial structure in dense 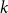 $k$-critical graphs, which may be of independent interest.
$k$-critical graphs, which may be of independent interest.
Keywords
MSC classification
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press



