On the edit distance function of the random graph

Abstract

Given a hereditary property of graphs 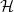$\mathcal{H}$ and a 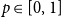$p\in [0,1]$ , the edit distance function 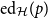$\textrm{ed}_{\mathcal{H}}(p)$ is asymptotically the maximum proportion of edge additions plus edge deletions applied to a graph of edge density p sufficient to ensure that the resulting graph satisfies 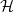$\mathcal{H}$ . 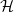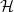The edit distance function is directly related to other well-studied quantities such as the speed function for $\mathcal{H}$ and the $\mathcal{H}$ -chromatic number of a random graph.

Let 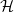$\mathcal{H}$ be the property of forbidding an Erdős–Rényi random graph 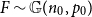$F\sim \mathbb{G}(n_0,p_0)$ , and let 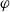$\varphi$ represent the golden ratio. In this paper, we show that if 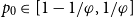$p_0\in [1-1/\varphi,1/\varphi]$ , then a.a.s. as 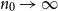$n_0\to\infty$ ,

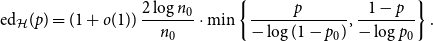\begin{align*} {\textrm{ed}}_{\mathcal{H}}(p) = (1+o(1))\,\frac{2\log n_0}{n_0} \cdot\min\left\{ \frac{p}{-\log(1-p_0)}, \frac{1-p}{-\log p_0} \right\}. \end{align*}

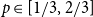Moreover, this holds for $p\in [1/3,2/3]$ for any 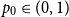$p_0\in (0,1)$ .

A primary tool in the proof is the categorization of p-core coloured regularity graphs in the range 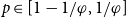$p\in[1-1/\varphi,1/\varphi]$ . Such coloured regularity graphs must have the property that the non-grey edges form vertex-disjoint cliques.