Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T01:59:37.326Z Has data issue: false hasContentIssue false
  • English
  • Français

On Ramsey numbers of hedgehogs

Part of: Graph theory

Published online by Cambridge University Press:  18 October 2019

Jacob Fox  and
Ray Li
Jacob Fox
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA 94305, USA
Ray Li*
Affiliation:
Department of Computer Science, Stanford University, Stanford, CA 94305, USA
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The hedgehog Ht is a 3-uniform hypergraph on vertices 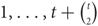$1, \ldots ,t + \left({\matrix{t \cr 2}}\right)$ such that, for any pair (i, j) with 1 ≤ i < j ≤ t, there exists a unique vertex k > t such that {i, j, k} is an edge. Conlon, Fox and Rödl proved that the two-colour Ramsey number of the hedgehog grows polynomially in the number of its vertices, while the four-colour Ramsey number grows exponentially in the square root of the number of vertices. They asked whether the two-colour Ramsey number of the hedgehog Ht is nearly linear in the number of its vertices. We answer this question affirmatively, proving that r(Ht) = O(t2 ln t).

MSC classification

Primary: 05C55: Generalized Ramsey theory
Secondary: 05C65: Hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 1 , January 2020 , pp. 101 - 112
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported by a Packard Fellowship, and by NSF Career Award DMS-1352121.

‡

Research supported by the National Science Foundation Graduate Research Fellowship Program under grant DGE-1656518.

References

Alon, N., Krivelevich, M. and Sudakov, B. (2003) Turán numbers of bipartite graphs and related Ramsey-type questions. Combin. Probab. Comput. 12 477–494.CrossRefGoogle Scholar
Burr, S. A. and Erdös, P. (1975) On the magnitude of generalized Ramsey numbers for graphs. In Infinite and Finite Sets, Vol. 1 (Keszthely, 1973), Vol. 10 of Colloq. Math. Soc. János Bolyai, pp. 214–240, North-Holland.Google Scholar
Conlon, D., Fox, J. and Rödl, V. (2017) Hedgehogs are not colour blind. J. Combin. 8 475–485.CrossRefGoogle Scholar
Conlon, D., Fox, J. and Sudakov, B. (2010) Hypergraph Ramsey numbers. J. Amer. Math. Soc. 23 247–266.CrossRefGoogle Scholar
Conlon, D., Fox, J. and Sudakov, B. (2015) Recent developments in graph Ramsey theory. In Survey in Combinatorics 2015, Vol. 424 of London Mathematical Society Lecture Note Series, pp. 49–118, Cambridge University Press.CrossRefGoogle Scholar
Erdös, P., Hajnal, A. and Rado, R. (1965) Partition relations for cardinal numbers. Acta Math. Acad. Sci. Hungar. 16 93–196.CrossRefGoogle Scholar
Erdös, P. and Rado, R. (1952) Combinatorial theorems on classifications of subsets of a given set. Proc. London Math. Soc. 3 417–439.CrossRefGoogle Scholar
Fox, J. and Sudakov, B. (2009) Two remarks on the Burr–Erdös conjecture. European J. Combin. 30 1630–1645.CrossRefGoogle Scholar
Graham, R. L., Rothschild, B. L. and Spencer, J. H. (1990) Ramsey Theory, second edition, Wiley.Google Scholar
Kostochka, A. V. and Rödl, V. (2006) On Ramsey numbers of uniform hypergraphs with given maximum degree. J. Combin. Theory Ser. A 113 1555–1564.CrossRefGoogle Scholar
Kostochka, A. V. and Sudakov, B. (2003) On Ramsey numbers of sparse graphs. Combin. Probab. Comput. 12 627–641.CrossRefGoogle Scholar
Lee, C. (2017) Ramsey numbers of degenerate graphs. Ann. of Math. 185 791–829.CrossRefGoogle Scholar