Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-12-03T19:27:20.658Z Has data issue: false hasContentIssue false
  • English
  • Français

On Partitioning and Packing Products with Rectangles

Published online by Cambridge University Press:  12 September 2008

Rudolf Ahlswede  and
Ning Cai
Rudolf Ahlswede
Affiliation:
Universität Bielefeld, Fakultät für Mathematik, Postfach 100131, 33501 Bielefeld, Germany
Ning Cai
Affiliation:
Universität Bielefeld, Fakultät für Mathematik, Postfach 100131, 33501 Bielefeld, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

In [1] we introduced and studied for product hypergraphs 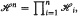where ℋi = (i,ℰi), the minimal size π(ℋn) of a partition of 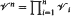into sets that are elements of . The main result was that

if the ℋis are graphs with all loops included. A key step in the proof concerns the special case of complete graphs. Here we show that (1) also holds when the ℋi are complete d-uniform hypergraphs with all loops included, subject to a condition on the sizes of the i. We also present an upper bound on packing numbers.

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 3 , Issue 4 , December 1994 , pp. 429 - 434
Copyright
Copyright © Cambridge University Press 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ahlswede, R. and Cai, N. (1993) On extremal set partitions in Cartesian product spaces. Combinatorics, Probability & Computing 2 211–220.CrossRefGoogle Scholar
[2]Ahlswede, R. and Cai, N. (1993) On poset partitions and hypergraph products, Preprint 93–008 of SFB 343, Diskrete Strukturen in der Mathematik, Bielefeld.Google Scholar
[3]Rota, G. C. (1964) On the foundations of combinatorial theory I. Möbius functions. Z. Wahrscheinlichkeitstheorie 2 340–368.CrossRefGoogle Scholar
[4]Stanley, R. P. (1986) Enumerative Combinatorics, Vol. i, Wadsworth & Brooks/Coll, Advanced Books & Software, Monterey, California.CrossRefGoogle Scholar