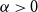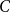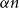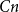On oriented cycles in randomly perturbed digraphs

Abstract

In 2003, Bohman, Frieze, and Martin initiated the study of randomly perturbed graphs and digraphs. For digraphs, they showed that for every $\alpha \gt 0$, there exists a constant $C$ such that for every $n$-vertex digraph of minimum semi-degree at least $\alpha n$, if one adds $Cn$ random edges then asymptotically almost surely the resulting digraph contains a consistently oriented Hamilton cycle. We generalize their result, showing that the hypothesis of this theorem actually asymptotically almost surely ensures the existence of every orientation of a cycle of every possible length, simultaneously. Moreover, we prove that we can relax the minimum semi-degree condition to a minimum total degree condition when considering orientations of a cycle that do not contain a large number of vertices of indegree $1$. Our proofs make use of a variant of an absorbing method of Montgomery.

1. Introduction

Hamilton cycles are one of the most studied objects in graph theory, and several classical results measure how ‘dense’ a graph needs to be to force a Hamilton cycle. In particular, in 1952 Dirac [9] proved that every $n$ -vertex graph with minimum degree $\delta (G) \geq n/2$ contains a Hamilton cycle; the minimum degree condition here is best possible.

The Hamiltonicity of directed graphs has also been extensively investigated since the 1960s. A directed graph, or digraph, is a set of vertices together with a set of ordered pairs of distinct vertices. We think of a digraph as a loop-free multigraph, where every edge is given an orientation from one endpoint to another, and there is at most one edge oriented in each of the two directions between a pair of vertices. An oriented graph is a digraph with at most one directed edge between every pair of vertices. An edge from vertex $u$ to vertex $v$ is represented as $\overrightarrow{uv}$ or $\overleftarrow{vu}$ . In the digraph setting, there is more than one natural analogue of the minimum degree of a graph. The minimum semi-degree $\delta ^0(D)$ of a digraph $D$ is the minimum of all the in- and outdegrees of the vertices in $D$ ; the minimum total degree $\delta (D)$ is the minimum number of edges incident to a vertex in $D$ . Ghouila-Houri [13] proved that every strongly connected $n$ -vertex digraph $D$ with minimum total degree $\delta (D)\geq n$ contains a consistently oriented Hamilton cycle, that is, a cycle $(v_1, v_2, \dots, v_n, v_{n+1}=v_1)$ with edges $\overrightarrow{v_i v_{i+1}}$ for all $i \in [n]$ . Note that there are $n$ -vertex digraphs $D$ with $\delta (D) = 3n/2 - 2$ that do not contain a consistently oriented Hamilton cycle, so the strongly connected condition in Ghouila-Houri’s theorem is necessary.

An immediate consequence of Ghouila-Houri’s theorem is that having minimum semi-degree $\delta ^0(D) \geq n/2$ forces a consistently oriented Hamilton cycle, and this is best possible. After earlier partial results [14, 15], DeBiasio, Kühn, Molla, Osthus, and Taylor [7] proved that this minimum semi-degree condition in fact forces all possible orientations of a Hamilton cycle, except for the anti-directed Hamilton cycle, that is, a cycle $(v_1, v_2, \dots, v_n, v_{n+1} = v_1)$ with edges $\overrightarrow{v_i v_{i+1}}$ for all odd $i \in [n]$ and $\overleftarrow{v_i v_{i+1}}$ for all even $i \in [n]$ , where $n$ is even. Earlier, DeBiasio and Molla [8] showed that the minimum semi-degree threshold for forcing the anti-directed Hamilton cycle is in fact $\delta ^0(D) \geq n/2+1$ .

There has also been interest in Hamilton cycles in random digraphs: the binomial random digraph $D(n,p)$ is the digraph with vertex set $[n]$ , where each of the $n(n-1)$ possible directed edges is present with probability $p$ , independently of all other edges. Recently, Montgomery [25] determined the sharp threshold for the appearance of any fixed orientation of a Hamilton cycle $H$ in $D(n,p)$ , thereby answering a conjecture of Ferber and Long [12] in a strong form. Depending on the orientation of $H$ , the threshold here can vary from $p=\log n/2n$ to $p=\log n/n$ .

In this paper, we find arbitrary orientations of Hamilton cycles in the randomly perturbed digraph model. Introduced in both the undirected and directed setting by Bohman, Frieze, and Martin [3], this model starts with a dense (di)graph and then adds $m$ random edges to it. The overarching question now is how many random edges are required to ensure that the resulting (di)graph asymptotically almost surely (a.a.s.) satisfies a given property, that is, with probability tending to $1$ as the number of vertices $n$ tends to infinity. For example, Bohman, Frieze, and Martin [3] proved that for every $\alpha \gt 0$ , there is a $C=C(\alpha )$ such that if we start with an arbitrary $n$ -vertex graph $G$ of minimum degree $\delta (G)\geq \alpha n$ and add $Cn$ random edges to it, then a.a.s. the resulting graph is Hamiltonian. Furthermore, given a constant $0\lt \alpha \lt 1/2$ , in a complete bipartite graph with part sizes $\alpha n$ and $(1-\alpha )n$ , a linear number of random edges are needed to ensure Hamiltonicity. Thus their result is best possible up to the dependence of $C$ on $\alpha$ . Subsequently, there has been a significant effort to improve our understanding of randomly perturbed graphs. See, e.g., [17, Section 1.3] and the references within for a snapshot of some of the results in the area.

Bohman, Frieze, and Martin [3] also proved the analogous result for consistently oriented Hamilton cycles in the randomly perturbed digraph model. Their result is also best possible up to the dependence of $C$ on $\alpha$ , for similar reasons as the undirected setting.

Theorem 1.1 (Bohman, Frieze, and Martin [3]). For every $\alpha \gt 0$ , there is a $C=C(\alpha )$ such that if $D_0$ is an $n$ -vertex digraph of minimum semi-degree $\delta ^0(D_0)\geq \alpha n$ , then $D_0 \cup D(n,C/n)$ a.a.s. contains a consistently oriented Hamilton cycle.

A notion closely related to Hamiltonicity is pancyclicity, which is when a (di)graph contains cycles of every possible length. Bondy [4] generalised Dirac’s theorem, showing that if $\delta (G) \geq n/2$ then $G$ is pancyclic or $K_{n/2,n/2}$ . Shortly after, Bondy [5] proposed his famous meta-conjecture that any ‘non-trivial’ sufficient condition for Hamiltonicity should be a sufficient condition for pancyclicity, up to a small number of exceptional graphs. Krivelevich, Kwan, and Sudakov [20] generalised Theorem 1.1 in this way, showing that the same conditions as in Theorem 1.1 imply that the randomly perturbed digraph contains consistently oriented cycles of every length.

Theorem 1.2 (Krivelevich, Kwan, and Sudakov [20]). For every $\alpha \gt 0$ , there is a $C=C(\alpha )$ such that if $D_0$ is an $n$ -vertex digraph of minimum semi-degree $\delta ^0(D_0)\geq \alpha n$ , then $D_0 \cup D(n,C/n)$ a.a.s. contains a consistently oriented cycle of every length between $2$ and $n$ .

The original rotation-extension-type proofs of Theorems 1.1 and 1.2 only guarantee consistently oriented cycles. Our main result is a generalisation of Theorem 1.2 to allow for all orientations of a cycle of every possible length. Moreover, we find all these cycles simultaneously, i.e., $D_0 \cup D(n,C/n)$ a.a.s. contains all of them. This last property is an example of universality, a notion both well-studied in the random graph (e.g., [10, 25]) and randomly perturbed (e.g., [6, 27]) settings.

Theorem 1.3. For every $\alpha \gt 0$ , there is a $C=C(\alpha )$ such that if $D_0$ is an $n$ -vertex digraph of minimum semi-degree $\delta ^0(D_0) \geq \alpha n$ , then $D_0 \cup D(n,C/n)$ a.a.s. contains every orientation of a cycle of every length between $2$ and $n$ .

Theorem 1.3 is best possible in the sense that one really needs to add a linear number of random edges to $D_0$ . Indeed, similarly as before, let $D$ be the complete bipartite digraph with part sizes $\alpha n$ and $(1-\alpha )n$ (where $0\lt \alpha \lt 1/2$ ). Then one needs to add a linear number of edges to $D$ to ensure a Hamilton cycle of any orientation.

It is also natural to try and generalise Theorem 1.1 in another direction, by relaxing the minimum semi-degree condition to a total degree. Unfortunately, this cannot be true for a Hamilton cycle $H$ in which all but $o(n)$ vertices have in- and outdegree $1$ . Indeed, given $0\lt \alpha \lt 1/2$ , let $D$ be the $n$ -vertex digraph which consists of vertex classes $S$ and $T$ of sizes $\alpha n$ and $(1-\alpha )n$ respectively, and whose edge set consists of all possible edges with their startpoint in $S$ and their endpoint in $T$ . Then whilst $\delta (D)= \alpha n$ , given any constant $C$ , with probability bounded away from $0$ , $D \cup D(n,C/n)$ contains a linear number of vertices with outdegree $0$ and a linear number of vertices with indegree $0$ , so it will not contain $H$ .

On the other hand, we show that this type of orientation of a Hamilton cycle is the only one we cannot guarantee. That is, our desired relaxation is possible for all orientations of a Hamilton cycle that contain a linear number of vertices of in- or outdegree $2$ .

Theorem 1.4. For every $\alpha, \eta \gt 0$ , there is a $C=C(\alpha, \eta )$ such that if $D_0$ is an $n$ -vertex digraph of minimum total degree $\delta (D_0) \geq 2\alpha n$ , then $D_0 \cup D(n,C/n)$ a.a.s. contains every orientation of a cycle of every length between $2$ and $n$ that contains at most $(1-\eta ) n$ vertices of indegree $1$ .

The proof of Theorem 1.4 has the same core ideas as the proof of Theorem 1.3, but there are additional complications and technicalities that come with the weakened degree condition.

Notation. Throughout this paper, we omit floors and ceilings whenever this does not affect the argument. Given a digraph $D$ we write $V(D)$ and $E(D)$ for its vertex and edge sets respectively. Given some $X \subseteq V(D),$ we write $D[X]$ for the induced subdigraph of $D$ with vertex set $X$ . Given some $x \in V(D)$ , $N_D^+(x)$ denotes the out-neighborhood of $x$ in $D$ , which is the set of vertices $y\in V(D)$ for which $\overrightarrow{xy} \in E(D)$ ; the outdegree of $x$ in $D$ is denoted by $d_D^+(x) \;:\!=\; |N_D^+(x)|$ . We define $N_D^-(x)$ and $d_D^-(x)$ analogously, and often omit the subscript when the digraph $D$ considered is clear from the context.

We write $\overleftrightarrow{u v}$ if $\overrightarrow{uv}$ and $\overleftarrow{uv}$ are edges and call $\overleftrightarrow{u v}$ a bidirected edge. A bidirected path is a digraph obtained from an undirected path by replacing each edge $uv$ with a bidirected edge $\overleftrightarrow{u v}$ . An oriented path is a digraph obtained from an undirected path by replacing each edge $uv$ with a single directed edge; either $\overrightarrow{uv}$ or $\overleftarrow{uv}$ . Given an oriented or bidirected path $P=(u_1,\dots,u_k)$ we call $u_1$ its startpoint and $u_k$ its endpoint, distinguishing it from the path $(u_k, \dots, u_1)$ .

Given an oriented path $P = (u_1, \dots, u_k)$ , we define $\sigma (u_i u_{i+1})$ to be $+$ if $\overrightarrow{u_i u_{i+1}} \in E(P)$ and $-$ otherwise. Given any $i\lt j$ , when clear from the context, we write $(u_i,\dots, u_j)$ to mean the oriented subpath of $P$ on vertices $u_i,\dots, u_j$ ; so crucially, the edges in $(u_i,\dots, u_j)$ are oriented precisely as in $P$ .

Given two oriented paths $P = (u_1, \dots, u_k)$ and $P' = (u'_{\!\!1}, \dots, u'_{\!\!k^{\prime}})$ with $u_k = u'_{\!\!1}$ and $V(P) \cap V(P') = \{u_k\}$ , the concatenation of $P$ and $P'$ , denoted $P \circ P'$ , is the path $(u_1, \dots, u_k, u'_{\!\!2}, u'_{\!\!3}, \dots, u'_{\!\!k^{\prime}})$ .

The paper is organised as follows. In the next section, we give an outline of the proof of Theorem 1.3. In Section 3 we collect together various properties of random and pseudorandom digraphs. The main work of the paper is the proof of our absorbing lemmas, one for each of our two theorems, which are given in Section 4 for Theorem 1.3 and Section 6 for Theorem 1.4. We prove Theorems 1.3 and 1.4 in Sections 5 and 7, respectively. In Section 8 we give some concluding remarks.

2. Overview of the proof of Theorem 1.3

Our goal is to show that for a given orientation $\mathcal{C}$ of a cycle, $D_0 \cup D(n,C/n)$ contains $\mathcal{C}$ with probability at least $1-e^{-n}$ . Theorem 1.3 follows from a union bound over all choices of $\mathcal{C}$ , of which there are trivially at most $n2^n$ . For the rest of this section, we consider only spanning $\mathcal{C}$ , as the non-spanning cycle case follows easily from the machinery we set up to deal with arbitrary orientations of a Hamilton cycle.

Let $D^*(n,p)$ denote the random digraph with vertex set $[n]$ where each possible pair of edges $\overrightarrow{uv}$ and $\overleftarrow{uv}$ are included together, independently of other edges, with probability $p$ . In this way $D^*(n,p)$ is the same as the binomial random graph $G(n,p)$ where we replace every undirected edge with a bidirected edge. Via a coupling argument from [22, 25], to prove that $D_0 \cup D(n,C/n)$ contains $\mathcal{C}$ with probability at least $1-e^{-n}$ , it suffices to show that $D_0 \cup D^*(n,C/n)$ contains $\mathcal{C}$ with probability at least $1-e^{-n}$ ; see Lemma 3.1 for the precise statement. This latter goal will be achievable as we only need to access the randomness in $D^*(n,C/n)$ through a simple pseudorandom property that is easily shown to hold with probability at least $1-e^{-n}$ ; see Definition 3.2.

Our argument applies the absorbing method, a technique that was introduced systematically by Rödl, Ruciński, and Szemerédi [28], but that has roots in earlier work (see, e.g., [19]).

2.1. A problem with absorbing

To highlight a key challenge we face with absorbing, we first describe a natural approach to absorbing in the case of a consistently oriented Hamilton cycle. We note though that absorbing was not the approach used in [3] to prove Theorem 1.1.

In this case, a ‘global absorber’ in $D_0 \cup D^*(n,C/n)$ is a structure $A$ on a small (but linear size) vertex set with the property that for every sufficiently small set of vertices $R$ , $A \cup R$ contains the consistently oriented path on $|V(A) \cup R|$ vertices with prescribed startpoint and endpoint in $R$ . If we can obtain such a structure $A$ , then we can proceed as follows: by applying the pseudorandom property of $ D^*(n,C/n)$ we find a bidirected path $Q$ in $ D^*(n,C/n)$ disjoint from $A$ that covers almost all of the vertices not in $A$ . Let $R$ be the set of vertices consisting of the startpoint $x$ and endpoint $y$ of $Q$ , together with all those vertices not in $Q$ or $A$ . Using the absorbing property of $A$ we ensure that there is a consistently oriented path $Q_R$ on $V(A) \cup R$ with startpoint $y$ and endpoint $x$ . Joining the startpoints and endpoints of $Q$ and $Q_R$ , we obtain a consistently oriented Hamilton cycle.

In this setting of consistently oriented Hamilton cycles, one can build the global absorber $A$ from a consistently oriented path $Q_A$ with the following property. Given any very small (but linear size) collection of vertices $R$ , we can find an ordering of the vertices $w_1,\dots,w_t$ in $R$ , and disjoint edges $\overrightarrow{x_iy_i}$ along $Q_A$ for each $i \in [t]$ where (i) if $i\lt j$ then $\overrightarrow{x_iy_i}$ comes before $\overrightarrow{x_jy_j}$ on $Q_A$ ; (ii) $\overrightarrow{x_iw_i}$ and $\overrightarrow{w_iy_i}$ are edges in $D_0$ for all $i \in [t]$ . In this case, we can ‘sandwich’ in $w_i$ between $x_i$ and $y_i$ on $Q_A$ , for all $i \in [t]$ , to obtain a consistently oriented path on $V(Q_A) \cup R$ . One can show such an oriented path $Q_A$ exists, and this forms the heart of the global absorbing set $A$ . ¹

For an arbitrary orientation of a Hamilton cycle $H$ , one may try to modify this argument. Indeed, fix some linear size oriented path $P_H$ which is a segment of $H$ . We would like to find an oriented path $Q_A$ in $D_0 \cup D^*(n,C/n)$ that has the property that after adding any very small arbitrary set $R$ of vertices to $V(Q_A)$ , there is a copy of $P_H$ precisely covering the vertices in $V(Q_A) \cup R$ .

To illustrate the difficulty for arbitrary orientations, choose two very small sets of vertices $R$ and $R'$ , both of which contain some fixed vertex $w$ . Suppose we have constructed a path $Q_A$ that does absorb both $R$ and $R'$ analogously to the consistently oriented case. Then depending on how we have ordered $R$ and $R'$ , $w$ might have to play the role of a different vertex along $P_H$ . More precisely, suppose $w$ is the $j$ th vertex in the ordering of $R$ and the $k$ th vertex in the ordering of $R'$ where $j\lt k$ . Then for $R'$ we will be sandwiching in more vertices before $w$ along $P_A$ than compared to $R$ . This means that the vertex in $P_H$ that $w$ plays the role of will be different in the $R$ and $R'$ cases. In particular, perhaps in the $R$ case, $w$ will need to play the role of a vertex in $P_H$ with outdegree $2$ , whilst in the $R'$ case, $w$ will need to play the role of a vertex with indegree $2$ . Furthermore, this cascading effect also means a vertex along $Q_A$ may have to play the role of a different vertex in $P_H$ depending on the choice of $R$ .

Of course, this would not be an issue if all the edges considered were bidirected. In that case, no matter where we sandwich in the vertices of $R$ or $R'$ in $Q_A$ , we have all the necessary edges to find a copy of $P_H$ , no matter how $P_H$ is oriented. Note that $D^*(n,C/n)$ by itself is too sparse to guarantee such a structure. For example, a.a.s. $D^*(n,C/n)$ does not contain a triangle containing a fixed vertex $w$ , and if we were to sandwich $w$ between two consecutive vertices $x_i$ and $y_i$ along $Q_A$ , then $x_i,y_i,w$ must form a triangle. Moreover, $D_0$ may not contain any bidirected edges at all. However, it turns out that we can guarantee that almost all the edges along $Q_A$ are from $D^*(n,C/n)$ and so are bidirected. The problem is that we will have to take the edges between $R$ and $Q_A$ to be deterministic, that is, from $D_0$ .

If there are many pairs of consecutive vertices $x_i,y_i$ along $Q_A$ which we can sandwich $w$ between, then this gives us some choice about how many other vertices we absorb before $w$ along the path $Q_A$ , potentially giving us the freedom to restrict which vertices of $P_H$ we require $w$ to play the role of. However, in our situation, $D_0$ may not be very dense, so in general it is not the case that there is a choice of $Q_A$ so that for every vertex $w$ outside of $Q_A$ , there are enough edges between $w$ and $Q_A$ in $D_0$ for this strategy to work.

As explained shortly, we will get around this problem by constructing $Q_A$ in a more sophisticated way so that ( $\alpha$ ) $Q_A$ is only used to absorb certain vertices, and ( $\beta$ ) $Q_A$ has some in-built structure so that if we absorb a vertex $w$ , it must always play the role of one of only a constant number of vertices along the path $P_H$ in $H$ , no matter what the set of vertices $R$ actually is. In particular, ( $\beta$ ) ensures that we do not need bidirected edges between $R$ and $Q_A$ ; rather, for a constant number of pairs of consecutive vertices $x_i,y_i$ along $Q_A$ , we need single edges of the correct orientation between $\{x_i,y_i\}$ and $w$ so we can sandwich $w$ in between the two.

2.2. Montgomery’s absorbing method

Montgomery [23, 24] introduced an approach to absorbing that has already found a number of applications, for example, to spanning trees in random graphs [23], decompositions of Steiner triple systems [11], and tilings in randomly perturbed graphs [17]. The basic idea of the method is to build a global absorber using a special graph $H_m$ as a framework. The bipartite graph $H_m$ has a bounded maximum degree with vertex classes $X \cup Y$ and $Z$ , and has the property that if one deletes any set of vertices of a given size from $X$ , then the resulting graph contains a perfect matching; see Lemma 4.6.

Roughly speaking, a global absorber is usually built from $H_m$ as follows: every edge $xy$ in $H_m$ is ‘replaced’ with a ‘local absorber’ $A_{xy}$ in such a way that all such absorbers $A_{xy}$ are vertex-disjoint. Here a local absorber $A_{xy}$ is some small gadget that can absorb a certain (constant size) set of vertices $S_{xy}$ .

A reason why this approach has found many applications is that, in some sense, it allows one to construct a global absorber in the case when one can only find ‘few’ local absorbers, where what is meant by ‘few’ here depends on the precise setting.

In the proofs of Theorems 1.3 and 1.4, we will use $H_m$ again as a framework to build a global absorber. The reason we use $H_m$ , however, is different from most applications of the method (although morally the reason is similar to why Montgomery used this method in [23]). In particular, the key idea is that one can use this framework as a way of guaranteeing property ( $\beta$ ) above. More precisely, in our case, we will replace every edge in $H_m$ incident to $z \in Z$ with the same local absorbing gadget $A_z$ . Here $A_z$ is not designed to absorb a fixed set of vertices like before; rather, it has some local flexibility about what vertices it will absorb; see Definition 4.2. The idea is that constructing the global absorber in this way gives us the flexibility to know in advance precisely which (constant size) set of vertices on $P_H$ an absorbed vertex $w$ can play the role of.

We emphasise that this version of Montgomery’s method should be useful when trying to apply absorption to embed any spanning structure in a digraph that does not have some ‘nice’ orientation.

3. Random digraph ingredients

Recall that $D(n,p)$ is the digraph with vertex set $[n]$ where each of the $n(n-1)$ possible directed edges is present with probability $p$ , independently of all other edges; $D^*(n,p)$ is the digraph with vertex set $[n]$ where each possible pair of edges $\overrightarrow{uv}$ and $\overleftarrow{uv}$ are included together, independently of other edges, with probability $p$ .

We will use the following result, observed by Montgomery [25, Theorem 3.1] as a consequence of McDiarmid’s coupling argument [22]. Recall that an oriented graph is a digraph in which there is at most one edge between any pair of vertices.

Lemma 3.1 ([22, 25]). Let $p \in [0, 1]$ and $n \in \mathbb{N}$ . Let $\mathcal{H}$ be a set of oriented graphs with vertex set $[n]$ and let $D_0$ be a digraph with vertex set $[n]$ . Then

\begin{equation*}\mathbb {P}(\exists H \in \mathcal {H}\;:\; H \subset D_0 \cup D(n,p)) \ge \mathbb {P}(\exists H \in \mathcal {H}\;:\; H \subset D_0 \cup D^*(n,p))\,.\end{equation*}

Note the direction of the inequality in the conclusion of Lemma 3.1. The obvious coupling between these two models gives

\begin{equation*} \mathbb {P}(\exists H \in \mathcal {H} \;:\; H \subseteq D_0 \cup D(n,p)) \leq \mathbb {P}(\exists H \in \mathcal {H} \;:\; H \subseteq D_0 \cup D^*(n,2p-p^2)),\end{equation*}

where the inequality is in the opposite direction but the edge-probabilities for the two models are different.

For our purposes, $\mathcal{H}$ will consist of all possible copies of a single specific orientation of a cycle $\mathcal{C}$ . Lemma 3.1 says that it is at least as difficult to find $\mathcal{C}$ in $D_0 \cup D^*(n,p)$ as it is in $D_0 \cup D(n,p)$ . By showing that $D_0 \cup D^*(n,p)$ contains $\mathcal{C}$ with probability at least $1-e^{-n}$ , we can use a union bound to show that a.a.s. $D_0 \cup D(n,p)$ contains all our desired orientations of a cycle of every length.

As is often the case with random (di)graph arguments, we only access the randomness through a particular sparse pseudorandom property.

Definition 3.2 (Pseudorandom). For $1\le t \le n/2$ , an $n$ -vertex digraph $D$ is $t$ -pseudorandom if for every $U,W \subseteq V(D)$ with $|U|=|W|=t$ and $U \cap W = \emptyset$ , there is an edge $\overrightarrow{uw}$ directed from $U$ to $W$ . Moreover, if $D$ contains both $\overrightarrow{uw}$ and $\overleftarrow{uw}$ for every such $U$ and $W$ , then we call it $t$ -bipseudorandom.

Ben-Eliezer, Krivelevich, and Sudakov [2, Claim 4.3 and Lemma 4.4] proved versions of the following two lemmas for $t$ -pseudorandom digraphs. The proofs for the $t$ -bipseudorandom versions are identical, so we omit them.

Lemma 3.3 (Connecting Lemma). Suppose that $D$ is a $t$ -bipseudorandom digraph and $B_1, \dots, B_\ell \subseteq V(D)$ are pairwise disjoint sets with $|B_i| \geq 2t$ for every $i \in [\ell ]$ . Then there is a bidirected path $(v_1, \dots, v_\ell )$ in $D$ with $v_i \in B_i$ for every $i \in [\ell ]$ .

Lemma 3.4. If $D$ is an $n$ -vertex $t$ -bipseudorandom digraph, then $D$ has a bidirected path on at least $n-2t$ vertices.

In order to use the previous lemmas, we observe that $D^*(n,C/n)$ is $\varepsilon n$ -bipseudorandom with very high probability. We typically assume that $\varepsilon n$ is an integer and ignore inconsequential rounding.

Lemma 3.5. Let $0\lt \varepsilon \lt 1/2$ and let $C \geq \frac{4}{\varepsilon } \log \frac{e}{\varepsilon }$ . Then, with probability at least $1-\exp\!(-C\varepsilon ^2 n/2)$ , the random digraph $D^*(n,C/n)$ is $\varepsilon n$ -bipseudorandom.

Proof. Let $B_1$ and $B_2$ be disjoint subsets of vertices of size $\varepsilon n$ . In $D^*(n,C/n)$ , the probability that there is no edge between $B_1$ and $B_2$ is $(1-C/n)^{(\varepsilon n)^2}$ . Taking a union bound over all possible sets $B_1$ and $B_2$ of size exactly $\varepsilon n$ , we get that the probability that there is some disjoint $B_1$ and $B_2$ with no edge between $B_1$ and $B_2$ is at most

\begin{equation*} \binom {n}{\varepsilon n}^2 \left (1-\frac {C}{n}\right )^{(\varepsilon n)^2} \leq \exp\!\left ( 2 \varepsilon n \log \frac {e}{\varepsilon } - C \varepsilon ^2 n \right ) \leq \exp\! \left ( - \frac {C \varepsilon ^2 n}{2} \right ) .\end{equation*}

4. The semi-degree absorbing lemma

Following the framework sketched in Section 2, in this section, we define and construct our global and local absorbers, Definitions 4.1 and 4.2, respectively. Moreover, we prove the existence of many local absorbers which will then be used to construct a global absorber. For the latter, we use Montgomery’s technique [23, 24] based on the existence of a sparse auxiliary bipartite graph $H_m$ with ‘robust’ matching properties; see Lemma 4.6.

In this section, we do not work in the random model; instead, our results are stated for $\varepsilon n$ -bipseudorandom digraphs with minimum semi-degree at least $\alpha n$ . In Section 5, we apply the main absorbing lemma, Lemma 4.7, to the randomly perturbed model to prove Theorem 1.3.

Definition 4.1 (Global absorber). Let $P$ be an oriented path and let $D$ be a digraph. A subset $A \subseteq V(D)$ is called a $P$ -global absorber if for every $R \subseteq V(D) \setminus A$ such that $\vert R\vert + \vert A\vert = \vert V(P)\vert$ , and for every pair of distinct vertices $v,v'\in R$ , there is a copy of $P$ in $D[A\cup R]$ with startpoint $v$ and endpoint $v'$ .

Definition 4.2 (Local absorber). Let $P$ be an oriented path, $D$ be a digraph, $S\subseteq V(D)$ , and $z\in V(D)\setminus S$ . A pair $(A,v)$ is a $P$ -absorber for $(S,z)$ if

• $A \subseteq V(D) \setminus (S \cup \{z\})$ is a set of $|V(P)|-2$ vertices,

• $v \in A$ ,

• for every $s \in S$ , $D[A \cup \{s,z\}]$ contains a copy of $P$ with startpoint $v$ and endpoint $z$ .

We call $v$ the startpoint of the $P$ -absorber $(A,v)$ .

The next lemma guarantees the existence of local absorbers with prescribed startpoint avoiding any small set of vertices – this ensures that all the local absorbers we find will be vertex-disjoint. Before this, we prove a simple consequence of the pseudorandom property that will be useful later. Recall that for an oriented path $P = (u_1, \dots, u_k)$ , $\sigma (u_i u_{i+1}) = +$ if $\overrightarrow{u_i u_{i+1}} \in E(P)$ and $\sigma (u_i u_{i+1}) =-$ otherwise.

Proposition 4.3. Let $n, t \in \mathbb N$ where $1\leq t \lt n/2$ . Suppose that $D$ is an $n$ -vertex $t$ -bipseudorandom digraph with $\delta ^0(D)\geq 2t + 1$ . For every oriented path $P$ on $3$ edges and every distinct $v, v' \in V(D)$ , there is a copy of $P$ in $D$ with startpoint $v$ and endpoint $v'$ .

Proof. Let $P = (u_1, u_2, u_3, u_4)$ . Let $B_1 \;:\!=\; N^*(v)$ for $* = \sigma (u_1 u_2)$ , and let $B_2 \;:\!=\; N^*(v')$ for $* = \sigma (u_4 u_3)$ . Since $|B_1|, |B_2| \geq 2t + 1$ , there exists disjoint subsets $B'_{\!\!1} \subseteq B_1$ and $B'_{\!\!2} \subseteq B_2$ with $|B'_{\!\!1}|, |B'_{\!\!2}| \ge t$ which do not contain $v$ or $v'$ . Since $D$ is $t$ -bipseudorandom, there exists a bidirected edge $\overleftrightarrow{v_1 v_2}$ in $D$ with $v_1 \in B'_{\!\!1}$ and $v_2 \in B'_{\!\!2}$ . Then $(v, v_1, v_2, v')$ contains a copy of $P$ with startpoint $v$ and endpoint $v'$ .

Lemma 4.4. Let $n,k\in \mathbb N$ and $\alpha, \varepsilon \gt 0$ , so that $\alpha n \geq 4k+4$ and $\alpha \geq 8 (2k+2)\varepsilon$ . Let $D$ be an $n$ -vertex $\varepsilon n$ -bipseudorandom digraph with $\delta ^0(D) \geq \alpha n$ . Let $U \subseteq V(D)$ so that $|U| \leq \alpha n/2$ , and let $v \in V(D) \setminus U$ . For every oriented path $P$ on $2k+5$ vertices, every vertex set $S\subseteq V(D)\setminus \{v\}$ of size $k$ , and every vertex $z\in V(D) \setminus (S\cup \{v\})$ , there exists a $P$ -absorber $(A,v)$ for $(S, z)$ disjoint from $U$ .

Proof. Fix $P=(u_1, \dots, u_{2k+5})$ and an ordering $s_1, \dots, s_{k}$ of $S$ . We will find a $P$ -absorber for $(S,z)$ by applying Lemma 3.3 to various neighbourhoods of the $s_i$ , $v$ and $z$ . For each $i \in [k]$ , define

• $B_1 \;:\!=\; N^*(v)$ , where $* = \sigma (u_1 u_2)$ ,

• $B_{2i} \;:\!=\; N^*(s_i)$ , where $* = \sigma (u_{2i+2} u_{2i+1})$ ,

• $B_{2i+1} \;:\!=\; N^*(s_i)$ , where $* = \sigma (u_{2i+2} u_{2i+3})$ ,

• $B_{2k+2} \;:\!=\; N^*(z)$ , where $* = \sigma (u_{2k+5} u_{2k+4})$ .

Because of the minimum degree condition, $\vert B_i\vert \geq \alpha n$ , and therefore, we may take pairwise disjoint subsets $B'_{\!\!i}\subseteq B_i\setminus (U\cup S \cup \{z\})$ such that

\begin{equation*}\vert B'_{\!\!i}\vert \geq \frac {(\alpha n -\tfrac {\alpha }{2}n-k-1)}{2k+2} \geq \frac {\alpha n}{4(2k+2)} \geq 2\varepsilon n.\end{equation*}

Hence, an application of Lemma 3.3 yields a bidirected path $(v_1,\dots, v_{2k+2})$ such that $v_i\in B'_{\!\!i}$ for every $i\in [2k+2]$ .

Let $A \;:\!=\; \{v, v_1, \dots, v_{2k+2}\}$ . To see that $(A,v)$ is a $P$ -absorber for $(S,z)$ , observe that for every $s_i\in S$ , the pairs $(u_{2i+1},u_{2i+2})$ and $(u_{2i+2},u_{2i+3})$ in $P$ have the same directions of the underlying edges as the edges from the pairs $(v_{2i},s_i)$ and $(s_i,v_{2i+1})$ , allowing $s_i$ to play the role of $u_{2i+2}$ in $P$ ; see Figure 1. More precisely,

\begin{equation*} (v, v_1, \dots, v_{2i}, s_i, v_{2i+1}, \dots, v_{2k+2}, z) \end{equation*}

is a copy of $P$ in $D[A \cup \{s_i, z\}]$ with startpoint $v$ and endpoint $z$ .

Figure 1. An example of a $P$ -absorber $(A,v)$ for $(S,z)$ from Lemma 4.4 with $k=|S|=3$ . The double edges indicate that both orientations are present. For every $i\in \{1,2,3\}$ , $A \cup \{s_i, z\}$ contains a copy of $P$ in which vertex $v$ plays the role of $u_1$ , vertex $z$ plays the role of $u_{11}$ , vertex $s_i$ plays the role of $u_{2i+2}$ , and $v_j$ plays the role of $u_{j+1}$ for $j \leq 2i$ and $u_{j+2}$ for $j\gt 2i$ .

Our global absorber works in the following two-step approach: given a set $R$ of vertices we wish to absorb, we first absorb $R$ using some vertices from a specific vertex set $X$ within our global absorber; then the rest of the global absorber essentially absorbs what is left of $X$ in order to create a copy of the desired oriented path $P$ . The following lemma will be used to undertake the first step of this approach; it follows easily from Lemma 3.4 and Proposition 4.3.

Lemma 4.5. Let $5/n \lt \varepsilon \lt \beta \lt 1$ , and let $m$ and $\beta m$ be integers such that $\beta m \geq 5\varepsilon n$ . Let $D$ be an $n$ -vertex $\varepsilon n$ -bipseudorandom digraph, and suppose there is a set $X\subseteq V(D)$ of size $(1+\beta )m$ such that for every $v\in V(D)$ and for every $* \in \{+,-\}$ , $\vert N^*(v)\cap X\vert \geq 2\beta m$ . Let $R\subseteq V(D)\setminus X$ be such that $|R|\geq 2$ , and let $v,v' \in R$ be distinct. Then, for every oriented path $P$ on $|R| +\beta m$ vertices, there exists a copy of $P$ in $D[R\cup X]$ with startpoint $v$ and endpoint $v'$ that covers $R$ .

Proof. Let $X$ , $R$ , $v$ , and $v'$ be as in the statement of the lemma. Fix an arbitrary orientation of a path $P = (u_1, \dots, u_k)$ on $k \;:\!=\; |R| +\beta m$ vertices. Let $t \;:\!=\; 2\varepsilon n$ , and $X'\subseteq X$ be an arbitrary set of size $\beta m - 2t - 4 \geq \varepsilon n - 4 \gt 0$ . Let $R_0\;:\!=\;R\cup X'\setminus \{v,v'\}$ and $X_0\;:\!=\;X\setminus X'$ .

Observe that $D[R_0]$ is $\varepsilon n$ -bipseudorandom, so an application of Lemma 3.4 yields a bidirected path $Q_{\leftrightarrow }$ on exactly

(4.1) \begin{equation} |R_0| - 2 \varepsilon n = |R| -2 + |X'| - t = |R| +\beta m - 3t -6 \end{equation}

vertices. Denote by $w$ and $w'$ the startpoint and endpoint of $Q_\leftrightarrow$ , respectively.

Label $(R_0 \setminus V(Q_\leftrightarrow )) \cup \{v,w\}$ as $\{v_0 = v, v_1, \dots, v_t, v_{t+1}=w\}$ . For each $0 \leq i \leq t$ , we find a copy $(v_i, x_i, x'_{\!\!i}, v_{i+1})$ of the subpath $(u_{3i+1}, u_{3i+2}, u_{3i+3}, u_{3i+4})$ of $P$ , and we also find a copy $(w', x, x', v')$ of the subpath $(u_{k-3}, u_{k-2}, u_{k-1}, u_k)$ of $P$ , with $x_i, x'_{\!\!i}, x, x' \in X_0$ all distinct. This is possible by applying Proposition 4.3, observing that in total we will use $2(t+2)$ vertices of $X_0$ , and for any $U \subseteq X_0$ with $|U| \leq 2(t+2)$ and any $z, z' \in V(D) \setminus X_0$ , we have

\begin{equation*} \delta ^0(D[(X_0 \setminus U) \cup \{z,z'\}]) \geq 2\beta m - |X'| - |U| \geq \beta m \geq 2\varepsilon n + 1 .\end{equation*}

Recall that $\circ$ denotes concatenation. Thus $(v_0, x_0, x'_{\!\!0}, v_1, x_1, x'_{\!\!1}, v_2, \dots, v_{t+1}) \circ Q_\leftrightarrow \circ (w', x, x', v')$ contains a copy of $P$ with startpoint $v$ and endpoint $v'$ , since $3t+3 + |V(Q_\leftrightarrow )| + 3 = |R| + \beta m = k$ by (4.1); see Figure 2.

The next lemma provides the sparse auxiliary bipartite graph $H_m$ with robust matching properties that we use as a framework to build our global absorber.

Lemma 4.6 ([24]). For every $0\lt \beta \leq 1$ and for sufficiently large $m \in \mathbb{N}$ with $\beta m \in \mathbb{N}$ , there exists a bipartite graph $H_m$ with parts $X \dot \cup Y$ and $Z$ , such that $|X|=(1+\beta )m$ , $|Y| = 2m$ , $|Z| = 3m$ , $H_m$ has maximum degree at most $40$ , and for every $X' \subseteq X$ of size $m$ , there exists a perfect matching between $X' \cup Y$ and $Z$ in $H_m$ .

We are now ready to prove the absorbing lemma for Theorem 1.3.

Lemma 4.7 (Absorbing lemma). For every $0 \lt \alpha, \eta \leq 1$ , there exists an $0\lt \varepsilon \lt \alpha \eta/1000$ such that the following holds for sufficiently large $n$ . Given an oriented path $P$ of size $\lceil \alpha n/4\rceil$ , every $\varepsilon n$ -bipseudorandom $n$ -vertex digraph $D$ with $\delta ^0(D) \geq \alpha n$ contains a $P$ -global absorber $A$ of size at most $\eta |V(P)|$ .

Proof. Given $\alpha$ and $\eta$ , define $p \;:\!=\;{\eta \alpha }/{2024}$ . Set $\beta \;:\!=\;\alpha/10$ and $\varepsilon \;:\!=\; p \beta/{6}$ . Let $P=(u_1, \dots, u_k)$ with $k\;:\!=\;\lceil \alpha n/4\rceil$ .

By applying the Chernoff bound for the hypergeometric distribution, we obtain a set $X \subseteq V(D)$ such that

1. (X1) $|X| = (1+\beta )m$ with $p n \lt m \lt |X| \lt 2p n$ and $\beta m \geq 5\varepsilon n +2$ , where we assume that $m$ and $\beta m$ are integers and ignore inconsequential rounding issues;

2. (X2) for every vertex $v \in V(D)$ and for every $* \in \{+,-\}$ , $|N^*(v) \cap X| \geq \frac{p}{2}|N^*(v)|\geq \frac{p\alpha n}{2} \geq 2\beta m +2$ .

Note that $X$ satisfies the hypothesis of Lemma 4.5, which will be used later. Arbitrarily choose two disjoint sets $Y, Z\subseteq V(D)\setminus X$ of sizes $2m$ and $3m$ , respectively. We form an auxiliary graph $H_m$ isomorphic to the graph from Lemma 4.6 on $X \cup Y \cup Z$ . We label $Z$ as $\{z_1, \dots, z_{3m}\}$ , and let $N_i \subseteq X \cup Y$ be a set of size exactly $40$ containing $N_{H_m}(z_i)$ .

We are now ready to construct the global absorber. We will identify a particular segment of $P$ for each $i \in [3m]$ , and use Lemma 4.4 to obtain a local absorber for $(N_i,z_i)$ for such a segment. These local absorbers combined will act as a global absorber since we can apply Lemma 4.5 to form the rest of $P$ with any appropriate set $R$ of vertices we wish to absorb, using exactly $\beta m$ vertices of $X$ in the process; the remaining part of $X$ along with $Y$ is matched to $Z$ via the property of $H_m$ given in Lemma 4.6, and this matching will tell us how to use each local absorber; see Figure 3.

Figure 2. A copy of $P$ in $D[R\cup X]$ with startpoint $v$ and endpoint $v'$ that covers all the vertices in $R$ , as found in Lemma 4.5.

Figure 3. The global absorber. The blue path with startpoint $v$ and endpoint $v'$ is a copy of $P$ covering $R$ , $X$ , $Y$ , and $Z$ . The red edges are the matching in the auxiliary graph $H_m$ , dictating which local absorber $A_i$ to use for each vertex in $X \cup Y$ .

Let $z_0 \in V(D) \setminus (X \cup Y \cup Z)$ be arbitrary. For each $i \in [3m]$ , we find a $(u_{84i-80}, \dots, u_{84i+4})$ -absorber $(A_i,z_{i-1})$ for $(N_i, z_i)$ such that $z_{i-1} \in A_i$ , the sets $A_i$ for $i\in [3m]$ are pairwise disjoint and disjoint from $X \cup Y \cup \{z_{3m}\}$ . ² This is possible by applying Lemma 4.4 (with $40$ playing the role of $k$ ) since we require the absorbers to be disjoint from at most

(4.2) \begin{equation} |A| = |X \cup Y| + 1 + \sum _{i=1}^{3m} |A_i| = 1 + (3+\beta )m + 3m\cdot 83 = (252+\beta )m+1 \leq \eta |V(P)| \leq \alpha n/2 \end{equation}

vertices, where we define

\begin{equation*} A \;:\!=\; X \cup Y \cup \{z_{3m}\} \cup \bigcup _{i \in [3m]} A_i .\end{equation*}

We claim that $A$ is a $P$ -global absorber, which by (4.2) has size at most $\eta |V(P)|$ .

Let $R \subseteq V(D) \setminus A$ be such that $|R| + |A| = |V(P)| = k$ , and let $v,v' \in R$ be distinct. By (X1) and (X2), we have that $\delta ^0(D[X \cup \{v, z_0\}]) \geq 2\beta m \geq 10\varepsilon n \geq 2 \varepsilon n +1$ , so we may apply Proposition 4.3 to obtain a copy $(v, x_1, x_2, z_0)$ of $(u_1, u_2, u_3, u_4)$ , where $x_1, x_2 \in X$ .

Let $\bar{X} \;:\!=\; X \setminus \{x_1, x_2\}$ , let $\bar{\beta } \;:\!=\; \beta - \frac{2}{m}$ , and let $\bar{R} \;:\!=\; (R \cup \{z_{3m}\}) \setminus \{v\}$ . By (X1), $|\bar{X}| = (1+\bar{\beta })m \geq m + 5\varepsilon n$ , and by (X2), for every $v \in V(D)$ and for every $* \in \{+,-\}$ , we have $|N^*(v) \cap \bar{X}| \geq 2\beta m$ . Therefore we may apply Lemma 4.5 to obtain a copy $Q$ of $(u_{252m+4}, \dots, u_k)$ in $D[\bar{X} \cup \bar{R}]$ covering $\bar{R}$ and exactly $\bar{\beta } m$ vertices of $\bar{X}$ with startpoint $z_{3m}$ and endpoint $v'$ .

Now we activate the local absorbers. Let $X' \;:\!=\; \bar{X} \setminus V(Q)$ , and note that $|X'| = m$ . By Lemma 4.6, there exists a matching between $Z$ and $X' \cup Y$ in $H_m$ . Fixing such a matching, let $z'_{\!\!i} \in N_i$ be the vertex matched to $z_i$ for each $i \in [3m]$ . Since $(A_i, z_{i-1})$ is a $(u_{84i-80}, \dots, u_{84i+4})$ -absorber for $(N_i, z_i)$ , there exists a copy $Q_i$ of $(u_{84i-80}, \dots, u_{84i+4})$ in $D[A_i \cup \{z_i, z'_{\!\!i}\}]$ with startpoint $z_{i-1}$ and endpoint $z_i$ . Concatenating as

\begin{equation*} (v, x_1, x_2, z_0) \circ Q_1 \circ \cdots \circ Q_{3m} \circ Q,\end{equation*}

we obtain a copy of $P$ in $D[A \cup R]$ with startpoint $v$ and endpoint $v'$ .

5. Proof of Theorem 1.3

Proof of Theorem 1.3. Given $\alpha \gt 0$ , let $\varepsilon \gt 0$ be as in Lemma 4.7 on input $\alpha$ and $\eta \;:\!=\; 1/2$ . Set $C \;:\!=\; 4e/\varepsilon ^2$ . Let $D_0$ be an $n$ -vertex digraph with $\delta ^0(D_0)\geq \alpha n$ .

Given any orientation of a cycle $\mathcal C$ of length between $3$ and $n$ , our first aim is to prove that $D\;:\!=\;D_0\cup D^*(n, C/n)$ contains a copy of $\mathcal C$ with probability at least $1-e^{-n}$ . Note that Lemma 3.5 implies that $D^*(n, C/n)$ is $\varepsilon n$ -bipseudorandom with probability at least $1-e^{-n}$ ; thus, we may assume that $D$ is $\varepsilon n$ -bipseudorandom.

If $|\mathcal C| = 3$ , we use a proof similar to that of Proposition 4.3. Fix a vertex $v \in V(D)$ , and consider $N^+_D(v)$ and $N^-_D(v)$ , which both have size at least $\alpha n \geq 2\varepsilon n$ . Between these sets there is a bidirected edge, giving both possible orientations of $\mathcal C$ .

If $4 \leq \vert \mathcal C\vert \leq \alpha n/2$ , then we apply Lemma 3.4 to find a bidirected path $Q_\leftrightarrow$ in $D$ on $\vert \mathcal C\vert - 2$ vertices. Let $v$ and $v'$ be the startpoint and endpoint of $Q_\leftrightarrow$ , respectively, and let $P$ be a subpath of $\mathcal C$ on $3$ edges. Observe that $\delta ^0(D[(V(D)\setminus V(Q_\leftrightarrow )) \cup \{v,v'\}])\geq \alpha n/2 \geq 2\varepsilon n+1$ , and hence we may apply Proposition 4.3 to find a copy $Q$ of $P$ in $D$ with startpoint $v'$ and endpoint $v$ . Joining $Q$ and $Q_\leftrightarrow$ at both ends, we obtain a copy of $\mathcal C$ in $D$ .

If $|\mathcal C| \geq \alpha n/2$ , then let $P$ be a subpath of $\mathcal{C}$ on $\lceil{\alpha n/4}\rceil$ vertices. We apply Lemma 4.7 to find a $P$ -global absorber $A$ of size at most $\lceil{\alpha n/8}\rceil$ . Since $D[V(D)\setminus A]$ is $\varepsilon n$ -bipseudorandom, Lemma 3.4 yields a bidirected path on at least $n - |A| - 2\varepsilon n \gt n-|P|+2$ vertices disjoint from $A$ . Ignoring some vertices, let $Q_\leftrightarrow$ be a bidirected path on $\vert \mathcal C\vert -|P|+2$ vertices in $D[V(D) \setminus A]$ , and let $v$ and $v'$ be the startpoint and endpoint of $Q_\leftrightarrow$ , respectively. Let $R \subseteq (V(D) \setminus (V(Q_\leftrightarrow ) \cup A)) \cup \{v, v'\}$ with $v,v' \in R$ and $|R| = |P| - |A|$ . By Definition 4.1, there is a copy $Q$ of $P$ in $D$ with startpoint $v'$ and endpoint $v$ covering exactly the vertices of $R\cup A$ . Joining $Q$ and $Q_\leftrightarrow$ at both ends, we obtain a copy of $\mathcal C$ in $D$ .

Thus, for every orientation of a cycle $\mathcal C$ of length between $3$ and $n$ we have that $D_0 \cup D^*(n,C/n)$ contains a copy of $\mathcal C$ with probability at least $1-e^{-n}$ . By Lemma 3.1, $D_0 \cup D(n,C/n)$ contains a copy of $\mathcal C$ with probability at least $1-e^{-n}$ . Taking a union bound over all $n-2$ possible lengths and all at most $2^n$ possible orientations of each length, we have that $D_0 \cup D(n,C/n)$ contains every orientation of a cycle of length between $3$ and $n$ a.a.s.

Finally, to see that $D_0 \cup D(n,C/n)$ contains a cycle of length $2$ a.a.s., simply observe that $D_0$ has at least $\alpha n^2$ directed edges, and so the probability no edge of $D(n,C/n)$ is in the opposite orientation of an edge of $D_0$ is at most

\begin{equation*} (1-C/n)^{\alpha n^2} \leq e^{- C\alpha n}.\end{equation*}

6. The total degree absorbing lemma

While following the same general outline as the proof of Theorem 1.3, the proof of Theorem 1.4 requires several more details in order to deal with complications arising from two sources. First, since the statement of Theorem 1.4 would be false if we relaxed it to a statement about arbitrary orientations of cycles, our proof needs to exploit the property that the cycles we wish to embed do not have $(1-o(1))n$ vertices of indegree $1$ . Second, the condition $\delta (D) \geq 2 \alpha n$ is only enough to give that $d^+(v) \geq \alpha n$ or $d^-(v) \geq \alpha n$ , but not necessarily both, for each vertex $v \in V(D)$ . After introducing some convenient notation, we redefine the global and local absorbers from Section 4 to fit our needs here. The statements of the absorbing lemma and helper lemmas are very similar to those in Section 4, of course with additional technicalities.

Let $P = (u_1, \dots, u_k)$ be an oriented path. Recall that we call $u_1$ the startpoint of $P$ and $u_k$ the endpoint of $P$ , and recall that $\sigma (u_i u_{i+1}) = +$ if $\overrightarrow{u_i u_{i+1}} \in E(P)$ and $\sigma (u_i u_{i+1}) = -$ otherwise. For $i \in [k-1]\setminus \{1\}$ , we call $u_i$ a swap vertex of $P$ if the indegree of $u_i$ in $P$ is $0$ or $2$ . At swap vertices, the directions of the edges of an oriented path change from forwards to backwards, or vice versa. Note that the ‘type’ of swap vertices alternate along the path between indegree $0$ and $2$ . Recall that when the endpoint of $P$ is the startpoint of $P'$ and the oriented paths $P$ and $P'$ are otherwise vertex-disjoint, $P \circ P'$ denotes the concatenation of the two paths.

We cannot hope to find a copy of a given oriented path with prescribed startpoint and endpoint in a digraph $D$ unless those vertices have suitably high in- or outdegree in $D$ . This motivates the following two definitions.

Definition 6.1 ( $\alpha$ -compatible). Let $P = (u_1, \dots, u_k)$ be an oriented path, let $D$ be an $n$ -vertex digraph, and let $\alpha \gt 0$ . For $v_1,v_k \in V(D)$ , we say that $(v_1,v_k)$ is $\alpha$ -compatible with $P$ if $d^*(v_1) \geq \alpha n$ for $* = \sigma (u_1 u_2)$ and $d^*(v_k) \geq \alpha n$ for $* = \sigma (u_k u_{k-1})$ .

Definition 6.2 (Global absorber). Let $P$ be an oriented path, let $D$ be a digraph, and let $\alpha \gt 0$ . A subset $A \subseteq V(D)$ is a $(P,\alpha )$ -global absorber if for every $R \subseteq V(D) \setminus A$ such that $|R| + |A| = |V(P)|$ , and for every pair of distinct $v,v' \in R$ such that $(v,v')$ is $\alpha$ -compatible with $P$ , there is a copy of $P$ in $D[A \cup R]$ with startpoint $v$ and endpoint $v'$ .

As in Section 4, the global absorber will be constructed out of smaller units called local absorbers, defined in Definition 6.3. We use a slightly expanded definition of local absorber as compared to Definition 4.2 so that we have the added flexibility of specifying the endpoint of the local absorber.

Definition 6.3 (Local absorber). Let $P$ be an oriented path, $D$ be a digraph, $S \subseteq V(D)$ , and $z \in V(D) \setminus S$ . A triple $(A,v,v')$ is a $P$ -absorber for $(S,z)$ if

• $A \subseteq V(D) \setminus (S \cup \{z\})$ is a set of $|V(P)|-2$ vertices,

• $v,v' \in A$ , with $v \neq v'$ ,

• for every $s \in S$ , $D[A \cup \{s,z\}]$ contains a copy of $P$ with startpoint $v$ and endpoint $v'$ .

We call $v$ the startpoint and $v'$ the endpoint of the $P$ -absorber $(A,v,v')$ .

The next lemma guarantees the existence of local absorbers avoiding some small set of vertices – this ensures that all the local absorbers we find will be vertex-disjoint.

Lemma 6.4. Let $n,k, \ell \in \mathbb N$ and $\varepsilon,\alpha \gt 0$ so that $\frac{1}{n} \leq \varepsilon \leq \frac{\alpha }{8k}$ and $k \geq 3\ell +9$ . Let $D$ be an $n$ -vertex $\varepsilon n$ -bipseudorandom digraph with $\delta (D) \geq 2\alpha n$ . Let $U \subseteq V(D)$ so that $|U| \leq \alpha n/2$ , and let $v,v' \in V(D) \setminus U$ be distinct. Let $P$ be an arbitrary oriented path $P$ on $k$ vertices with at least $3\ell +7$ swap vertices such that $(v,v')$ is $\alpha$ -compatible with $P$ . For every $S \subseteq V(D) \setminus \{v,v'\}$ of size $\ell$ , and every vertex $z \in V(D) \setminus (S \cup \{v,v'\})$ , there exists a $P$ -absorber $(A,v,v')$ for $(S,z)$ disjoint from $U$ .

Proof. Let $P = (u_1, \dots, u_k)$ . Label $S \cup \{z\}$ as $z_1, \dots, z_{\ell +1}$ , where $z_{\ell +1} \;:\!=\; z$ . We will find a $P$ -absorber for $(S,z)$ by applying Lemma 3.3 to various neighbourhoods of the $z_i$ , $v$ and $v'$ . Let $*_i \;:\!=\; +$ if $d^+(z_i) \geq \alpha n$ , and let $*_i \;:\!=\; -$ otherwise. Choose $\ell +1$ swap vertices of $P$ , $u_{i_1}, \dots, u_{i_{\ell +1}}$ , such that

• $i_{j+1} - i_j \geq 2$ for $0 \leq j \leq \ell +1$ , where $i_0 \;:\!=\; 2$ and $i_{\ell +2} \;:\!=\; k-1$ ,

• $i_{\ell +1} - i_{\ell } \geq 3$ ,

• $d_P^{*_j}(u_{i_j}) = 2$ for every $j \in [\ell +1]$ .

This is possible because $P$ has at least $3\ell +7$ swap vertices, and they alternate having in- or outdegree $2$ . Define

• $B_1\;:\!=\; N^*(v)$ , where $* = \sigma (u_1 u_2)$ ,

• $B_{i_j-2} \;:\!=\; B_{i_j-1} \;:\!=\; N^{*_j}(z_j)$ for $j \in [\ell ]$ ,

• $B_{i_{\ell +1}-3} \;:\!=\; B_{i_{\ell +1}-2} \;:\!=\; N^{*_{\ell +1}}(z_{\ell +1})$ ,

• $B_{k-4} \;:\!=\; N^*(v')$ , where $* = \sigma (u_k u_{k-1})$ ,

• $B_i \;:\!=\; V(D)$ for all remaining $i\in [k-4]$ .

Since $(v,v')$ is $\alpha$ -compatible with $P$ , and by the definition of the $*_j$ , we have that $|B_i| \geq \alpha n$ for every $i \in [k-4]$ . Since $|U| \leq \alpha n/2$ , there exists pairwise disjoint subsets $B'_{\!\!i} \subseteq B_i\setminus (U \cup S \cup \{z\})$ such that for all $i \in [k-4]$ ,

\begin{equation*}|B'_{\!\!i}| \geq \frac {(\alpha n- \alpha n/2 -\ell -1)}{(k-4)} \geq \frac {\alpha n}{4(k-4)} \geq 2 \varepsilon n.\end{equation*}

Lemma 3.3 gives a bidirected path $(v_1, \dots, v_{k-4})$ in $D$ with $v_i \in B' _i$ for every $i \in [k-4]$ . Let $A \;:\!=\; \{v, v_1, \dots, v_{k-4}, v'\}$ , and note that $A$ is disjoint from $U$ and $S \cup \{z\}$ .

To see that $A$ is a $P$ -absorber for $(S,z)$ , note that for every $z_j \in S$ , the path

\begin{equation*} (v, v_1, \dots, v_{i_j-2}, z_j, v_{i_j-1}, \dots, v_{i_{\ell +1}-3}, z, v_{i_{\ell +1}-2}, \dots, v_{k-4}, v') \end{equation*}

is a copy of $P$ in $D[A \cup \{z_j,z\}]$ with startpoint $v$ and endpoint $v'$ ; see Figure 4.

Our global absorber is structured and operates similarly to the global absorber in Section 4: given a set $R$ of vertices we wish to absorb, we first absorb $R$ using some vertices from a specific set $X$ of vertices, whose properties are given in Definition 6.6; the rest of the global absorber absorbs what is left of $X$ using carefully constructed local absorbers. The existence of an appropriate $X$ is given by Lemma 6.7. Lemma 6.8 helps Lemma 6.9 to absorb $R$ using $X$ , and Lemma 6.11 is where we actually construct the global absorber.

First, we need the following simple observation.

Fact 6.5. Let $n \in \mathbb N$ and $\alpha \gt 0$ such that $2\alpha n+1 \leq n$ . Let $D$ be an $n$ -vertex digraph with $\delta (D) \geq 2\alpha n$ . Then there exists a partition $V^+ \cup V^-$ of $V(D)$ such that for each $* \in \{+,-\}$ we have that $|V^*| \geq \alpha n/2$ and $d^*(v) \geq \alpha n/2$ for every $v \in V^*$ .

Proof. Let $U^* \;:\!=\; \{v \in V(D) \;:\; d^*(v) \geq \alpha n/2\}$ for each $* \in \{+,-\}$ . Since $\delta (D) \geq 2\alpha n$ , we have that

\begin{equation*} \frac {\alpha n}{2} (n-|U^*|) + n|U^*| \geq |E(D)| \geq \alpha n^2,\end{equation*}

which yields $|U^*| \geq \alpha n/2$ for each $* \in \{+,-\}$ . Since $\delta (D) \geq 2\alpha n$ , $U^+\cup U^-= V(D)$ .

If $|U^+ \setminus U^-| \geq \alpha n/2$ , then $V^+ \;:\!=\; U^+ \setminus U^-$ and $V^- \;:\!=\; U^-$ is a desired partition of $V(D)$ . Similarly, we get the desired partition if $|U^- \setminus U^+| \geq \alpha n/2$ .

Figure 4. An example of a $P$ -absorber $(A,v,v')$ for $(S=\{s_1,s_2\},z)$ from Lemma 6.4. The double edges indicate that both orientations are present. Notice that $u_4, u_7, u_{10}$ are swap vertices of $P$ , and for each fixed $i\in \{1,2\}$ , $A \cup \{s_i, z\}$ contains a copy of $P$ with startpoint vertex $v$ and endpoint $v'$ in which vertex $z$ plays the role of $u_{10}$ , and either $s_1$ plays the role of $u_4$ or $s_2$ plays the role of $u_7$ .

Otherwise, we must have that $|U^+ \cap U^-|\geq n-\alpha n \geq \alpha n +1$ . In this case, we partition $U^+ \cap U^-$ into $A \cup B$ with $||A| - |B|| \leq 1$ and set $V^+ \;:\!=\; (U^+ \setminus U^-) \cup A$ and $V^- \;:\!=\; (U^- \setminus U^+) \cup B$ .

Definition 6.6. Let $n \in \mathbb N$ and $\alpha, \beta \gt 0$ . Let $D$ be an $n$ -vertex digraph. We call $X \subseteq V(D)$ an $(\alpha,\beta,m)$ -reservoir if

• • $|X| = (1+\beta )m$ , where $m$ and $\beta m$ are both integers;

• • for every $v \in V(D)$ and for every $* \in \{+,-\}$ , if $d^*(v) \geq \alpha n/ 2$ , then $|N^*(v) \cap X| \geq 2\beta m$ ;

• • there is a partition $X^+$ , $ X^-$ of $X$ such that $|X^+|, |X^-| \geq 2\beta m$ , and for each $* \in \{+,-\}$ we have that $d^*(v) \geq \alpha n/2$ for every $v \in X^*$ .

Lemma 6.7. Let $\alpha, \beta \gt 0$ such that $2\beta \leq \alpha/3 \leq 1/9$ , and let $m,n \in \mathbb N$ such that $\beta m \in \mathbb N$ , $n$ is sufficiently large, and $\log n \ll m \leq 0.9 n$ . Let $D$ be an $n$ -vertex digraph with $\delta (D) \geq 2\alpha n$ . Then there exists an $(\alpha,\beta,m)$ -reservoir in $D$ .

Proof. By Fact 6.5, there exists a partition $V^+, V^-$ of $V(D)$ such that for each $* \in \{+,-\}$ we have that $|V^*| \geq \alpha n/2$ and $d^*(v) \geq \alpha n/2$ for every $v \in V^*$ .

Let $X$ be a randomly selected subset of $V(D)$ of size $(1+\beta )m$ . Set $X^+ \;:\!=\; V^+\cap X$ and $ X^-\;:\!=\; V^-\cap X$ . Then by the Chernoff bound for the hypergeometric distribution, with positive probability the following hold: for every $v \in V(D)$ and for each $* \in \{+,-\}$ , $d^*(v) \geq \alpha n/2$ implies $|N^*(v) \cap X| \geq \alpha m/ 3 \geq 2 \beta m$ ; $|X^+ |, |X^-| \geq 2 \beta m$ . Thus, $X$ is an $(\alpha,\beta,m)$ -reservoir, as desired.

Lemma 6.8. Let $\alpha, \beta, \varepsilon \gt 0$ and $k, m, n \in \mathbb N$ so that $\beta m/6 \geq 2 \varepsilon n$ and $4 \leq k \leq \frac{3}{2} \beta m$ . Let $P$ be an oriented path on $k$ vertices. Let $D$ be an $n$ -vertex $\varepsilon n$ -bipseudorandom digraph with $\delta (D) \geq 2\alpha n$ such that $D$ has an $(\alpha,\beta,m)$ -reservoir $X$ . For every distinct $v,v' \in V(D) \setminus X$ such that $(v,v')$ is $(\alpha/2)$ -compatible with $P$ , and for every $U \subseteq X$ with $|U| + k \leq \frac{3}{2} \beta m$ , there exists a copy of $P$ in $D[(X \setminus U) \cup \{v,v'\}]$ with startpoint $v$ and endpoint $v'$ .

Proof. Let $X^+$ , $X^-$ be the partition of $X$ as given in Definition 6.6. Let $P = (u_1, \dots, u_k)$ . Fix an arbitrary $U \subseteq X$ with $|U| + k \leq \frac{3}{2} \beta m$ , and let $v_1, v_k \in V(D) \setminus X$ be such that $(v_1, v_k)$ is $(\alpha/2)$ -compatible with $P$ . We will construct a copy $Q = (v_1, \dots, v_k)$ of $P$ in $D[(X \setminus U) \cup \{v_1, v_k\}]$ in stages, in all but the final step adding two vertices at a time.

For some $i \leq (k-2)/2$ , assume that there is a copy $Q^{\leq 2i-1} = (v_1, \dots, v_{2i-1})$ of $(u_1, \dots, u_{2i-1})$ in $D[(X\setminus U) \cup \{v_1\}]$ such that $d^*(v_{2i-1}) \geq \alpha n/2$ , where $* = \sigma (u_{2i-1} u_{2i})$ . Note that $Q^{\leq 1}\;:\!=\; (v_1)$ satisfies this for $i=1$ . Let $B_1 \;:\!=\; N^*(v_{2i-1}) \cap X$ for $* = \sigma (u_{2i-1} u_{2i})$ and $B_2 \;:\!=\; X^*$ for $* = \sigma (u_{2i+1} u_{2i+2})$ . Since $|B_1|, |B_2| \geq 2\beta m$ and $|U \cup V(Q^{\leq 2i-1})| \leq |U| + k \leq \frac{3}{2} \beta m$ , there exist disjoint subsets $B'_{\!\!i} \subseteq B_i$ of size at least $\beta m/4 \geq \varepsilon n$ disjoint from $U$ and $V(Q^{\leq 2i-1})$ . Since $D$ is $\varepsilon n$ -bipseudorandom, there exists $v_{2i} \in B'_{\!\!1}$ and $v_{2i+1} \in B'_{\!\!2}$ such that $(v_{2i-1}, v_{2i}, v_{2i+1})$ is a copy of $(u_{2i-1}, u_{2i}, u_{2i+1})$ . We thus obtain $Q^{\leq 2i+1} \;:\!=\; Q^{\leq 2i-1} \circ (v_{2i-1}, v_{2i}, v_{2i+1})$ as a copy of $(u_1, \dots, u_{2i+1})$ in $D[(X \setminus U) \cup \{v_1\}]$ with $d^*(v_{2i+1}) \geq \alpha n/2$ for $* = \sigma (u_{2i+1} u_{2i+2})$ .

If $k$ is even, then we slightly modify the last step, after constructing $Q^{\leq k-3}$ . Similarly as before, we can find a bidirected edge $\overleftrightarrow{v_{k-2} v_{k-1}}$ between $N^*(v_{k-3}) \cap X$ with $* = \sigma (u_{k-3} u_{k-2})$ and $N^*(v_k) \cap X$ with $* = \sigma (u_k u_{k-1})$ disjoint from $U \cup V(Q^{\leq k-3})$ . Thus $Q \;:\!=\; Q^{\leq k-3} \circ (v_{k-3}, v_{k-2}, v_{k-1}, v_k)$ contains a copy of $P$ with startpoint $v_1$ , endpoint $v_k$ , and all internal vertices in $X \setminus U$ .

If $k$ is odd, then we construct $Q^{\leq k-4}$ and use Lemma 3.3 in place of the pseudorandom property. Let $B_1 \;:\!=\; N^*(v_{k-4}) \cap X$ for $* = \sigma (u_{k-4} u_{k-3})$ , $B_2\;:\!=\; X$ , and $B_3\;:\!=\; N^*(v_k) \cap X$ with $* = \sigma (u_k u_{k-1})$ . Since $|B_1|, |B_2|, |B_3| \geq 2\beta m$ and $|U \cup V(Q^{\leq k-4})| \leq \frac{3}{2} \beta m$ , there exists disjoint subsets $B'_{\!\!i} \subseteq B_i$ of size at least $\beta m/6 \geq 2\varepsilon n$ disjoint from $U$ and $V(Q^{\leq k-4})$ . By Lemma 3.3, there exists a bidirected path $(v_{k-3}, v_{k-2}, v_{k-1})$ with $v_{k-3} \in B_1$ , $v_{k-2} \in B_2$ , and $v_{k-1} \in B_3$ . Thus $Q \;:\!=\; Q^{\leq k-4} \circ (v_{k-4}, v_{k-3}, v_{k-2}, v_{k-1}, v_k)$ contains a copy of $P$ with startpoint $v_1$ , endpoint $v_k$ , and all internal vertices in $X \setminus U$ .

Lemma 6.9. Let $\alpha, \beta, \varepsilon \gt 0$ and $m, n \in \mathbb N$ so that $\beta m/6 \geq 2 \varepsilon n$ . Let $D$ be an $n$ -vertex $\varepsilon n$ -bipseudorandom digraph with $\delta (D) \geq 2\alpha n$ , and suppose that $D$ has an $(\alpha,\beta,m)$ -reservoir $X$ . Let $R \subseteq V(D) \setminus X$ so that $|R|\geq 2$ , and let $v, v' \in R$ be distinct. Let $P$ be an oriented path on $|R| + \beta m$ vertices containing at least $4|R|-6$ swap vertices. If $(v,v')$ is $(\alpha/2)$ -compatible with $P$ , then there exists a copy of $P$ in $D[R \cup X]$ with startpoint $v$ and endpoint $v'$ that covers $R$ .

Note that if $P$ has $|R| + \beta m$ vertices and at least $4|R|-6$ swap vertices, then $|R| \leq \frac{1}{3} (\beta m + 4)$ . This implies that $P$ has less than $\frac{3}{2}\beta m$ vertices, which allows us to use Lemma 6.8.

Proof. Label $R$ as $\{v_1, \dots, v_\ell \}$ , with $v \;=\!:\; v_1$ and $v' \;=\!:\; v_\ell$ . Set $k \;:\!=\; \beta m + \ell$ and write $P = (u_1, \dots, u_k)$ . So $P$ contains at least $4\ell -6$ swap vertices and $(v_1, v_\ell )$ is $(\alpha/2)$ -compatible with $P$ .

Choose $\ell -2$ swap vertices of $P$ , $u_{i_2}, \dots, u_{i_{\ell -1}}$ , such that

• $i_{j+1} - i_j \geq 3$ for $j \in [\ell -1]$ , where $i_1 \;:\!=\; 1$ and $i_{\ell }\;:\!=\; k$ ,

• $d^*(v_j) \geq \alpha n$ with $* = \sigma (u_{i_j} u_{i_j+1})$ , for every $2 \leq j \leq \ell -1$ .

This is possible because $P$ has at least $4\ell -6$ swap vertices, and they alternate having in- or outdegree $2$ . Let $P_j \;:\!=\; (u_{i_j}, \dots, u_{i_{j+1}})$ for $j \in [\ell -1]$ , and observe that $(v_j, v_{j+1})$ is $(\alpha/2)$ -compatible with $P_j$ . Since the number of vertices used in total is at most $|P| \leq \frac{3}{2} \beta m$ , by Lemma 6.8, we can find pairwise internally disjoint copies $Q_j$ of $P_j$ in $D[X \cup \{v_j, v_{j+1}\}]$ with startpoint $v_j$ and endpoint $v_{j+1}$ . Concatenating the $Q_j$ as $Q \;:\!=\; Q_1 \circ \cdots \circ Q_{\ell -1}$ , we obtain a copy of $P$ in $D[R \cup X]$ with startpoint $v_1$ and endpoint $v_{\ell }$ covering $R$ ; see Figure 5.

Before proving the main absorbing lemma, we need a lemma which allows us to construct long paths with endpoints that are compatible with a given short path. This is useful in the construction of the global absorber and in the application of the global absorber in Section 7.

Lemma 6.10. Let $n \in \mathbb N$ and $0\lt \varepsilon, \alpha \lt 1/3$ such that ${1}/{n} \leq \varepsilon \leq \alpha/32$ . Let $D$ be an $n$ -vertex $\varepsilon n$ -bipseudorandom digraph with $\delta (D) \geq 2\alpha n$ , and let $U \subseteq V(D)$ with $|U| \leq \alpha n/4$ . For every $2 \leq k \leq (1-8\varepsilon )n - |U|$ and for every $(*_1, *_2) \in \{+,-\}^2$ , there exists a bidirected path on $k$ vertices in $D \setminus U$ with startpoint $v$ and endpoint $v'$ satisfying $d^{*_1}_D(v), d^{*_2}_D(v') \geq \alpha n/2$ .

Proof. Fix $k \leq (1-8\varepsilon )n - |U|$ , $*_1$ , and $*_2$ . By Fact 6.5, and as $|U| \leq \alpha n/4$ , we can partition $V(D) \setminus U$ as $V^+ \cup V^-$ , where for each $* \in \{+,-\}$ we have that $|V^*| \geq \alpha n/4$ , and $d^*_D(v) \geq \alpha n/2$ for every $v \in V^*$ . Lemma 3.4 gives a bidirected path $Q^*$ in $D[V^*]$ on at least $|V^*| - 2\varepsilon n$ vertices for each $* \in \{+,-\}$ .

Case 1: $*_1 \neq *_2$ . We take the last $\varepsilon n$ vertices of $Q^-$ and the first $\varepsilon n$ vertices of $Q^+$ and find a bidirected edge between them, which exists since $D$ is $\varepsilon n$ -bipseudorandom. This gives a bidirected path $Q$ on at least $|V(Q^-)| + |V(Q^+)| - 2 \varepsilon n \geq n - |U| -6\varepsilon n$ vertices. Truncating $Q$ at both ends, we obtain a bidirected path on $k$ vertices with startpoint in $V^{*_1}$ and endpoint in $V^{*_2}$ .

Figure 5. A copy of $P$ in $D[R\cup X]$ with startpoint $v_1$ and endpoint $v_\ell$ that covers all the vertices in $R$ , as found in Lemma 6.9. The path between $v_i$ and $v_{i+1}$ is found by Lemma 6.8. The double edges indicate that both orientations are present, as found by applying the bipseudorandom property.

Case 2: $*_1 = *_2$ . Without loss of generality, assume $*_1 = *_2 = +$ . If $k \leq |V(Q^+)|$ , simply truncate $Q^+$ to $k$ vertices to obtain the desired path. If $k \gt |V(Q^+)|$ , then truncate $Q^-$ to $Q^-_1$ on $k-|V(Q^+)|+ 4\varepsilon n \geq 2\varepsilon n$ vertices, which is possible because

\begin{equation*} k - |V(Q^+)| + 4\varepsilon n \leq (1-8\varepsilon )n - |U| - (|V^+|-2\varepsilon n) + 4\varepsilon n = |V^-| - 2 \varepsilon n \leq |V(Q^-)| .\end{equation*}

Between the first $\varepsilon n$ vertices of $Q^-_1$ and the first $\varepsilon n$ vertices of $Q^+$ we find a bidirected edge, as well as between the last $\varepsilon n$ vertices of $Q^-_1$ and the ‘second’ $\varepsilon n$ vertices of $Q^+$ . This yields a bidirected path $Q$ on at least $k$ vertices and at most $k + 4\varepsilon n$ vertices with startpoint and endpoint in $V^+$ . Since

\begin{equation*} |V(Q^+)| \geq |V^+| - 2\varepsilon n \geq \alpha n/4 - 2\varepsilon n \geq 6\varepsilon n,\end{equation*}

we may truncate $Q$ to $k$ vertices and still have the startpoint and endpoint in $V^+$ .

We are now ready to prove the absorbing lemma for Theorem 1.4.

Lemma 6.11 (Absorbing lemma). For every $0\lt \alpha, \eta \ll 1$ , and every $0\lt \varepsilon \leq \alpha ^2 \eta ^4/10^8$ , there exists an $n_0 \in \mathbb N$ such that for all $n \geq n_0$ the following holds. Let $D$ be an $n$ -vertex $\varepsilon n$ -bipseudorandom digraph with $\delta (D) \geq 2\alpha n$ . Let $P$ be an oriented path on $\lceil{\alpha n/4}\rceil$ vertices with at least $\eta (|V(P)|-2)$ swap vertices. Then $D$ contains a $(P,\alpha/2)$ -global absorber of size at most ${\lceil{\alpha n/4}\rceil } - 9\varepsilon n$ .

Proof. Let $n$ be chosen sufficiently large so that all our calculations will hold. Let $D$ and $P$ be as in the statement of the lemma. We first construct the global absorber and then prove that it is indeed a $(P,\alpha/2)$ -global absorber. Define $\beta, m \gt 0$ such that $\alpha/7 \leq \beta \leq \alpha/6$ and $\frac{\alpha \eta ^3}{50000} n \leq m \leq \frac{\alpha \eta ^3}{49999} n$ , and so that $m$ and $\beta m$ are integers. Without loss of generality, we may assume that $516/\eta$ is an integer.

Let $X$ be an $(\alpha,\beta,m)$ -reservoir, whose existence is guaranteed by Lemma 6.7. Let $Y, Z \subseteq V(D) \setminus X$ be disjoint sets of $2m$ and $3m$ vertices, respectively. Fix an auxiliary graph $H_m$ isomorphic to the graph from Lemma 4.6 on $X \cup Y \cup Z$ . For each $z \in Z$ , we set $N_z \;:\!=\; N_{H_m}(z)$ .

We split $P$ into several pieces as follows. Let $P = (u_1, \dots, u_k)$ , with $k\;:\!=\;{\lceil{\alpha n/4}\rceil }$ . Set $r\;:\!=\; 9 \varepsilon n$ and $\ell \;:\!=\; \beta m + r - 4$ . Define

• $P^0 \;:\!=\; (u_1, u_2, u_3, u_4)$ ,

• $P^1 \;:\!=\; (u_4, \dots, u_{j+1})$ ,

• $P^2 \;:\!=\; (u_{j+1}, \dots, u_{j+\ell })$ ,

• $P^3 \;:\!=\; (u_{j+\ell }, \dots, u_{k-3})$ ,

• $P^4 \;:\!=\; (u_{k-3}, u_{k-2}, u_{k-1}, u_k)$ ,

where $4 \leq j \leq k-4-\ell$ is chosen so that $P^2$ has at least $4r - 6$ swap vertices. This is possible because otherwise there are at most

(6.1) \begin{align} \left \lfloor \frac{k-10}{\ell }\right \rfloor (4r-5) + (\ell -1) +8 \lt 12 \frac{\alpha n}{\beta m} \varepsilon n + \beta m + 9\varepsilon n \lt \eta (k-2)n \end{align}

swap vertices of $P$ , a contradiction. To see where (6.1) comes from, one should consider a partition of $V(P)\setminus \{u_1,\dots, u_5, u_{k-4},\dots, u_k\}$ into $\left \lfloor \frac{k-10}{\ell }\right \rfloor$ sets of $\ell$ consecutive vertices along $P$ , and one ‘leftover’ set of size at most $\ell -1$ . One should also note that it is only the internal vertices along a path that can be swap vertices; this is why (6.1) has a $4r-5$ term rather than a $4r-7$ term.

We claim that for some $i=1,3$ we have that $P^i$ has at least $6192m/\eta ^2$ vertices, and at least $\eta |V(P^i)|/2$ of those vertices are swap vertices of $P^i$ . This is because if $P^1$ has fewer than $6192m/\eta ^2$ vertices, then $P^3$ must have at least

\begin{equation*} \eta (k-2) - 10 - \ell - 6192m/\eta ^2 \geq \max \left \{ \frac {\eta }{2} k, 6192m/\eta ^2 \right \} \end{equation*}

swap vertices; if $P^1$ has less than an $\eta/2$ -proportion of its vertices being swap vertices, then $P^3$ must have at least

\begin{equation*} \eta (k-2) - 10 - \ell - \frac {\eta }{2} j \geq \max \left \{\frac {\eta }{2} |V(P^3)|, 6192m/\eta ^2\right \} \end{equation*}

swap vertices. Assume that our claim held for $i=1$ ; the $i=3$ case follows by an essentially identical argument with $P^3$ in place of $P^1$ .

Our local absorbers will be ‘housed’ in $P^1$ ; the segment $P^2$ will be used to absorb $R$ from Definition 6.2; $P^0$ and $P^4$ are used to ensure the copy of $P$ we find has the correct startpoint and endpoint; $P^3$ is simply used to fill up the remaining part of $P$ .

Let $p \;:\!=\; 516/\eta$ (recalling that $p$ is an integer) and $s \;:\!=\; \lfloor{\frac{j-8}{p}}\rfloor -1$ . For $0 \leq i \leq s$ , define $P^1_i \;:\!=\; (u_{ip+5}, \dots, u_{(i+1)p+4})$ ; see Figure 6. We call $P^1_i$ good if it contains at least $3 \cdot 40 + 7 = 127$ swap vertices of $P^1_i$ ; this will be enough to apply Lemma 6.4 later to find a local absorber for $(N_z,z)$ .

Figure 6. The pieces $P^i$ which compose the path $P$ as in the proof of Lemma 6.11. $P^1$ has at least $6192m/\eta ^2$ vertices and at least an $\eta/2$ -proportion of those vertices are swap vertices, while $P^2$ has at least $4r -6$ swap vertices. We further divide $P^1$ into disjoint $P^1_i$ of equal length which house the local absorbers.

Note that there must be at least $3m$ good $P^1_i$ , since otherwise $P^1$ has at most

(6.2) \begin{align} (s+1) \cdot 128 + (3m-1) \cdot p + (j-2-(s+1)p) \lt 129 (s+1) + 3mp \leq \frac{\eta }{2} |V(P^1)| \end{align}

swap vertices, a contradiction. Note that the first term in (6.2) is $(s+1) \cdot 128$ as, including the startpoint and endpoint of $P^1_i$ , $V(P^1_i)$ may contain at most $128$ swap vertices of $P^1$ , and yet only contain at most $126$ swap vertices of $P^1_i$ . The second term in (6.2) corresponds to the $P^1_i$ s in which every vertex may be a swap vertex of $P^1$ . The third term in (6.2) counts all those vertices on $P^1$ that do not live in one of the $P^1_i$ . The final inequality in (6.2) follows as $\frac{\eta }{4} |V(P^1)| \geq 3mp$ (as $|V(P^1)|\geq 6192m/\eta ^2$ and $p= 516/\eta$ ), and as $129(s+1) \leq 129 \frac{j-2}{p} = \frac{\eta }{4} |V(P^1)|$ (by the definition of $s$ and $p$ ).

As $|X\cup Y\cup Z|\leq \alpha n/6$ , Fact 6.5 ensures a partition $V^+, V^-$ of $V(D) \setminus (X \cup Y \cup Z)$ such that $|V^*| \geq{\alpha }n/3$ and $d^*_D(v) \geq \alpha n/2$ for every $v \in V^*$ and $* \in \{+,-\}$ . Since $D$ is $\varepsilon n$ -bipseudorandom, we can find pairwise disjoint bidirected edges $\overleftrightarrow{w_i w'_{\!\!i}}$ for $0 \leq i \leq s+1$ , where $w_i \in V^*$ with $* = \sigma (u_{ip+4} u_{ip+3})$ and $w_i' \in V^*$ with $* = \sigma (u_{ip+5} u_{ip+6})$ . In this way, $(w_i', w_{i+1})$ is $(\alpha/2)$ -compatible with $P^1_i$ for $0 \leq i \leq s$ .

As there are at least $3m$ good $P^1_i$ , we can assign to each $z \in Z$ a distinct $i_z$ such that $P^1_{i_z}$ is good. We construct pairwise disjoint $P^1_{i_z}$ -absorbers $(A_{i_z}, w'_{\!\!i_z}, w_{i_z+1})$ for $(N_z,z)$ , disjoint from $X \cup Y \cup Z$ , via repeated applications of Lemma 6.4; this is possible as $\varepsilon \leq \frac{\alpha }{8p}$ , and because in the process of constructing these local absorbers we use at most $3mp\leq \alpha n/4$ vertices in total.

Let $I \;:\!=\; \{ i \;:\; 0 \leq i \leq s, \nexists z \in Z \text{ with } i = i_z\}$ . For each $i \in I$ , we find a copy $Q^1_i$ of $P^1_i$ with startpoint $w_i'$ and endpoint $w_{i+1}$ such that they are pairwise disjoint and disjoint from $X \cup Y \cup Z$ and $A_{i_z}$ for all $z \in Z$ . This is achieved by applying Lemma 3.3 as follows. Let $B_2 \;:\!=\; N^*_D(w_i')$ for $* = \sigma (u_{ip+5} u_{ip+6})$ and $B_{p-1} \;:\!=\; N^*_D(w_{i+1})$ for $* = \sigma (u_{(i+1)p+4} u_{(i+1)p+3})$ , and note that $|B_2|, |B_{p-1}| \geq \alpha n/2$ . Let $B'_{\!\!2} \subseteq B_2$ and $B'_{\!\!p-1} \subseteq B_{p-1}$ be disjoint from each other and all the vertices in $X \cup Y \cup Z$ , $\bigcup _{z\in Z} A_{i_z}$ , and the other $Q^1_i$ , of which there are at most $k ={\lceil{\alpha n/4}\rceil }$ , so that $|B'_{\!\!2}|, |B'_{\!\!p-1}| \geq \alpha n/ 10 \geq 2\varepsilon n$ . Let $B_3', \dots, B_{p-2}'$ be arbitrary pairwise disjoint subsets of $V(D)$ of size at least $2\varepsilon n$ , disjoint from everything from before. By Lemma 3.3 there is a bidirected path through the $B'_{\!\!i}$ ; adding $w_i'$ and $w_{i+1}$ on either end gives the desired $Q^1_i$ .

Finally for $P^1$ , we find a bidirected edge $\overleftrightarrow{w_{s+2} w'_{\!\!s+2}}$ disjoint from $X \cup Y \cup Z$ , the $Q^1_i$ for $i \in I$ , and the local absorbers $A_{i_z}$ , with the property that $w_{s+2} \in V^*$ with $* = \sigma (u_{j} u_{j-1})$ and $w'_{\!\!s+2} \in V^*$ with $* = \sigma (u_{j+1} u_{j+2})$ . In a similar fashion as before, since $(w_{s+1}', w_{s+2})$ is $(\alpha/2)$ -compatible with $(u_{(s+1)p+5}, \dots, u_j)$ , we find a copy $Q^1_{s+1}$ of $(u_{(s+1)p+5}, \dots, u_j)$ with startpoint $w_{s+1}'$ and endpoint $w_{s+2}$ .

Let

\begin{equation*} A^1 \;:\!=\; \{w_0\} \cup \bigcup _{z \in Z} A_{i_z} \cup \bigcup _{i\in I} V(Q^1_i) \cup V(Q^1_{s+1}) \cup \{w'_{\!\!s+2}\}, \end{equation*}

then

(6.3) \begin{equation} |A^1| = 1 + 3m(p-2) + (s+1-3m)p + (j-(s+1)p-4) + 1 = j - 6m - 2 =|V(P^1)|-6m. \end{equation}

Claim 6.12. Given any matching in $H_m$ covering $Z$ , let $Z' \subseteq X \cup Y$ denote the set of vertices matched to $Z$ . Then there exists a copy of $P^1$ in $D[A^1 \cup Z \cup Z']$ with startpoint $w_0$ and endpoint $w'_{\!\!s+2}$ .

Proof. For each $z \in Z$ , we activate the local absorber $A_{i_z}$ for $z$ and its matched vertex $z'$ in $Z'$ , yielding a copy $Q^1_{i_z}$ of $P^1_{i_z}$ containing $z$ and $z'$ . We concatenate the $Q^1_i$ to obtain a copy of $P^1$ as

\begin{equation*} (w_0, w'_{\!\!0}) \circ Q^1_0 \circ (w_1, w'_{\!\!1}) \circ Q^1_1 \circ \cdots \circ Q^1_{s+1} \circ (w_{s+2}, w'_{\!\!s+2}) \end{equation*}

with startpoint $w_0$ and endpoint $w'_{\!\!s+2}$ ; see Figure 7.

Figure 7. A copy of $P^1$ in $D[A^1 \cup Z \cup Z']$ as found in Claim 6.12. The $w_i w'_{\!\!i}$ edges are double edges, as found by applying the bipseudorandom property to $V^+$ and $V^-$ .

To complete the construction of the global absorber, we use Lemma 6.10 to obtain a copy $Q^3$ of $P^3$ disjoint from $A^1 \cup X \cup Y \cup Z$ with startpoint $w \in V^*$ where $* = \sigma (u_{j+\ell } u_{j+\ell -1})$ , and endpoint $w' \in V^*$ where $* = \sigma (u_{k-3} u_{k-2})$ . Let

\begin{equation*} A\;:\!=\; X \cup Y \cup Z \cup A^1 \cup V(Q^3) .\end{equation*}

By (6.3), $\ell = \beta m + r - 4$ , $r = 9\varepsilon n$ , and $k ={\lceil{\alpha n/4}\rceil }$ , we have that

\begin{equation*} |A| = (6+\beta )m + (j-6m-2) + (k-2-j-\ell ) = k - r = {\lceil {\alpha n/4}\rceil } - 9\varepsilon n. \end{equation*}

Now we prove that $A$ is indeed a $(P,\alpha/2)$ -global absorber. Let $R \subseteq V(D) \setminus A$ with $|R| + |A| = |V(P)|$ be given, as well as $v,v' \in R$ which are $\alpha/2$ -compatible with $P$ . Let $R' \;:\!=\; (R \setminus \{v,v'\}) \cup \{w'_{\!\!s+2}, w\}$ . By Lemma 6.9, there exists a copy $Q^2$ of $P^2$ in $D[R' \cup X]$ covering $R'$ with startpoint $w'_{\!\!s+2}$ and endpoint $w$ . By Lemma 6.8, there exists a copy $Q^0$ of $P^0$ in $D[X \cup \{v,w_0\}]$ disjoint from $V(Q^2)$ with startpoint $v$ and endpoint $w_0$ ; similarly, there exists a copy $Q^4$ of $P^4$ in $D[X \cup \{w', v'\}]$ disjoint from $V(Q^0)$ and $V(Q^2)$ with startpoint $w'$ and endpoint $v'$ .

Let $X'$ be the set of vertices in $X$ not used in $Q^0$ , $Q^2$ , or $Q^4$ . Thus,

\begin{equation*} |X'| = |X| - (2 + |V(P_2)| - |R'| + 2) = (1+\beta )m - \ell + r - 4 = m .\end{equation*}

By Lemma 4.6, there exists a perfect matching between $Z$ and $X' \cup Y$ . By Claim 6.12, there exists a copy $Q^1$ of $P^1$ with startpoint $w_0$ and endpoint $w'_{\!\!s+2}$ covering $X' \cup Y \cup Z \cup A^1$ . Concatenate the $Q^i$ as

\begin{equation*} Q \;:\!=\; Q^0 \circ Q^1 \circ Q^2 \circ Q^3 \circ Q^4 .\end{equation*}

Then $Q$ is a copy of $P$ in $D[R \cup A]$ with startpoint $v$ and endpoint $v'$ .

7. Proof of Theorem 1.4

Proof. To prove Theorem 1.4 it clearly suffices to prove the case when $\eta = \alpha$ and $0\lt \alpha \ll 1$ . Set $\varepsilon \;:\!=\; \alpha ^6/10^9$ and $C \;:\!=\; 4e/\varepsilon ^2$ , and let $n \in \mathbb N$ be sufficiently large. Let $D_0$ be an $n$ -vertex digraph with $\delta (D_0) \geq 2\alpha n$ .

Call an oriented cycle good if it has length between $3$ and $n$ with at most $(1-\alpha )n$ vertices of indegree $1$ , and it is not a consistently oriented cycle of length $3$ .

Given any good cycle $\mathcal{C}$ , we first prove that $D \;:\!=\; D_0 \cup D^*(n,C/n)$ contains a copy of $\mathcal C$ with probability at least $1 - e^{-n}$ . Note that Lemma 3.5 implies that $D^*(n,C/n)$ is $\varepsilon n$ -bipseudorandom with probability at least $1 - e^{-n}$ ; thus, we may assume that $D$ is an $\varepsilon n$ -bipseudorandom digraph.

When $|\mathcal{C}| = 3$ , then choose an arbitrary $v \in V(D)$ . Either $d^+_D(v) \geq \alpha n$ or $d^-_D(v) \geq \alpha n$ . In either case, since $\varepsilon \leq \alpha/2$ , we can find an edge in the in- or out-neighbourhood of $v$ using that $D$ is $\varepsilon n$ -bipseudorandom, yielding a non-consistently oriented cycle of length $3$ .

When $4 \leq |\mathcal{C}| \leq (1 - 13 \varepsilon/\alpha - 8 \varepsilon ) n$ , we first fix an $(\alpha/2, \alpha/12, \frac{12\varepsilon }{\alpha } n)$ -reservoir $X$ , as given by Lemma 6.7. In particular, $|X| \leq \frac{13\varepsilon }{\alpha } n \leq \alpha n/4$ , and for every $v \in V(D)$ and $* \in \{+,-\}$ , if $d^*_D(v) \geq \alpha n/4$ then $|N^*_D(v) \cap X| \geq 2 \varepsilon n$ . Let $(u_1, u_2, u_3, u_4)$ be a subpath of $\mathcal{C}$ . Since $|\mathcal{C}|-2 \leq (1-8\varepsilon )n-|X|$ , Lemma 6.10 gives us a bidirected path $Q_\leftrightarrow$ disjoint from $X$ on $|\mathcal{C}|-2$ vertices with startpoint $v$ and endpoint $v'$ satisfying $d^{*_1}_D(v), d^{*_2}_D(v') \geq \alpha n/4$ with $*_1 = \sigma (u_1 u_2)$ and $*_2 = \sigma (u_4 u_3)$ . We close $Q_\leftrightarrow$ into a copy of $\mathcal{C}$ by applying the bipseudorandom property to disjoint subsets of $N^{*_1}_D(v) \cap X$ and $N^{*_2}_D(v') \cap X$ .

When $|\mathcal{C}| \geq (1-13\varepsilon/\alpha -8\varepsilon ) n$ , we have at least $\alpha n - 13\varepsilon/\alpha n - 8\varepsilon n \geq 2\alpha n/3$ swap vertices in $\mathcal{C}$ . By a standard averaging argument, there is a subpath $P$ of $\mathcal{C}$ on $\lceil{\alpha n/4}\rceil$ vertices with at least $\frac{2\alpha }{3}(|V(P)|-2)$ swap vertices. By Lemma 6.11, there exists a $(P,\alpha/2)$ -global absorber $A$ of size at most ${\lceil{\alpha n/4}\rceil } - 9\varepsilon n$ . Let $P = (u_1, \dots, u_k)$ with $k \;:\!=\;{\lceil{\alpha n/4}\rceil }$ , and let $*_1 \;:\!=\; \sigma (u_1 u_2)$ and $*_2 \;:\!=\; \sigma (u_k u_{k-1})$ . By Lemma 6.10, there exists a bidirected path $Q_\leftrightarrow$ in $D \setminus A$ on $|\mathcal{C}| - k + 2 \leq n - |A| - 8\varepsilon n$ vertices with startpoint $v$ and endpoint $v'$ satisfying $d^{*_1}_D(v), d^{*_2}_D(v') \geq \alpha n/2$ . Let $R \subseteq V(D) \setminus (A \cup V(Q_\leftrightarrow ))$ be arbitrary with $|A| + |R| + 2 = k$ , which exists because

\begin{equation*} 0 \leq k-2-|A| = |\mathcal {C}| - |V(Q_\leftrightarrow )| - |A| \leq |V(D) \setminus (A \cup V(Q_\leftrightarrow ))| .\end{equation*}

Let $R' \;:\!=\; R \cup \{v,v'\}$ . Since $(v,v')$ is $(\alpha/2)$ -compatible with $P$ , $A$ is a $(P,\alpha/2)$ -global absorber, and $|A| + |R'| = |V(P)|$ , we have that $D[A \cup R']$ contains a copy $Q$ of $P$ with startpoint $v$ and endpoint $v'$ . Joining $Q$ and $Q_\leftrightarrow$ at both ends, we have a copy of $\mathcal{C}$ as desired.

Thus for every good cycle $\mathcal{C}$ , we have that $D_0 \cup D^*(n,C/n)$ contains a copy of $\mathcal{C}$ with probability at least $1-e^{-n}$ . Hence Lemma 3.1 implies that $D_0 \cup D(n,C/n)$ contains a copy of $\mathcal{C}$ with probability at least $1-e^{-n}$ . Taking a union bound over all the at most $n 2^n$ possible lengths and orientations, we have that $D_0 \cup D(n,C/n)$ contains every good oriented cycle a.a.s.

Finally, we deal with consistently oriented cycles of length $2$ and $3$ . To see that $D_0 \cup D(n,C/n)$ contains a cycle of length $2$ a.a.s., we proceed as in the proof of Theorem 1.3: observe that $D_0$ has at least $\alpha n^2$ directed edges, and so the probability no edge of $D(n,C/n)$ is in the opposite orientation of an edge of $D_0$ is at most

\begin{equation*} (1-C/n)^{\alpha n^2} \leq e^{-C\alpha n} .\end{equation*}

To see that $D_0 \cup D(n,C/n)$ contains a consistently oriented cycle of length $3$ , we use the second-moment method to show that a.a.s. there exists an edge $\overrightarrow{uv}$ of $D_0$ and a vertex $w \neq u,v$ such that $\overrightarrow{vw}, \overrightarrow{wu}$ are edges of $D(n,C/n)$ . The expected number of such triangles is $\mu \;:\!=\; e(D_0) (n-2) (C/n)^2$ , while the variance is at most

\begin{equation*} \mu \left ( 1 + 2 \cdot 2 (n-3) (C/n) \right ) \leq 5 C \mu,\end{equation*}

since such a triangle intersects $2 \cdot 2 (n-3)$ other such triangles in their random edges — $2$ choices for which edge ( $\overrightarrow{vw}$ or $\overrightarrow{wu}$ ) to intersect, $n-3$ choices for the other vertex $x$ , and $2$ choices for whether $xw$ is the deterministic edge of the other triangle. Since $e(D_0) \geq \alpha n^2$ , $\mu$ is of order $n$ , so by Chebyshev’s inequality, $D_0 \cup D(n,C/n)$ contains a consistently oriented cycle of length $3$ a.a.s.

8. Concluding remarks

In this paper, we have determined how many random edges one must add to a digraph with linear minimum semi-degree to a.a.s. force all orientations of a Hamilton cycle. There has also been interest in obtaining results in the perturbed setting where the initial (di)graph is sparse. In particular, Hahn-Klimroth, Maesaka, Mogge, Mohr, and Parczyk [16] proved a generalisation of the graph version of Theorem 1.1, where now $\alpha$ can be a function of $n$ that tends towards $0$ as $n$ tends to infinity. Let $G(n,p)$ be the binomial random graph on the vertex set $[n]$ where every possible edge is present with probability $p$ , independently of all other edges.

Theorem 8.1 (Hahn-Klimroth, Maesaka, Mogge, Mohr, and Parczyk [16]). Let $\alpha = \alpha (n)\;:\; \mathbb N \rightarrow (0,1)$ and $C =C(\alpha ) = (6+o(1))\log \frac{1}{\alpha }$ . If $G_0$ is an $n$ -vertex graph of minimum degree $\delta (G_0) \geq \alpha n$ , then $G_0 \cup G(n,C/n)$ a.a.s. contains an (undirected) Hamilton cycle.

Note that one cannot take $C=o(\log \frac{1}{\alpha })$ in Theorem 8.1 (see [16, Section 1.1]), so in this sense the theorem is best possible. We can also take $\alpha$ to be non-constant in Theorems 1.3 and 1.4; indeed (taking $\alpha =\eta$ in Theorem 1.4), our proofs give $C = \Theta (\alpha ^{-4})$ and $C = \Theta (\alpha ^{-12})$ respectively. For Theorem 1.3 at least, similarly to Theorem 8.1, we would expect that this could be improved to $C = \Theta (\log \frac{1}{\alpha })$ . It would be interesting to determine the optimal dependence of $C$ on $\alpha$ .

In Theorem 1.4 we studied randomly perturbed digraphs with linear minimum total degree. It is also natural to seek other such total degree results. For example, given any $\alpha \gt 0$ , $k\in \mathbb N$ , $n \in k \mathbb N$ and any $n$ -vertex digraph $D_0$ with $\delta (D_0)\geq \alpha n$ , how many random edges must one add to $D_0$ to ensure that, a.a.s., the resulting digraph contains a $T_k$ -factor? Here by $T_k$ -factor we mean a collection of vertex-disjoint transitive tournaments of size $k$ that together cover $V(D)$ .

Another natural problem is to determine the number of random edges one must add to a digraph with linear minimum semi-degree to a.a.s. force a given oriented spanning tree. The corresponding problem in the graph setting has been studied in [16, 18, 21].

Remark: Since a version of this paper first appeared on arXiv, Morawski and Petrova [26] have resolved this problem for fixed-oriented spanning trees of bounded degree.