Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T14:33:32.580Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal Numbers and the Normality Measure

Published online by Cambridge University Press:  05 April 2013

CHRISTOPH AISTLEITNER
CHRISTOPH AISTLEITNER*
Affiliation:
Department of Applied Mathematics, School of Mathematics and Statistics, University of New South Wales, Sydney NSW 2052, Australia (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In a paper published in this journal, Alon, Kohayakawa, Mauduit, Moreira and Rödl proved that the minimal possible value of the normality measure of an N-element binary sequence satisfies

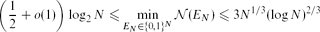\begin{equation*} \biggl( \frac{1}{2} + o(1) \biggr) \log_2 N \leq \min_{E_N \in \{0,1\}^N} \mathcal{N}(E_N) \leq 3 N^{1/3} (\log N)^{2/3} \end{equation*}
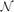for sufficiently large N, and conjectured that the lower bound can be improved to some power of N. In this note it is observed that a construction of Levin of a normal number having small discrepancy gives a construction of a binary sequence EN with (EN) = O((log N)2), thus disproving the conjecture above.

Keywords

Primary 68R15Secondary 11K4511K16
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 3 , May 2013 , pp. 342 - 345
Copyright
Copyright © Cambridge University Press 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aistleitner, C. On the limit distribution of the normality measure of random binary sequences. Preprint. http://arxiv.org/abs/1301.6454.Google Scholar
[2]Alon, N., Kohayakawa, Y., Mauduit, C., Moreira, C. G. and Rödl, V. (2006) Measures of pseudorandomness for finite sequences: Minimal values. Combin. Probab. Comput. 15 1–29.Google Scholar
[3]Alon, N., Kohayakawa, Y., Mauduit, C., Moreira, C. G. and Rödl, V. (2007) Measures of pseudorandomness for finite sequences: Typical values. Proc. Lond. Math. Soc. (3) 95 778–812.Google Scholar
[4]Bailey, D. H. and Crandall, R. E. (2002) Random generators and normal numbers. Experiment. Math. 11 527–546.Google Scholar
[5]Knuth, D. E. (1981) The Art of Computer Programming, Vol. 2, second edition, Addison-Wesley.Google Scholar
[6]Korobov, N. M. (1955) Numbers with bounded quotient and their applications to questions of Diophantine approximation. Izv. Akad. Nauk SSSR Ser. Mat. 19 361–380.Google Scholar
[7]Levin, M. B. (1999) On the discrepancy estimate of normal numbers. Acta Arith. 88 99–111.Google Scholar
[8]Mauduit, C. and Sárközy, A. (1997) On finite pseudorandom binary sequences I: Measure of pseudorandomness, the Legendre symbol. Acta Arith. 82 365–377.Google Scholar
[9]Niederreiter, H. (1992) Random Number Generation and Quasi-Monte Carlo Methods, Vol. 63 of CBMS–NSF Regional Conference Series in Applied Mathematics, SIAM.Google Scholar
[10]Schmidt, W. M. (1972) Irregularities of distribution VII. Acta Arith. 21 45–50.Google Scholar
[11]Wall, D. D. (1949) Normal numbers. PhD thesis, University of California, Berkeley.Google Scholar