Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1995.
Combinatorial Geometry.
p.
319.
Govaerts, P.
Storme, L.
and
Van Maldeghem, H.
2002.
On a Particular Class of Minihypers and its Applications. III. Applications.
European Journal of Combinatorics,
Vol. 23,
Issue. 6,
p.
659.
Pach, János
Radoičić, Radoš
and
Vondrák, Jan
2006.
Nearly equal distances and Szemerédi's regularity lemma.
Computational Geometry,
Vol. 34,
Issue. 1,
p.
11.
Pach, János
Radoičić, Radoš
and
Vondrák, Jan
2006.
On the diameter of separated point sets with many nearly equal distances.
European Journal of Combinatorics,
Vol. 27,
Issue. 8,
p.
1321.
Frankl, Nóra
and
Kupavskii, Andrey
2023.
Nearly k-Distance Sets.
Discrete & Computational Geometry,
Vol. 70,
Issue. 3,
p.
455.
Lichev, Lyuben
and
Mihaylov, Tsvetomir
2024.
Annulus Graphs in $$\mathbb R^d$$.
Discrete & Computational Geometry,
Vol. 72,
Issue. 1,
p.
379.


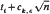 for some 1 ≤
for some 1 ≤ 