Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T02:44:25.112Z Has data issue: false hasContentIssue false
  • English
  • Français

A Multipartite Version of the Hajnal–Szemerédi Theorem for Graphs and Hypergraphs

Published online by Cambridge University Press:  07 December 2012

ALLAN LO  and
KLAS MARKSTRÖM
ALLAN LO
Affiliation:
School of Mathematics, University of Birmingham, Birmingham B15 2TT, UK (e-mail: [email protected])
KLAS MARKSTRÖM
Affiliation:
Department of Mathematics and Mathematical Statistics, Umeå University, S-901 87 Umeå, Sweden (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A perfect Kt-matching in a graph G is a spanning subgraph consisting of vertex-disjoint copies of Kt. A classic theorem of Hajnal and Szemerédi states that if G is a graph of order n with minimum degree δ(G) ≥ (t − 1)n/t and t|n, then G contains a perfect Kt-matching. Let G be a t-partite graph with vertex classes V1, …, Vt each of size n. 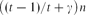We show that, for any γ > 0, if every vertex x ∈ Vi is joined to at least $\bigl ((t-1)/t + \gamma \bigr )n$ vertices of Vj for each j ≠ i, then G contains a perfect Kt-matching, provided n is large enough. Thus, we verify a conjecture of Fischer [6] asymptotically. Furthermore, we consider a generalization to hypergraphs in terms of the codegree.

Keywords

Primary 05C65Secondary 05C7005C07
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 1 , January 2013 , pp. 97 - 111
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aharoni, R., Georgakopoulos, A. and Sprüssel, P. (2009) Perfect matchings in r-partite r-graphs. Europ. J. Combin. 30 39–42.CrossRefGoogle Scholar
[2]Alon, N., Frankl, P., Huang, H., Rödl, V., Ruciński, A. and Sudakov, B. (2012) Large matchings in uniform hypergraphs and the conjectures of Erdős and Samuels. J. Combin. Theory Ser. A 119 1200–1215.Google Scholar
[3]Alon, N. and Spencer, J. H. (2000) The Probabilistic Method, second edition. Wiley–Interscience Series in Discrete Mathematics and Optimization.Google Scholar
[4]Csaba, B. and Mydlarz, M. (2012) Approximate multipartite version of the Hajnal–Szemerédi theorem. J. Combin. Theory Ser. B 102 395–410.Google Scholar
[5]Daykin, D. E. and Häggkvist, R. (1981) Degrees giving independent edges in a hypergraph. Bull. Austral. Math. Soc. 23 103–109.Google Scholar
[6]Fischer, E. (1999) Variants of the Hajnal–Szemerédi theorem. J. Graph Theory 31 275–282.Google Scholar
[7]Frankl, P. and Rödl, V. (1985) Near perfect coverings in graphs and hypergraphs. Europ. J. Combin. 6 317–326.Google Scholar
[8]Hajnal, A. and Szemerédi, E. (1970) Proof of a conjecture of P. Erdős. In Combinatorial Theory and its Applications II: Proc. Colloq., Balatonfüred, 1969, North-Holland, pp. 601–623.Google Scholar
[9]Hàn, H., Person, Y. and Schacht, M. (2009) On perfect matchings in uniform hypergraphs with large minimum vertex degree. SIAM J. Discrete Math. 23 732–748.Google Scholar
[10]Han, J. and Zhao, Y. (2012) On multipartite Hajnal–Szemerédi theorems. arXiv:1203.2667Google Scholar
[11]Johansson, R. (2000) Triangle-factors in a balanced blown-up triangle. Discrete Math. 211 249–254.Google Scholar
[12]Keevash, P. (2011) A hypergraph blow-up lemma. Random Struct. Alg. 39 275–376.Google Scholar
[13]Keevash, P. and Mycroft, R. (2011) A geometric theory for hypergraph matching. arXiv:1108.1757Google Scholar
[14]Keevash, P. and Mycroft, R. (2012) A multipartite Hajnal–Szemerédi theorem. arXiv:1201.1882Google Scholar
[15]Kühn, D. and Osthus, D. (2006) Matchings in hypergraphs of large minimum degree. J. Graph Theory 51 269–280.Google Scholar
[16]Lo, A. and Markström, K. (2011) F-factors in hypergraphs via absorption. arXiv:1105.3411Google Scholar
[17]Lo, A. and Markström, K. (2011) Perfect matchings in 3-partite 3-uniform hypergraphs. arXiv:1103.5654Google Scholar
[18]Lovász, L. and Plummer, M. D. (1986) Matching Theory. Vol. 121 of North-Holland Mathematics Studies, North-Holland.Google Scholar
[19]Magyar, C. and Martin, R. (2002) Tripartite version of the Corrádi–Hajnal theorem. Discrete Math. 254 289–308.Google Scholar
[20]Martin, R. and Szemerédi, E. (2008) Quadripartite version of the Hajnal–Szemerédi theorem. Discrete Math. 308 4337–4360.Google Scholar
[21]Pikhurko, O. (2008) Perfect matchings and K 34-tilings in hypergraphs of large codegree. Graphs Combin. 24 391–404.Google Scholar
[22]Rödl, V., Ruciński, A. and Szemerédi, E. (2009) Perfect matchings in large uniform hypergraphs with large minimum collective degree. J. Combin. Theory Ser. A 116 613–636.Google Scholar