Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T19:50:17.001Z Has data issue: false hasContentIssue false
  • English
  • Français

The Harmonious Chromatic Number of Bounded Degree Trees

Published online by Cambridge University Press:  12 September 2008

Keith Edwards
Keith Edwards
Affiliation:
Department of Mathematics and Computer Science, University of Dundee, Dundee DD1 4HN, UK
Get access Rights & Permissions [Opens in a new window]

Abstract

A harmonious colouring of a simple graph G is a proper vertex colouring such that each pair of colours appears together on at most one edge. The harmonious chromatic number h(G) is the least number of colours in such a colouring. Let d be a fixed positive integer. We show that there is a natural number N(d) such that if T is any tree with m ≥ N(d) edges and maximum degree at most d, then the harmonious chromatic number h(T) is k or k + 1, where k is the least positive integer such that 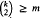. We also give a polynomial time algorithm for determining the harmonious chromatic number of a tree with maximum degree at most d.

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 5 , Issue 1 , March 1996 , pp. 15 - 28
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Edwards, K. J. (1995) The harmonious chromatic number of almost all trees. Combinatorics, Probability and Computing 4 31–46.CrossRefGoogle Scholar
[2]Edwards, K. J. and McDiarmid, C. J. H. (1994) New upper bounds on harmonious colorings. J. Graph Theory. 18 257–267.CrossRefGoogle Scholar
[3]Edwards, K. J. and McDiarmid, C.J. H. (1995) The complexity of harmonious colouring for trees. Disc. Appl. Maths 57 133–144.Google Scholar
[4]Fiorini, S. and Wilson, R. J. (1977) Edge-colourings of graphs. Pitman Research Notes in Mathematics 16, Pitman, London.Google Scholar
[5]Frank, O., Harary, F. and Plantholt, M. (1982) The line-distinguishing chromatic number of a graph. Ars Combinatoria 14 241–252.Google Scholar
[6]Hopcroft, J. and Krishnamoorthy, M. S. (1983) On the harmonious coloring of graphs. SIAM J. Alg. Disc. Methods 4 306–311.CrossRefGoogle Scholar
[7]König, D. (1916) Über Graphen und ihre Anwendung auf Determinantentheorie und Mengenlehre. Math. Ann. 77 453–465.Google Scholar
[8]Krasikov, I. and Roditty, Y. (1994) Bounds for the harmonious chromatic number of a graph. J. Graph Theory 18 205–209.Google Scholar
[9]Miller, Z. and Pritikin, D. (1991) The harmonious colouring number of a graph. Disc. Maths. 93 211–228.Google Scholar
[10]Mitchem, J. (1989) On the harmonious chromatic number of a graph. Disc. Maths. 74 151–157.Google Scholar
[11]Wilson, B. (1990) Line distinguishing and harmonious colourings. In: Nelson, R. and Wilson, R. J. (eds.) Graph Colourings: Pitman Research Notes in Mathematics 218 115–133, Longman Scientific & Technical.Google Scholar