Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T08:45:38.355Z Has data issue: false hasContentIssue false
  • English
  • Français

Full rainbow matchings in graphs and hypergraphs

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  20 January 2021

Pu Gao ,
Reshma Ramadurai ,
Ian M. Wanless  and
Nick Wormald
Pu Gao
Affiliation:
Department of Combinatorics and Optimization, University of Waterloo, Ontario, N2L 3G1, Canada
Reshma Ramadurai
Affiliation:
School of Mathematics & Statistics, Victoria University of Wellington, Wellington6140, New Zealand
Ian M. Wanless
Affiliation:
School of Mathematics, Monash University, Victoria3800, Australia
Nick Wormald*
Affiliation:
School of Mathematics, Monash University, Victoria3800, Australia
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a simple graph that is properly edge-coloured with m colours and let 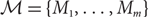\[\mathcal{M} = \{ {M_1},...,{M_m}\} \] be the set of m matchings induced by the colours in G. Suppose that 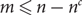\[m \leqslant n - {n^c}\], where 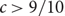\[c > 9/10\], and every matching in 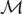\[\mathcal{M}\] has size n. Then G contains a full rainbow matching, i.e. a matching that contains exactly one edge from Mi for each 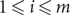\[1 \leqslant i \leqslant m\]. This answers an open problem of Pokrovskiy and gives an affirmative answer to a generalization of a special case of a conjecture of Aharoni and Berger. Related results are also found for multigraphs with edges of bounded multiplicity, and for hypergraphs.

Finally, we provide counterexamples to several conjectures on full rainbow matchings made by Aharoni and Berger.

MSC classification

Primary: 05D15: Transversal (matching) theory
Secondary: 05C70: Factorization, matching, partitioning, covering and packing
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 5 , September 2021 , pp. 762 - 780
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported by the ARC grant DE170100716. The research was conducted when the author was affiliated with Monash University.

‡

Research supported by the ARC grant DP150100506.

§

Research supported by the Australian Laureate Fellowships grant FL120100125.

References

Aharoni, R. and Berger, E. (2009) Rainbow matchings in r-partite r-graphs. Electron. J. Combin. 16 #R119.CrossRefGoogle Scholar
Aharoni, R., Berger, E., Chudnovsky, M., Howard, D. and Seymour, P. (2016) Large rainbow matchings in general graphs. arXiv:1611.03648v3Google Scholar
Aharoni, R., Berger, E., Chudnovsky, M., Howard, D. and Seymour, P. (2019) Large rainbow matchings in general graphs. European J. Combin. 79 222–227.CrossRefGoogle Scholar
Aharoni, R., Charbit, P. and Howard, D. (2015) On a generalization of the Ryser–Brualdi–Stein conjecture. J. Graph Theory 78 143–156.10.1002/jgt.21796CrossRefGoogle Scholar
Aharoni, R., Kotlar, D. and Ziv, R. (2017) Representation of large matchings in bipartite graphs. SIAM J. Discrete Math. 31 1726–1731.CrossRefGoogle Scholar
Alon, N. (1992) The strong chromatic number of a graph. Random Struct. Algorithms 3 1–7.CrossRefGoogle Scholar
Alon, N. and Spencer, J. (2000) The Probabilistic Method, Wiley.10.1002/0471722154CrossRefGoogle Scholar
Azuma, K. (1967) Weighted sums of certain dependent random variables. Tohoku Math. J. (Second Series) 19 357–367.CrossRefGoogle Scholar
Barát, J., Gyárfás, A. and Sárközy, G. N. (2017) Rainbow matchings in bipartite multigraphs. Period. Math. Hungar. 74 108–111.CrossRefGoogle Scholar
Barát, J. and Wanless, I. M. (2014) Rainbow matchings and transversals. Australas. J. Combin. 59 211–217.Google Scholar
Best, D., Hendrey, K., Wanless, I. M., Wilson, T. E. and Wood, D. R. (2018) Transversals in Latin arrays with many distinct symbols. J. Combin. Des. 26 84–96.CrossRefGoogle Scholar
Cavenagh, N. J. and Wanless, I. M. (2017) Latin squares with no transversals. Electron. J. Combin. 24 #P2.45.CrossRefGoogle Scholar
Clemens, D. and Ehrenmüller, J. (2016) An improved bound on the sizes of matchings guaranteeing a rainbow matching. Electron. J. Combin. 23 #P2.11.CrossRefGoogle Scholar
Dubhashi, D. P. and Panconesi, A. (2009) Concentration of Measure for the Analysis of Randomized Algorithms, Cambridge University Press.CrossRefGoogle Scholar
Gao, P., Ramadurai, R., Wanless, I. M. and Wormald, N. (2017) Counterexamples on matchings in hypergraphs and full rainbow matchings in graphs. arXiv:1710.04807Google Scholar
Häggkvist, R. and Johansson, A. (2008) Orthogonal Latin rectangles. Combin. Probab. Comput. 17 519–536.CrossRefGoogle Scholar
Hatami, P. and Shor, P. W. (2008) A lower bound for the length of a partial transversal in a Latin square. J. Combin. Theory Ser. A 115 1103–1113.CrossRefGoogle Scholar
Hoeffding, W. (1963) Probability inequalities for sums of bounded random variables. J. Amer. Statist. Assoc. 58 (301) 13–30.CrossRefGoogle Scholar
Jin, G. (1992) Complete subgraphs of r-partite graphs. Combin. Probab. Comput. 1 241–250.CrossRefGoogle Scholar
Keevash, P. and Yepremyan, L. (2018) Rainbow matchings in properly colored multigraphs. SIAM J. Discrete Math. 32 1577–1584.CrossRefGoogle Scholar
Keevash, P. and Yepremyan, L. (2020) On the number of symbols that forces a transversal. Combin. Probab. Comput. 29 234–240.CrossRefGoogle Scholar
Kotlar, D. and Ziv, R. (2014) Large matchings in bipartite graphs have a rainbow matching. European J. Combin. 38 97–101.CrossRefGoogle Scholar
McDiarmid, C. (2002) Concentration for independent permutations. Combin. Probab. Comput. 11 163–178.CrossRefGoogle Scholar
Montgomery, R., Pokrovskiy, A. and Sudakov, B. (2019) Decompositions into spanning rainbow structures. Proc. Lond. Math. Soc. (3) 119 899–959.CrossRefGoogle Scholar
Pokrovskiy, A. (2017) Rainbow matchings and rainbow connectedness. Electron. J. Combin. 24 #P1.13.CrossRefGoogle Scholar
Pokrovskiy, A. (2018) An approximate version of a conjecture of Aharoni and Berger. Adv. Math. 333 1197–1241.CrossRefGoogle Scholar
Ryser, H. (1967) Neuere Probleme der Kombinatorik. In Vorträge über Kombinatorik, Oberwolfach, pp. 69–91.Google Scholar
Stein, S. K. (1975) Transversals of Latin squares and their generalizations. Pacific J. Math. 59 567–575.CrossRefGoogle Scholar
Wanless, I. M. (2011) Transversals in Latin squares: a survey. In Surveys in Combinatorics 2011 (Chapman, R., ed.), Vol. 392 of London Mathematical Society Lecture Note Series, pp. 403–437. Cambridge University Press.CrossRefGoogle Scholar