Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T09:35:49.163Z Has data issue: false hasContentIssue false
  • English
  • Français

First Occurrence in Pairs of Long Words: A Penney-ante Conjecture of Pevzner

Published online by Cambridge University Press:  12 September 2008

Dudley Stark
Dudley Stark
Affiliation:
Institut für Angewandte Mathematik, Universität Zürich, Winterthurerstr. 190, CH-8057 Zurich, Switzerland
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose X1, X2,… is a sequence of independent and identically distributed random elements whose values are taken in a finite set S of size |S| ≥ 2 with probability distribution ℙ(X = s) = p(s) > 0 for s ∈ S. Pevzner has conjectured that for every probability distribution ℙ there exists an N > 0 such that for every word A with letters in S whose length is at least N, there exists a second word B of the same length as A, such that the event that B appears before A in the sequence X1, X2,… has greater probability than that of A appearing before B. In this paper it is shown that a distribution ℙ satisfies Pevzner's conclusion if and only if the maximum value of ℙ, p, and the secondary maximum c satisfy the inequality 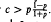. For |S| = 2 or |S| = 3, the inequality is true and the conjecture holds. If 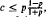, then the conjecture is true when A is not allowed to consist of pure repetitions of that unique element for which the distribution takes on its mode.

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 4 , Issue 3 , September 1995 , pp. 279 - 285
Copyright
Copyright © Cambridge University Press 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Breen, S., Waterman, M.S. and Zhang, N. (1985) Renewal Theory for Several Patterns. J. Appl. Prob. 22 228–234.CrossRefGoogle Scholar
[2]Chen, R. (1989) A Circular Property of the Occurrence of Sequence Patterns in the Fair Coin-Tossing Process. Adv. Appl. Prob. 21 938–940.CrossRefGoogle Scholar
[3]Guibas, L. J. and Odlyzko, A.M. (1981) Periods in Strings. J. Comb. Theory A 30 19–42.CrossRefGoogle Scholar
[4]Guibas, L. J. and Odlyzko, A.M. (1981) String Overlaps, Pattern Matching and Nontransitive Games, J. Comb. Theory A 30 183–208.CrossRefGoogle Scholar
[5]Li, S.-Y. R. (1980) A Martingale Approach to the Study of Occurrence of Sequence Patterns in Repeated Experiments. Annal. Prob. 8 1171–1176.Google Scholar
[6]Penney, W. (1969) Problem: Penney-ante. J. Rec. Math. 2 241.Google Scholar
[7]Pevzner, P. (1987) The Best Bet for Simpletons. Kvantl 5 4–15.Google Scholar