Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T11:45:58.510Z Has data issue: false hasContentIssue false
  • English
  • Français

Deterministic counting of graph colourings using sequences of subgraphs

Part of: Discrete mathematics in relation to computer science Algorithms - Computer Science Equilibrium statistical mechanics

Published online by Cambridge University Press:  22 June 2020

Charilaos Efthymiou
Charilaos Efthymiou*
Affiliation:
Department of Computer Science, University of Warwick, CoventryCV4 7AL, UK
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we propose a polynomial-time deterministic algorithm for approximately counting the k-colourings of the random graph G(n, d/n), for constant d>0. In particular, our algorithm computes in polynomial time a 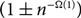$(1\pm n^{-\Omega(1)})$ -approximation of the so-called ‘free energy’ of the k-colourings of G(n, d/n), for 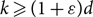$k\geq (1+\varepsilon) d$ with probability 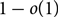$1-o(1)$ over the graph instances.

Our algorithm uses spatial correlation decay to compute numerically estimates of marginals of the Gibbs distribution. Spatial correlation decay has been used in different counting schemes for deterministic counting. So far algorithms have exploited a certain kind of set-to-point correlation decay, e.g. the so-called Gibbs uniqueness. Here we deviate from this setting and exploit a point-to-point correlation decay. The spatial mixing requirement is that for a pair of vertices the correlation between their corresponding configurations becomes weaker with their distance.

Furthermore, our approach generalizes in that it allows us to compute the Gibbs marginals for small sets of nearby vertices. Also, we establish a connection between the fluctuations of the number of colourings of G(n, d/n) and the fluctuations of the number of short cycles and edges in the graph.

MSC classification

Primary: 68R99: None of the above, but in this section
Secondary: 68W25: Approximation algorithms 68W20: Randomized algorithms 82B44: Disordered systems (random Ising models, random Schrödinger operators, etc.)
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 4 , July 2020 , pp. 555 - 586
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported by Centre of Discrete Mathematics and Applications (DIMAP), University of Warwick, EPSRC award, and DFG grant EF 103/1-1.

References

Achlioptas, D. and Coja-Oghlan, A. (2008) Algorithmic barriers from phase transitions. In 49th Annual IEEE Symposium on Foundations of Computer Science (FOCS), pp. 793–802.Google Scholar
Aldous, D. (1983) Random walks of finite groups and rapidly mixing Markov chains. In Séminaire de Probabilités XVII 1981/82, Springer, pp. 243–297.CrossRefGoogle Scholar
Bandyopadhyay, A. and Gamarnik, D. (2008) Counting without sampling: new algorithms for enumeration problems using statistical physics. Random Struct. Algorithms 33 452–479.CrossRefGoogle Scholar
Bapst, V., Coja-Oghlan, A. and Efthymiou, C. (2017) Planting colourings silently. Combin. Probab. Comput. 26 338–366.CrossRefGoogle Scholar
Bapst, V., Coja-Oghlan, A., Hetterich, S., Rassmann, F. and Vilenchik, D. (2017) The condensation phase transition in random graph coloring. Commun. Math. Phys. 341 543–606.CrossRefGoogle Scholar
Coja-Oghlan, A., Efthymiou, C. and Jaafari, N. (2018) Local convergence of random graph colorings. Combinatorica 38 341–380.Google Scholar
Efthymiou, C. (2015) Reconstruction/non-reconstruction thresholds for colourings of general Galton–Watson trees. In Approximation, Randomization, and Combinatorial Optimization: Algorithms and Techniques (APPROX–RANDOM), pp. 756–774.Google Scholar
Efthymiou, C. (2016) A simple algorithm for sampling colorings of G(n,d/n) up to the Gibbs uniqueness threshold. SIAM J. Comput. 45 2087–2116.Google Scholar
Efthymiou, C., Hayes, T., Štefankovič, D. and Vigoda, E. (2018) Sampling random colorings of sparse random graphs. In 29th Annual ACM–SIAM Symposium on Discrete Algorithms (SODA ’18), pp. 1759–1771.Google Scholar
Janson, S. (1995) Random regular graphs: asymptotic distributions and contiguity. Combin. Probab. Comput. 4 369–405.Google Scholar
Jerrum, M. and Sinclair, A. (1986) Approximate counting, uniform generation and rapidly mixing Markov chains. Inform. Comput. 82 93–133.Google Scholar
Jerrum, M. and Sinclair, A. (1996) The Markov chain Monte Carlo method: an approach to approximate counting and integration. In Approximation Algorithms for NP-hard problems (Hochbaum, D. S., ed.), PWS.Google Scholar
Jerrum, M., Valiant, L. G. and Vazirani, V. V. (1986) Random generation of combinatorial structures from a uniform distribution. Theoret. Comput. Sci. 43 169–188.CrossRefGoogle Scholar
Krzakala, F., Montanari, A., Ricci-Tersenghi, F., Semerjianc, G. and Zdeborova, L. (2007) Gibbs states and the set of solutions of random constraint satisfaction problems. Proc. Nat. Acad. Sci. 104 10318–10323.Google Scholar
Mézard, M. and Montanari, A. (2009) Information, Physics and Computation, Oxford University Press.CrossRefGoogle Scholar
Mézard, M., Parisi, G. and Zecchina, R. (2002) Analytic and algorithmic solution of random satisfiability problems. Science 297 812–815.Google ScholarPubMed
Montanari, A. and Shah, D. (2007) Counting good truth assignments of random k-SAT formulae. In 18th Annual ACM–SIAM Symposium on Discrete Algorithms (SODA ’07), pp. 1255–1264.Google Scholar
Mossel, E. and Sly, A. (2009) Rapid mixing of Gibbs sampling on graphs that are sparse on average. Random Struct. Algorithms 35 250–270.CrossRefGoogle Scholar
Restrepo, R., Shin, J., Tetali, P., Vigoda, E. and Yang, L. (2013) Improved mixing condition on the grid for counting and sampling independent sets. Probab. Theory Related Fields 156 75–99.CrossRefGoogle Scholar
Robinson, R. and Wormald, N. (1994) Almost all regular graphs are Hamiltonian. Random Struct. Algorithms 5 363–374.Google Scholar
Sinclair, A., Srivastava, P. and Thurley, M. (2014) Approximation algorithms for two-state anti-ferromagnetic spin systems on bounded degree graphs. J. Statist. Phys. 155 666–686.CrossRefGoogle Scholar
Sinclair, A., Srivastava, P. and Yin, Y. (2013) Spatial mixing and approximation algorithms for graphs with bounded connective constant. In 54th Annual IEEE Symposium on Foundations of Computer Science (FOCS), pp. 300–309.CrossRefGoogle Scholar
Vigoda, E. (2000) Improved bounds for sampling colorings. J. Math. Phys. 41 1555–1569.CrossRefGoogle Scholar
Wainright, M. J. and Jordan, M. (2008) Graphical models, exponential families and variational inference. In Found. Trends Mach. Learn. 1 (1–2).Google Scholar
Weitz, D. (2006) Counting independent sets up to the tree threshold. In 38th Annual ACM Symposium of Theory of Computing (STOC ’06), pp. 140–149.CrossRefGoogle Scholar
Yin, Y. and Zhang, C. (2016) Sampling in Potts model on sparse random graphs. In Approximation, Randomization, and Combinatorial Optimization: Algorithms and Techniques (APPROX–RANDOM), pp. 1–22.Google Scholar