Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T19:01:29.348Z Has data issue: false hasContentIssue false
  • English
  • Français

Detachments of Hypergraphs I: The Berge–Johnson Problem

Published online by Cambridge University Press:  27 February 2012

M. A. BAHMANIAN
M. A. BAHMANIAN*
Affiliation:
Department of Mathematics and Statistics, Auburn University, Auburn, AL 36849-5310, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A detachment of a hypergraph is formed by splitting each vertex into one or more subvertices, and sharing the incident edges arbitrarily among the subvertices. For a given edge-coloured hypergraph 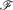, we prove that there exists a detachment 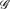such that the degree of each vertex and the multiplicity of each edge in 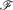(and each colour class of 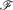) are shared fairly among the subvertices in 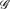(and each colour class of 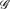, respectively).

Let 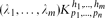be a hypergraph with vertex partition {V1,. . .,Vn}, |Vi| = pi for 1 ≤ i ≤ n such that there are λi edges of size hi incident with every hi vertices, at most one vertex from each part for 1 ≤ i ≤ m (so no edge is incident with more than one vertex of a part). We use our detachment theorem to show that the obvious necessary conditions for 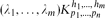to be expressed as the union 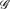1 ∪ ··· ∪ 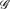k of k edge-disjoint factors, where for 1 ≤ i ≤ k, 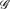i is ri-regular, are also sufficient. Baranyai solved the case of h1 = ··· = hm, λ1 = ··· = λm = 1, p1 = ··· = pm, r1 = ··· = rk. Berge and Johnson (and later Brouwer and Tijdeman, respectively) considered (and solved, respectively) the case of hi = i, 1 ≤ i ≤ m, p1 = ··· = pm = λ1 = ··· = λm = r1 = ··· = rk = 1. We also extend our result to the case where each 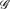i is almost regular.

Keywords

05C6505C1505C7005C5105B4005B05
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 4 , July 2012 , pp. 483 - 495
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bahmanian, M. A. and Rodger, C. A.Multiply balanced edge colorings of multigraphs. J. Graph Theory. doi:10.1002/jgt.20617.Google Scholar
[2]Baranyai, Z. (1975) On the factorization of the complete uniform hypergraph. In Infinite and Finite Sets I: Colloq., Keszthely, 1973, dedicated to P. Erdős on his 60th birthday, Vol. of Colloq. Math. Soc. Janos Bolyai, North-Holland, pp. 91–108.Google Scholar
[3]Baranyai, Z. (1979) The edge-coloring of complete hypergraphs I. J. Combin. Theory Ser. B 26 276–294.CrossRefGoogle Scholar
[4]Berge, C. and Johnson, E. L. (1977) Coloring the edges of a hypergraph and linear programming techniques. In Studies in Integer Programming: Proc. Workshop, Bonn, 1975. Ann. Discrete Math. 1 65–78.CrossRefGoogle Scholar
[5]Brouwer, A. E. (1977) On the edge-colouring property for the hereditary closure of a complete uniform hypergraph. Mathematisch Centrum, Amsterdam, Afdeling Zuivere Wiskunde. No. ZW 95/77.Google Scholar
[6]Brouwer, A. E. and Tijdeman, R. (1981) On the edge-colouring problem for unions of complete uniform hypergraphs. Discrete Math. 34 241–260.CrossRefGoogle Scholar
[7]Ferencak, M. N. and Hilton, A. J. W. (2002) Outline and amalgamated triple systems of even index. Proc. London Math. Soc. (3) 84 1–34.CrossRefGoogle Scholar
[8]Hilton, A. J. W. (1980) The reconstruction of Latin squares with applications to school timetabling and to experimental design. Math. Programming Study 13 68–77.CrossRefGoogle Scholar
[9]Hilton, A. J. W. (1984) Hamiltonian decompositions of complete graphs. J. Combin. Theory Ser. B 36 125–134.CrossRefGoogle Scholar
[10]Hilton, A. J. W. (1987) Outlines of Latin squares. In Combinatorial Design Theory, Vol.149 of North-Holland Math. Stud., North-Holland, pp. 225–241.CrossRefGoogle Scholar
[11]Hilton, A. J. W., Johnson, M., Rodger, C. A. and Wantland, E. B. (2003) Amalgamations of connected k-factorizations. J. Combin. Theory Ser. B 88 267–279.CrossRefGoogle Scholar
[12]Hilton, A. J. W. and Rodger, C. A. (1986) Hamiltonian decompositions of complete regular s-partite graphs. Discrete Math. 58 63–78.CrossRefGoogle Scholar
[13]Johnson, E. L. (1978) On the edge-coloring property for the closure of the complete hypergraphs. In Algorithmic Aspects of Combinatorics: Conf., Vancouver Island, BC, 1976. Ann. Discrete Math. 2 161–171.CrossRefGoogle Scholar
[14]Johnson, M. (2007) Amalgamations of factorizations of complete graphs. J. Combin. Theory Ser. B 97 597–611.CrossRefGoogle Scholar
[15]Leach, C. D. and Rodger, C. A. (2001) Non-disconnecting disentanglements of amalgamated 2-factorizations of complete multipartite graphs. J. Combin. Designs 9 460–467.CrossRefGoogle Scholar
[16]Leach, C. D. and Rodger, C. A. (2003) Hamilton decompositions of complete multipartite graphs with any 2-factor leave. J. Graph Theory 44 208–214.CrossRefGoogle Scholar
[17]Leach, C. D. and Rodger, C. A. (2004) Hamilton decompositions of complete graphs with a 3-factor leave. Discrete Math. 279 337–344.CrossRefGoogle Scholar
[18]Nash-Williams, C. St. J. A. (1987) Amalgamations of almost regular edge-colourings of simple graphs. J. Combin. Theory Ser. B 43 322–342.CrossRefGoogle Scholar
[19]Rodger, C. A. and Wantland, E. B. (1995) Embedding edge-colorings into 2-edge-connected k-factorizations of K kn + 1. J. Graph Theory 19 169–185.CrossRefGoogle Scholar