Article contents
Degree Ramsey Numbers of Graphs
Published online by Cambridge University Press: 02 February 2012
Abstract
Let H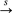 G mean that every s-colouring of E(H) produces a monochromatic copy of G in some colour class. Let the s-colour degree Ramsey number of a graph G, written RΔ(G; s), be min{Δ(H): H
G mean that every s-colouring of E(H) produces a monochromatic copy of G in some colour class. Let the s-colour degree Ramsey number of a graph G, written RΔ(G; s), be min{Δ(H): H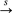 G}. If T is a tree in which one vertex has degree at most k and all others have degree at most ⌈k/2⌉, then RΔ(T; s) = s(k − 1) + ϵ, where ϵ = 1 when k is odd and ϵ = 0 when k is even. For general trees, RΔ(T; s) ≤ 2s(Δ(T) − 1).
G}. If T is a tree in which one vertex has degree at most k and all others have degree at most ⌈k/2⌉, then RΔ(T; s) = s(k − 1) + ϵ, where ϵ = 1 when k is odd and ϵ = 0 when k is even. For general trees, RΔ(T; s) ≤ 2s(Δ(T) − 1).
To study sharpness of the upper bound, consider the double-starSa,b, the tree whose two non-leaf vertices have degrees a and b. If a ≤ b, then RΔ(Sa,b; 2) is 2b − 2 when a < b and b is even; it is 2b − 1 otherwise. If s is fixed and at least 3, then RΔ(Sb,b;s) = f(s)(b − 1) − o(b), where f(s) = 2s − 3.5 − O(s−1).
We prove several results about edge-colourings of bounded-degree graphs that are related to degree Ramsey numbers of paths. Finally, for cycles we show that RΔ(C2k + 1; s) ≥ 2s + 1, that RΔ(C2k; s) ≥ 2s, and that RΔ(C4;2) = 5. For the latter we prove the stronger statement that every graph with maximum degree at most 4 has a 2-edge-colouring such that the subgraph in each colour class has girth at least 5.
- Type
- Paper
- Information
- Combinatorics, Probability and Computing , Volume 21 , Issue 1-2: Honouring the Memory of Richard H. Schelp , March 2012 , pp. 229 - 253
- Copyright
- Copyright © Cambridge University Press 2012
References
- 8
- Cited by


