Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T18:02:12.379Z Has data issue: false hasContentIssue false
  • English
  • Français

Correlation Bounds for Distant Parts of Factor of IID Processes

Published online by Cambridge University Press:  01 August 2017

ÁGNES BACKHAUSZ ,
BALÁZS GERENCSÉR ,
VIKTOR HARANGI  and
MÁTÉ VIZER
ÁGNES BACKHAUSZ
Affiliation:
Department of Probability and Statistics, Eötvös Loránd University, Pázmány Péter sétány 1/c, H-1117 Budapest, Hungary (e-mail: [email protected]) MTA Alfréd Rényi Institute of Mathematics, Reáltanoda utca 13-15, H-1053 Budapest, Hungary (e-mail: [email protected], [email protected], [email protected])
BALÁZS GERENCSÉR
Affiliation:
Department of Probability and Statistics, Eötvös Loránd University, Pázmány Péter sétány 1/c, H-1117 Budapest, Hungary (e-mail: [email protected]) MTA Alfréd Rényi Institute of Mathematics, Reáltanoda utca 13-15, H-1053 Budapest, Hungary (e-mail: [email protected], [email protected], [email protected])
VIKTOR HARANGI
Affiliation:
MTA Alfréd Rényi Institute of Mathematics, Reáltanoda utca 13-15, H-1053 Budapest, Hungary (e-mail: [email protected], [email protected], [email protected])
MÁTÉ VIZER
Affiliation:
MTA Alfréd Rényi Institute of Mathematics, Reáltanoda utca 13-15, H-1053 Budapest, Hungary (e-mail: [email protected], [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study factor of i.i.d. processes on the d-regular tree for d ≥ 3. We show that if such a process is restricted to two distant connected subgraphs of the tree, then the two parts are basically uncorrelated. More precisely, any functions of the two parts have correlation at most 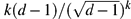$k(d-1) / (\sqrt{d-1})^k$, where k denotes the distance between the subgraphs. This result can be considered as a quantitative version of the fact that factor of i.i.d. processes have trivial 1-ended tails.

Keywords

Primary 60K35Secondary 37A50
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 27 , Issue 1 , January 2018 , pp. 1 - 20
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Alon, N., Benjamini, I., Lubetzky, E. and Sodin, S. (2007) Non-backtracking random walks mix faster. Commun. Contemp. Math. 9 585–603.Google Scholar
[2] Angel, O., Friedman, J. and Hoory, S. (2015) The non-backtracking spectrum of the universal cover of a graph. Trans. Amer. Math. Soc. 367 4287–4318.Google Scholar
[3] Backhausz, Á. and Szegedy, B. (2014) On large girth regular graphs and random processes on trees. arXiv:1406.4420 Google Scholar
[4] Backhausz, Á. and Virág, B. (2015) Spectral measures of factor of i.i.d. processes on vertex-transitive graphs. Ann. Inst. Henri Poincaré Probab. Stat., to appear. arXiv:1505.07412 Google Scholar
[5] Backhausz, Á., Szegedy, B. and Virág, B. (2015) Ramanujan graphings and correlation decay in local algorithms. Random Struct. Alg. 47 424–435.CrossRefGoogle Scholar
[6] Ball, K. (2005) Factors of independent and identically distributed processes with non-amenable group actions. Ergodic Theory Dyn. Syst. 25 711–730.Google Scholar
[7] Ben-Hamou, A. and Salez, J. (2017) Cutoff for non-backtracking random walks on sparse random graphs. Ann. Probab., 45, no. 3, 1752–1770.CrossRefGoogle Scholar
[8] Bordenave, C. (2015) A new proof of Friedman's second eigenvalue theorem and its extension to random lifts. arXiv:1502.04482 Google Scholar
[9] Bowen, L. (2010) The ergodic theory of free group actions: Entropy and the f-invariant. Groups Geom. Dyn. 4 419–432.CrossRefGoogle Scholar
[10] Bowen, L. (2012) Sofic entropy and amenable groups. Ergodic Theory Dynam. Systems 32 427–466.CrossRefGoogle Scholar
[11] Conley, C. T., Marks, A. S. and Tucker-Drob, R. (2016) Brooks's theorem for measurable colorings. Forum of Mathematics, Sigma, 4 e16. DOI: https://doi.org/10.1017/fms.2016.14.CrossRefGoogle Scholar
[12] Csóka, E. (2016) Independent sets and cuts in large-girth regular graphs. arXiv:1602.02747 Google Scholar
[13] Csóka, E. and Lippner, G. (2017) Invariant random matchings in Cayley graphs. Groups, Geometry and Dynamics, 11 211–243.Google Scholar
[14] Csóka, E., Gerencsér, B., Harangi, V. and Virág, B. (2015) Invariant Gaussian processes and independent sets on regular graphs of large girth. Random Struct. Alg. 47 284–303.Google Scholar
[15] Friedman, J. (2008) A Proof of Alon's Second Eigenvalue Conjecture and Related Problems, Vol. 195, no. 910 of Memoirs of the American Mathematical Society, AMS.Google Scholar
[16] Gaboriau, D. and Lyons, R. (2009) A measurable-group-theoretic solution to von Neumann's problem. Invent. Math. 177 533–540.Google Scholar
[17] Gamarnik, D. and Sudan, M. (2014) Limits of local algorithms over sparse random graphs. In ITCS 2014: Proc. 5th Conference on Innovations in Theoretical Computer Science, ACM, pp. 369–376.Google Scholar
[18] Harangi, V. and Virág, B. (2015) Independence ratio and random eigenvectors in transitive graphs. Ann. Probab. 43 2810–2840.Google Scholar
[19] Hoppen, C. and Wormald, N. Local algorithms, regular graphs of large girth, and random regular graphs. Combinatorica, to appear. arXiv:1308.0266 Google Scholar
[20] Kechris, A. S. and Tsankov, T. (2008) Amenable actions and almost invariant sets. Proc. Amer. Math. Soc. 136 687–697.Google Scholar
[21] Kempton, M. (2016) Non-backtracking random walks and a weighted Ihara's theorem. Open J. Discrete Math. 6 207–226.Google Scholar
[22] Kerr, D. and Li, H. (2013) Soficity, amenability, and dynamical entropy. Amer. J. Math. 135 721–761.CrossRefGoogle Scholar
[23] Kun, G. (2013) Expanders have a spanning Lipschitz subgraph with large girth. arXiv:1303.4982 Google Scholar
[24] Lyons, R. (2017) Factors of IID on trees. Combin. Probab. Comput. 26 285–300.CrossRefGoogle Scholar
[25] Lyons, R. and Nazarov, F. (2011) Perfect matchings as IID factors on non-amenable groups. European J. Combin. 32 1115–1125.Google Scholar
[26] Ornstein, D. S. and Weiss, B. (1987) Entropy and isomorphism theorems for actions of amenable groups. J. Analyse Math. 48 1–141.Google Scholar
[27] Pemantle, R. (1992) Automorphism invariant measures on trees. Ann. Probab. 20 1549–1566.Google Scholar
[28] Puder, D. (2015) Expansion of random graphs: New proofs, new results. Invent. Math. 201 845–908.Google Scholar
[29] Rahman, M. (2016) Factor of iid percolation on trees. SIAM J. Discrete Math. 30 2217–2242.CrossRefGoogle Scholar
[30] Rahman, M. and Virág, B. (2017) Local algorithms for independent sets are half-optimal. Ann. Probab., 45, no. 3, 1543–1577.Google Scholar
[31] Rokhlin, V. A. and Sinai, Y. G. (1961) Construction and properties of invariant measurable divisions. Doklady Akademii Nauk SSSR 141 1038–1041.Google Scholar
[32] Seward, B. (2016) Weak containment and Rokhlin entropy. arXiv:1602.06680 Google Scholar