Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T18:42:55.002Z Has data issue: false hasContentIssue false
  • English
  • Français

Cops and Robbers on Geometric Graphs

Published online by Cambridge University Press:  16 August 2012

ANDREW BEVERIDGE ,
ANDRZEJ DUDEK ,
ALAN FRIEZE  and
TOBIAS MÜLLER
ANDREW BEVERIDGE
Affiliation:
Department of Mathematics, Statistics and Computer Science, Macalester College, Saint Paul, MN 55015, USA (e-mail: [email protected])
ANDRZEJ DUDEK
Affiliation:
Department of Mathematics, Western Michigan University, Kalamazoo, MI 49008, USA (e-mail: [email protected])
ALAN FRIEZE
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213, USA (e-mail: [email protected])
TOBIAS MÜLLER
Affiliation:
Centrum voor Wiskunde en Informatica, 1098 XG Amsterdam, the Netherlands (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Cops and robbers is a turn-based pursuit game played on a graph G. One robber is pursued by a set of cops. In each round, these agents move between vertices along the edges of the graph. The cop number c(G) denotes the minimum number of cops required to catch the robber in finite time. We study the cop number of geometric graphs. For points x1, . . ., xn ∈ ℝ2, and r ∈ ℝ+, the vertex set of the geometric graph G(x1, . . ., xn; r) is the graph on these n points, with xi, xj adjacent when ∥xi − xj∥ ≤ r. We prove that c(G) ≤ 9 for any connected geometric graph G in ℝ2 and we give an example of a connected geometric graph with c(G) = 3. We improve on our upper bound for random geometric graphs that are sufficiently dense. Let 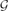(n,r) denote the probability space of geometric graphs with n vertices chosen uniformly and independently from [0,1]2. For G ∈ 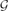(n,r), we show that with high probability (w.h.p.), if r ≥ K1 (log n/n)1/4 then c(G) ≤ 2, and if r ≥ K2(log n/n)1/5 then c(G) = 1, where K1, K2 > 0 are absolute constants. Finally, we provide a lower bound near the connectivity regime of 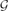(n,r): if r ≤ K3 log n/ 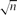then c(G) > 1 w.h.p., where K3 > 0 is an absolute constant.

Keywords

Primary 05C57Secondary 60D0505C80
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 6 , November 2012 , pp. 816 - 834
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aigner, M. and Fromme, M. (1983) A game of cops and robbers. Discrete Appl. Math. 8 1–12.Google Scholar
[2]Alon, N. (2011) Personal communication.Google Scholar
[3]Alspach, B. (2006) Sweeping and searching in graphs: A brief survey. Mathematiche 59 5–37.Google Scholar
[4]Avin, C. and Ercal, G. (2007) On the cover time and mixing time of random geometric graphs Theor. Comput. Sci. 380 2–22.Google Scholar
[5]Baird, W. and Bonato, A. Meyniel's conjecture on the cop number: A survey. Submitted.Google Scholar
[6]Bhadauria, D. and Isler, V. (2011) Capturing an evader in a polygonal environment with obstacles. In Proc. Twenty-Second International Joint Conference on Artificial Intelligence, Vol. 3, AAAI Press, pp. 2054–2059.Google Scholar
[7]Bollobás, B., Kun, G. and Leader, I. Cops and robbers in random graphs. Submitted.Google Scholar
[8]Bonato, A., Kemkes, G. and Prałat, P. (2012) Almost all cop-win graphs contain a universal vertex. Discrete Math. 312 1652–1657.CrossRefGoogle Scholar
[9]Bonato, A. and Nowakowski, R. (2011) The Game of Cops and Robbers on Graphs, American Mathematical Society.Google Scholar
[10]Bonato, A., Prałat, P. and Wang, C. (2007) Pursuit-evasion in models of complex networks. Internet Mathematics 4 419–436.Google Scholar
[11]Cooper, C. and Frieze, A. (2011) The cover time of random geometric graphs. Random Struct. Alg. 38 324–349.Google Scholar
[12]Frankl, P. (1987) Cops and robbers in graphs with large girth and Cayley graphs. Discrete Appl. Math. 17 301–305.CrossRefGoogle Scholar
[13]Frankl, P. (1987) On a pursuit game on Cayley graphs. Combinatorica 7 67–70.Google Scholar
[14]Frieze, A., Krivelevich, M. and Lo, P.-S. (2012) Variations on cops and robbers. J. Graph Theory 69 383–402.Google Scholar
[15]Guibas, L. J., Latombe, J.-C., Lavalle, S. M., Lin, D. and Motwani, R. (1996) A visibility-based pursuit-evasion problem. Internat. J. Comput. Geometry Appl. 9 471–494.Google Scholar
[16]Gupta, P. and Kumar, P. R. (1999) Critical power for asymptotic connectivity in wireless networks. In Stochastic Analysis, Control, Optimization and Applications (McEneaney, W. M., Yin, G. G. and Zhang, Q., eds), Birkhäuser, pp. 547–566.CrossRefGoogle Scholar
[17]Hahn, G. (2007) Cops, robbers and graphs. Tatra Mountain Math. Publ. 36 163–176.Google Scholar
[18]Isler, V., Kannan, S. and Khanna, S. (2005) Randomized pursuit-evasion in a polygonal environment. IEEE Trans. Robotics 5 864–875.Google Scholar
[19]Kingman, J. (1993) Poisson Processes, Oxford University Press.Google Scholar
[20]Kopparty, S. and Ravishankar, C. V. (2005) A framework for pursuit evasion games in ℝn. Inf. Process. Lett. 96 114–122.Google Scholar
[21]Lavalle, S. M., Lin, D., Guibas, L. J., Latombe, J.-C. and Motwani, R. (1997) Finding an unpredictable target in a workspace with obstacles. In Proc. 1997 IEEE International Conference on Robotics and Automation, pp. 737–742.Google Scholar
[22]Lu, L. and Peng, X. (2011) On Meyniel's conjecture of the cop number. J. Graph Theory, doi: 10.1002/jgt.20642.Google Scholar
[23]Łuczak, T. and Prałat, P. (2010) Chasing robbers on random graphs: Zigzag theorem. Random Struct. Alg. 37 516–524.Google Scholar
[24]Mehrabian, A. (2011) The capture time of grids. Discrete Math. 311 102–105.Google Scholar
[25]Neufeld, S. and Nowakowski, R. (1998) A game of cops and robbers played on products of graphs. Discrete Math. 186 253–268.Google Scholar
[26]Nowakowski, R. and Winkler, P. (1983) Vertex-to-vertex pursuit in a graph. Discrete Math. 43 235–239.Google Scholar
[27]Penrose, M. D. (1997) The longest edge of the random minimal spanning tree. Ann. Appl. Probab. 7 340–361.Google Scholar
[28]Penrose, M. D. (2003) Random Geometric Graphs, Oxford University Press.CrossRefGoogle Scholar
[29]Prałat, P. (2010) When does a random graph have constant cop number? Australasian J. Combin. 46 285–296.Google Scholar
[30]Prałat, P. and Wormald, N. Meyniel's conjecture holds in random graphs. Submitted.Google Scholar
[31]Quilliot, A. (1978) Jeux et pointes fixes sur les graphes. PhD thesis, Université de Paris VI.Google Scholar
[32]Scott, A. and Sudakov, B. (2011) A bound for the cops and robbers problem. SIAM J. Discrete Math. 25 1438–1442.Google Scholar
[33]Sgall, J. (2001) A solution to David Gale's lion and man problem. Theoret. Comput. Sci. 259 663–670.Google Scholar
[34]Xue, F. and Kumar, P. R. (2006) Scaling Laws for Ad Hoc Wireless Networks: An Information Theoretic Approach, Vol. 1 of Foundations and Trends in Networking, Now Publishers Inc.Google Scholar