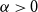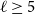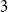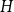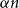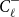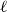The codegree Turán density of tight cycles minus one edge

Abstract

Given $\alpha \gt 0$ and an integer $\ell \geq 5$, we prove that every sufficiently large $3$-uniform hypergraph $H$ on $n$ vertices in which every two vertices are contained in at least $\alpha n$ edges contains a copy of $C_\ell ^{-}$, a tight cycle on $\ell$ vertices minus one edge. This improves a previous result by Balogh, Clemen, and Lidický.

1. Introduction

A $k$ -uniform hypergraph $H$ consists of a vertex set $V(H)$ together with a set of edges $E(H)\subseteq V(H)^{(k)}=\{S\subseteq V(H)\,:\,\vert S\vert =k\}$ . Throughout this note, if not stated otherwise, by hypergraph we always mean a $3$ -uniform hypergraph. Given a hypergraph $F$ , the extremal number of $F$ for $n$ vertices, $\textrm{ex}(n,F)$ , is the maximum number of edges an $n$ -vertex hypergraph can have without containing a copy of $F$ . Determining the value of $\textrm{ex}(n,F)$ , or the Turán density $\pi (F) = \lim _{n \to \infty } \frac{\textrm{ex}(n,F)}{\binom{n}{3}}$ , is one of the core problems in combinatorics. In particular, the problem of determining the Turán density of the complete $3$ -uniform hypergraph on four vertices, i.e., $\pi \left(K_4^{(3)}\right)$ , was asked by Turán in 1941 [13] and Erdős [4] offered 1000 $\$$ for its resolution. Despite receiving a lot of attention (see for instance the survey by Keevash [8]) this problem, and even the seemingly simpler problem of determining $\pi \left(K_4^{(3)-}\right)$ , where $K_4^{(3)-}$ is the $K_4^{(3)}$ minus one edge, remain open.

Several variations of this type of problem have been considered, see for instance [1, 7, 12] and the references therein. The one that we are concerned with in this note asks how large the minimum codegree of an $F$ -free hypergraph can be. Given a hypergraph $H$ and $S\subseteq V$ , we define the degree $d(S)$ of $S$ (in $H$ ) as the number of edges containing $S$ , i.e., $d(S)=\vert \{e\in E(H)\,:\,S\subseteq e\}\vert$ . If $S=\{v\}$ or $S=\{u,v\}$ (and $H$ is $3$ -uniform), we omit the parentheses and speak of $d(v)$ or $d(uv)$ as the degree of $v$ or codegree of $u$ and $v$ , respectively. We further write $\delta (H)=\delta _1(H)=\min _{v\in V(H)} d(v)$ and $\delta _2(H)=\min _{uv\in V(H)^{(2)}}d(uv)$ for the minimum degree and the minimum codegree of $H$ , respectively.

Given a hypergraph $F$ and $n\in \mathbb{N}$ , Mubayi and Zhao [11] introduced the codegree Turán number $\textrm{ex}_2(n,F)$ of $n$ and $F$ as the maximum $d$ such that there is an $F$ -free hypergraph $H$ on $n$ vertices with $\delta _2(H)\geq d$ . Moreover, they defined the codegree Turán density of $F$ as

\begin{equation*}\gamma (F) \,:\!=\, \lim _{n\to \infty } \frac {ex_2(n,F)}{n}\,\end{equation*}

and proved that this limit always exists. It is not hard to see that

\begin{equation*}\gamma (F) \leq \pi (F)\,.\end{equation*}

The codegree Turán density is known only for a few (non-trivial) hypergraphs (and blow-ups of these), see the table in [1]. The first result that determined $\gamma (F)$ exactly is due to Mubayi [9] who showed that $\gamma (\mathbb F) = 1/2$ , where $\mathbb F$ denotes the ‘Fano plane’. Later, using a computer assisted proof, Falgas–Ravry, Pikhurko, Vaughan, and Volec [6] proved that $\gamma \left(K_4^{(3)-}\right)=1/4$ . As far as we know, the only other hypergraph for which the codegree Turán density is known is $F_{3,2}$ , a hypergraph with vertex set [5] and edges $123$ , $124$ , $125$ , and $345$ [5]. The problem of determining the codegree Turán density of $K_4^{(3)}$ remains open, and Czygrinow and Nagle [2] conjectured that $\gamma \left(K_4^{(3)}\right)=1/2$ . For more results concerning $\pi (F)$ , $\gamma (F)$ , and other variations of the Turán density see [1].

Given an integer $\ell \geq 3$ , a tight cycle $C_\ell$ is a hypergraph with vertex set $\{v_1, \dots, v_\ell \}$ and edge set $\{v_iv_{i+1}v_{i+2}\,:\,i\in \mathbb{Z}/\ell \mathbb{Z}\}$ . Moreover, we define $C_\ell ^{-}$ as $C_\ell ^{}$ minus one edge. In this note, we prove that the Turán codegree density of $C_\ell ^{-}$ is zero for every $\ell \geq 5$ .

Theorem 1.1. Let $\ell \geq 5$ be an integer. Then $\gamma \left(C_{\ell }^{-}\right)=0$ .

The previously known best upper bound was given by Balogh, Clemen, and Lidický [1] who used flag algebras to prove that $\gamma \left(C_{\ell }^-\right)\leq 0.136$ .

2. Proof of Theorem 1.1

For singletons, pairs, and triples, we may omit the set parentheses and commas. For a hypergraph $H=(V,E)$ and $v\in V$ , the link of $v$ (in $H$ ) is the graph $L_v=(V\setminus v,\{e\setminus v\,:\,v\in e\in E\})$ . For $x,y\in V$ , the neighbourhood of $x$ and $y$ (in $H$ ) is the set $N(xy)=\{z\in V\,:\,xyz\in E\}$ . For positive integers $\ell, k$ and a hypergraph $F$ on $k$ vertices, denote the $\ell$ -blow-up of $F$ by $F(\ell )$ . This is the $k$ -partite hypergraph $F(\ell )=(V, E)$ with $V = V_1 \dot \cup \dots \dot \cup V_k$ , $|V_i| = \ell$ for $1\leq i \leq k$ , and $E = \{v_{i_1}v_{i_2} v_{i_3}\,:\, v_{i_j} \in V_{i_j} \text{ and } i_1 i_2 i_3 \in E(F)\}$ .

In their seminal paper, Mubayi and Zhao [11] proved the following supersaturation result for the codegree Turán density.

Proposition 2.1 (Mubayi and Zhao [11]). For every hypergraph $F$ and $\varepsilon \gt 0$ , there are $n_0$ and $\delta \gt 0$ such that every hypergraph $H$ on $n\geq n_0$ vertices with $\delta _2(H)\geq (\gamma (F)+\varepsilon )n$ contains at least $\delta n^{v(F)}$ copies of $F$ . Consequently, for every positive integer $\ell$ , $\gamma (F) = \gamma (F(\ell ))$ .

Proof of Theorem 1.1. We begin by noting that it is enough to show that $\gamma \left(C_5^-\right) = 0$ . Indeed, we shall prove by induction that $\gamma \left(C_{\ell }^-\right)=0$ for every $\ell \geq 5$ . For $\ell =6$ , the result follows since $C_6^-$ is a subgraph of $C_3(2)$ . Hence, by Proposition 2.1, we have $\gamma \left(C_6^-\right)\leq \gamma (C_3(2))=\gamma (C_3)=0$ . For $\ell =7$ , note that $C_7^-$ is a subgraph of $C_5^-(2)$ . To see that, let $v_1,\dots,v_5$ be the vertices of a $C_5^-$ with edge set $\{v_iv_{i+1}v_{i+2}\,:\,i\neq 4\}$ , where the indices are taken modulo $5$ . Now add one copy $v^{\prime}_2$ of $v_2$ and one copy $v^{\prime}_3$ of $v_3$ . Then $v_1v_3v_2v_4v^{\prime}_3v_5v^{\prime}_2$ is the cyclic ordering of a $C_7^-$ with the missing edge being $v^{\prime}_3v_5v^{\prime}_2$ . Therefore, if $\gamma \left(C_5^-\right)=0$ , then, by Proposition 2.1, we have $\gamma \left(C_7^-\right)=0$ . Finally, for $\ell \geq 8$ , $\gamma \left(C_\ell ^-\right)=0$ follows by induction using the same argument and observing that $C_\ell ^-$ is a subgraph of $C_{\ell -3}^-(2)$ .

Given $\varepsilon \in (0,1)$ , consider a hypergraph $H=(V,E)$ on $n\geq \big (\frac{2}{\varepsilon }\big )^{5/\varepsilon ^2+2}$ vertices with $\delta _2(H)\geq \varepsilon n$ . We claim that $H$ contains a copy of a $C_5^-$ .

Given $v,b\in V$ , $S\subseteq V$ , and $P\subseteq (V\setminus S)^{2}$ , we say that $(v,S,b,P)$ is a nice picture if it satisfies the following (see Figure 1):

1. (i) $S\subseteq N_{L_v}(b)$ , where $N_{L_v}(b)$ is the neighbourhood of $b$ in the link $L_v$ .

2. (ii) For every vertex $u\in S$ and ordered pair $(x,y)\in P$ , the sequence $ubxy$ is a path of length $3$ in $L_v$ .

Note that if $(v,S,b,P)$ is a nice picture and there exists $u\in S$ and $(x,y)\in P$ such that $uxy\in E$ , then $ubvxy$ is a copy of $C_5^-$ (with the missing edge being $yub$ )

Figure 1. A nice picture $(v,S,b,P)$ .

To find such a copy of $C_5^-$ in $H$ , we are going to construct a sequence of nested sets $S_t\subseteq S_{t-1}\subseteq \ldots \subseteq S_0$ , where $t=\lceil 5/\varepsilon ^2+1\rceil$ , such that for $1\leq i\leq t$ there are nice pictures $(v_i,S_i,b_i,P_i)$ satisfying $v_i\in S_{i-1}$ , $|S_i|\geq \big (\frac{\varepsilon }{2}\big )^{i+1}n\geq 1$ and $|P_i|\geq \varepsilon ^2 n^2/5$ . Suppose that such a sequence exists. Then by the pigeonhole principle, there exist two indices $i,j \in [t]$ such that $P_i\cap P_j\neq \emptyset$ and $i\lt j$ . Let $(x,y)$ be an element of $P_i\cap P_j$ . Hence, we obtain a nice picture $(v_i,S_i,b_i,P_i)$ , $v_j\in S_i$ and $(x,y)\in P_i$ such that $v_jxy \in E$ (since $xy$ is an edge in $L_{v_j}$ ). Consequently, $v_jb_iv_ixy$ is a copy of $C_5^-$ in $H$ .

It remains to prove that the sequence described above always exists. We construct it recursively. Let $S_0\subseteq V$ be an arbitrary subset of size $\varepsilon n/2$ . Suppose we already found the sets $S_i$ for $0\leq i\lt k\leq t$ , with the respective nice pictures $(v_i,S_i,b_i,P_i)$ for $1\leq i\lt k$ . Now we want to construct $(v_k,S_k,b_k,P_k)$ . Pick $v_k\in S_{k-1}$ arbitrarily. The minimum codegree of $H$ implies that $\delta (L_{v_k})\geq \varepsilon n$ and thus for every $u\in S_{k-1}$ , we have that $d_{L_{v_k}}(u)\geq \varepsilon n$ . Observe that

\begin{align*} \sum _{b \in V\setminus v_k} \vert N_{L_{v_k}}( b)\cap S_{k-1}\vert = \sum _{u \in S_{k-1}\setminus v_k} d_{L_{v_k}}(u) \geq \varepsilon n \big (\vert S_{k-1}\vert -1\big ) \geq \Big (\frac{\varepsilon }{2}\Big )^{k+1}n^2 \end{align*}

and therefore, by an averaging argument there is a vertex $b_k\in V\setminus v_k$ such that the subset $S_k\,:\!=\,N_{L_{v_k}}(b_k)\cap S_{k-1}\subseteq S_{k-1}$ is of size at least $|S_k|\geq \big (\frac{\varepsilon }{2}\big )^{k+1} n$ . Let $P_k$ be all the pairs $(x,y) \in (V\setminus S_k)^2$ such that for every vertex $v\in S_k$ , the sequence $v,b_k,x,y$ forms a path of length $3$ in $L_{v_k}$ . Since $|S_k|\leq \varepsilon n/2$ and $\delta (L_{v_k})\geq \varepsilon n$ , it is easy to see that $|P_k|\geq (\varepsilon n/2)(\varepsilon n/2-1) \geq \varepsilon ^2n^2/5$ . That is to say $(v_k, S_k, b_k, P_k)$ is a nice picture satisfying the desired conditions.

3. Concluding remarks

A famous result by Erdős [3] asserts that a hypergraph $F$ satisfies $\pi (F)=0$ if $F$ is tripartite (i.e., $V(F)=X_1\dot \cup X_2 \dot \cup X_3$ and for every $e\in E(F)$ we have $\vert e\cap X_i\vert = 1$ for every $i\in [3]$ ). Note that if $H$ is tripartite, then every subgraph of $H$ is tripartite as well and there are tripartite hypergraphs $H$ with $\vert E(H) \vert =\tfrac{2}{9} \binom{\vert V(H)\vert }{3}$ . Therefore, if $F$ is not tripartite, then $\pi (F)\geq 2/9$ . In other words, Erdős’ result implies that there are no Turán densities in the interval $(0,2/9)$ . It would be interesting to understand the behaviour of the codegree Turán density in the range close to zero.

Question 3.1. Is it true that for every $\xi \in (0,1]$ , there exists a hypergraph $F$ such that

\begin{equation*} 0\lt \gamma (F)\leq \xi \text { ?} \end{equation*}

Mubayi and Zhao [11] answered this question affirmatively if we consider the codegree Turán density of a family of hypergraphs instead of a single hypergraph.

Since $C_5^{-}$ is not tripartite, we have that $\pi (C_5^{-})\geq 2/9$ . The following construction attributed to Mubayi and Rödl (see e.g. [1]) provides a better lower bound. Let $H=(V,E)$ be a $C_5^{-}$ -free hypergraph on $n$ vertices. Define a hypergraph $\widetilde H$ on $3n$ vertices with $V(\widetilde H)= V_1\dot \cup V_2\dot \cup V_3$ such that $\widetilde H[V_i]=H$ for every $i\in [3]$ plus all edges of the form $e=\{v_1,v_2,v_3\}$ with $v_i\in V_i$ . Then, it is easy to check that $\widetilde H$ is also $C_5^{-}$ -free. We may recursively repeat this construction starting with $H$ being a single edge and obtain an arbitrarily large $C_5^{-}$ -free hypergraph with density $1/4-o(1)$ . In fact, those hypergraphs are $C_\ell ^-$ -free for every $\ell$ not divisible by three. The following is a generalisation of a conjecture in [10].

Conjecture 3.2. If $\ell \geq 5$ is not divisible by three, then $\pi \left(C_\ell ^{-}\right) = \frac{1}{4}\,$ .