Article contents
A central limit theorem for additive functionals of increasing trees
Published online by Cambridge University Press: 08 March 2019
Abstract
A tree functional is called additive if it satisfies a recursion of the form 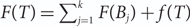 $F(T) = \sum_{j=1}^k F(B_j) + f(T)$, where B1, …, Bk are the branches of the tree T and f (T) is a toll function. We prove a general central limit theorem for additive functionals of d-ary increasing trees under suitable assumptions on the toll function. The same method also applies to generalized plane-oriented increasing trees (GPORTs). One of our main applications is a log-normal law that we prove for the size of the automorphism group of d-ary increasing trees, but other examples (old and new) are covered as well.
$F(T) = \sum_{j=1}^k F(B_j) + f(T)$, where B1, …, Bk are the branches of the tree T and f (T) is a toll function. We prove a general central limit theorem for additive functionals of d-ary increasing trees under suitable assumptions on the toll function. The same method also applies to generalized plane-oriented increasing trees (GPORTs). One of our main applications is a log-normal law that we prove for the size of the automorphism group of d-ary increasing trees, but other examples (old and new) are covered as well.
MSC classification
- Type
- Paper
- Information
- Combinatorics, Probability and Computing , Volume 28 , Special Issue 4: Analysis of Algorithms , July 2019 , pp. 618 - 637
- Copyright
- © Cambridge University Press 2019
Footnotes
An extended abstract of this paper was presented at the 27th International Conference on Probabilistic, Combinatorial and Asymptotic Methods for the Analysis of Algorithms, Kraków, 4–8 July 2016: see [15].
Supported by the Division for Research Development (DRD) of Stellenbosch University.
This material is based upon work supported by the National Research Foundation under grant number 96236.
References
- 6
- Cited by


