Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T16:09:59.627Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounded-Size Rules: The Barely Subcritical Regime

Published online by Cambridge University Press:  28 May 2014

SHANKAR BHAMIDI ,
AMARJIT BUDHIRAJA  and
XUAN WANG
SHANKAR BHAMIDI
Affiliation:
Department of Statistics and Operations Research, 304 Hanes Hall CB #3260, University of North Carolina, Chapel Hill, NC 27599, USA (e-mail: [email protected], [email protected], [email protected])
AMARJIT BUDHIRAJA
Affiliation:
Department of Statistics and Operations Research, 304 Hanes Hall CB #3260, University of North Carolina, Chapel Hill, NC 27599, USA (e-mail: [email protected], [email protected], [email protected])
XUAN WANG
Affiliation:
Department of Statistics and Operations Research, 304 Hanes Hall CB #3260, University of North Carolina, Chapel Hill, NC 27599, USA (e-mail: [email protected], [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Bounded-size rules (BSRs) are dynamic random graph processes which incorporate limited choice along with randomness in the evolution of the system. Typically one starts with the empty graph and at each stage two edges are chosen uniformly at random. One of the two edges is then placed into the system according to a decision rule based on the sizes of the components containing the four vertices. For bounded-size rules, all components of size greater than some fixed K ≥ 1 are accorded the same treatment. Writing BSR(t) for the state of the system with ⌊nt/2⌋ edges, Spencer and Wormald [26] proved that for such rules, there exists a (rule-dependent) critical time tc such that when t < tc the size of the largest component is of order log n, while for t > tc, the size of the largest component is of order n. In this work we obtain upper bounds (that hold with high probability) of order n2γ log4n, on the size of the largest component, at time instants tn = tc−n−γ, where γ ∈ (0,1/4). This result for the barely subcritical regime forms a key ingredient in the study undertaken in [4], of the asymptotic dynamic behaviour of the process describing the vector of component sizes and associated complexity of the components for such random graph models in the critical scaling window. The proof uses a coupling of BSR processes with a certain family of inhomogeneous random graphs with vertices in the type space 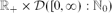$\mathbb{R}_+\times \mathcal{D}([0,\infty):\mathbb{N}_0)$, where 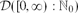$\mathcal{D}([0,\infty):\mathbb{N}_0)$ is the Skorokhod D-space of functions that are right continuous and have left limits, with values in the space of non-negative integers 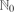$\mathbb{N}_0$, equipped with the usual Skorokhod topology. The coupling construction also gives an alternative characterization (from the usual explosion time of the susceptibility function) of the critical time tc for the emergence of the giant component in terms of the operator norm of integral operators on certain L2 spaces.

Keywords

Primary 60C05Secondary 05C8090B15
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 4 , July 2014 , pp. 505 - 538
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Achlioptas, D., D'Souza, R. M. and Spencer, J. (2009) Explosive percolation in random networks. Science 323 1453.CrossRefGoogle ScholarPubMed
[2]Aldous, D. (1997) Brownian excursions, critical random graphs and the multiplicative coalescent. Ann. Probab. 25 812–854.CrossRefGoogle Scholar
[3]Bhamidi, S., Budhiraja, A. and Wang, X. (2013) Aggregation models with limited choice and the multiplicative coalescent. Random Struct. Alg. http://dx.doi.org/10.1002/rsa.20493CrossRefGoogle Scholar
[4]Bhamidi, S., Budhiraja, A. and Wang, X. (2013) The augmented multiplicative coalescent, bounded size rules and critical dynamics of random graphs. Probab Theory Rel. Fields, 1–64. http://dx.doi.org/10.1007/s00440-013-0540-xGoogle Scholar
[5]Bohman, T. and Frieze, A. (2001) Avoiding a giant component. Random Struct. Alg. 19 75–85.CrossRefGoogle Scholar
[6]Bohman, T., Frieze, A. and Wormald, N.C. (2004) Avoidance of a giant component in half the edge set of a random graph. Random Struct. Alg. 25 432–449.CrossRefGoogle Scholar
[7]Bollobás, B. (2001) Random Graphs, second edition, Vol. 73 of Cambridge Studies in Advanced Mathematics, Cambridge University Press.CrossRefGoogle Scholar
[8]Bollobás, B., Janson, S. and Riordan, O. (2007) The phase transition in inhomogeneous random graphs. Random Struct. Alg. 31 3–122.CrossRefGoogle Scholar
[9]Brémaud, P. (1981) Point Processes and Queues, Springer.CrossRefGoogle Scholar
[10]Ding, J., Lubetzky, E. and Peres, Y. (2012) Mixing time of near-critical random graphs. Ann. Probab. 40 979–1008.CrossRefGoogle Scholar
[11]Erdős, P. and Rényi, A. (1960) On the evolution of random graphs. Magyar Tud. Akad. Mat. Kutató Int. Közl. 5 17–61.Google Scholar
[12]Erdős, P. and Rényi, A. (1961) On the evolution of random graphs. Bull. Inst. Internat. Statist. 38 343–347.Google Scholar
[13]van der Hofstad, R. and Nachmias, A. (2012) Hypercube percolation. arXiv:1201.3953. To appear in Metrika.Google Scholar
[14]Janson, S. (2008) The largest component in a subcritical random graph with a power law degree distribution. Ann. Appl. Probab. 18 1651–1668.CrossRefGoogle Scholar
[15]Janson, S. and Luczak, M. J. (2008) Susceptibility in subcritical random graphs. J. Math. Phys. 49 125207.CrossRefGoogle Scholar
[16]Janson, S. and Spencer, J. (2012) Phase transitions for modified Erdős–Rényi processes. Arkiv för Matematik 50 305–329.CrossRefGoogle Scholar
[17]Janson, S., Knuth, D., Luczak, T. and Pittel, B. (1994) The birth of the giant component (with an introduction by the editors). Random Struct. Alg. 4 231–358.Google Scholar
[18]Kang, M., Perkins, W. and Spencer, J. (2013) The Bohman–Frieze process near criticality. Random Struct. Alg. 43 221–250.CrossRefGoogle Scholar
[19]Kim, J. H. (2006) Poisson cloning model for random graphs. In Proc. International Congress of Mathematicians, Vol. III, European Mathematical Society, pp. 873–897.Google Scholar
[20]Liptser, R. S. and Shiryayev, A. N. (1989) Theory of Martingales, Vol. 49 of Mathematics and its Applications (Soviet Series), Kluwer Academic. Translated from the Russian by K. Dzjaparidze (Kacha Dzhaparidze).CrossRefGoogle Scholar
[21]Norris, J. R. (1998) Markov Chains, Vol. 2 of Cambridge Series in Statistical and Probabilistic Mathematics, Cambridge University Press.Google Scholar
[22]Pittel, B. G. (2008) On the largest component of a random graph with a subpower-law degree sequence in a subcritical phase. Ann. Appl. Probab. 18 1636–1650.CrossRefGoogle Scholar
[23]Riordan, O. and Warnke, L. (2012) Achlioptas process phase transitions are continuous. Ann. Appl. Probab. 22 1450–1464.CrossRefGoogle Scholar
[24]Riordan, O. and Warnke, L. (2014) The evolution of subcritical Achlioptas processes. Random Struct. Alg. http://dx.doi.org/10.1002/rsa.20530Google Scholar
[25]Sen, S. (2013) On the largest component in the subcritical regime of the Bohman–Frieze process. arXiv:1307.2041Google Scholar
[26]Spencer, J. and Wormald, N.. (2007) Birth control for giants. Combinatorica 27 587–628.CrossRefGoogle Scholar