Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Martin, Greg
and
O’Bryant, Kevin
2009.
The supremum of autoconvolutions, with applications to additive number theory.
Illinois Journal of Mathematics,
Vol. 53,
Issue. 1,
Cilleruelo, Javier
Ruzsa, Imre
and
Vinuesa, Carlos
2010.
Generalized Sidon sets.
Advances in Mathematics,
Vol. 225,
Issue. 5,
p.
2786.
Matolcsi, Máté
and
Vinuesa, Carlos
2010.
Improved bounds on the supremum of autoconvolutions.
Journal of Mathematical Analysis and Applications,
Vol. 372,
Issue. 2,
p.
439.
Cilleruelo, Javier
2010.
Sidon sets in Nd.
Journal of Combinatorial Theory, Series A,
Vol. 117,
Issue. 7,
p.
857.
Cloninger, Alexander
and
Steinerberger, Stefan
2017.
On suprema of autoconvolutions with an application to Sidon sets.
Proceedings of the American Mathematical Society,
Vol. 145,
Issue. 8,
p.
3191.


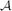 is called a
is called a 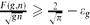 where ϵ
where ϵ