Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-18T19:57:02.005Z Has data issue: false hasContentIssue false
  • English
  • Français

Average-case complexity of the Euclidean algorithm with a fixed polynomial over a finite field

Part of: Algorithms - Computer Science General field theory Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  06 July 2021

Nardo Giménez ,
Guillermo Matera ,
Mariana Pérez  and
Melina Privitelli
Nardo Giménez
Affiliation:
Universidad Nacional de General Sarmiento, Instituto del Desarrollo Humano, J.M. Gutiérrez 1150 (B1613GSX) Los Polvorines, Buenos Aires, Argentina
Guillermo Matera*
Affiliation:
Universidad Nacional de General Sarmiento, Instituto del Desarrollo Humano, J.M. Gutiérrez 1150 (B1613GSX) Los Polvorines, Buenos Aires, Argentina Universidad de Buenos Aires, Facultad de Ciencias Exactas y Naturales, Departamento de Matemática, Ciudad Universitaria, Pabellón I (1428) Buenos Aires, Argentina Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina
Mariana Pérez
Affiliation:
Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina Universidad Nacional de Hurlingham, Instituto de Tecnología e Ingeniería, Av. Gdor. Vergara 2222 (B1688GEZ), Villa Tesei, Buenos Aires, Argentina
Melina Privitelli
Affiliation:
Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina Universidad Nacional de General Sarmiento, Instituto de Ciencias, J.M. Gutiérrez 1150 (B1613GSX) Los Polvorines, Buenos Aires, Argentina
*
*Corresponding author. Emails:[email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse the behaviour of the Euclidean algorithm applied to pairs (g,f) of univariate nonconstant polynomials over a finite field 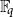$\mathbb{F}_{q}$ of q elements when the highest degree polynomial g is fixed. Considering all the elements f of fixed degree, we establish asymptotically optimal bounds in terms of q for the number of elements f that are relatively prime with g and for the average degree of 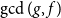$\gcd(g,f)$ . We also exhibit asymptotically optimal bounds for the average-case complexity of the Euclidean algorithm applied to pairs (g,f) as above.

Keywords

Finite fieldsrational pointsEuclidean algorithmsymmetric functionsresultantaverage-case complexity

MSC classification

Primary: 12E20: Finite fields (field-theoretic aspects)
Secondary: 14G05: Rational points 14G15: Finite ground fields 68W40: Analysis of algorithms
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 1 , January 2022 , pp. 166 - 183
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

The authors were partially supported by the grants PIP CONICET 11220130100598 and PIO CONICET-UNGS 14420140100027

References

Basu, S., Pollack, R. and Roy, M.-F. (2006) Algorithms in Real Algebraic Geometry, 2nd ed. Algorithms Comput. Math., Vol. 10, Springer.CrossRefGoogle Scholar
Berthé, V., Nakada, H., Natsui, R. and Vallée, B. (2014) Fine costs for Euclid’s algorithm on polynomials and Farey maps. Adv. Appl. Math. 54 27–65.CrossRefGoogle Scholar
Cafure, A. and Matera, G. (2006) Improved explicit estimates on the number of solutions of equations over a finite field. Finite Fields Appl. 12 155–185.CrossRefGoogle Scholar
Flajolet, P. and Sedgewick, R. (2009) Analytic Combinatorics. Cambridge University Press.CrossRefGoogle Scholar
Fulton, W. (1984) Intersection Theory. Springer.CrossRefGoogle Scholar
von zur Gathen, J. and Gerhard, J. (1999) Modern Computer Algebra. Cambridge University Press.Google Scholar
Graham, R., Knuth, D. and Patashnik, O.(1994) Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Addison–Wesley.Google Scholar
Heintz, J. (1983) Definability and fast quantifier elimination in algebraically closed fields. Theoret. Comput. Sci. 24 239–277.CrossRefGoogle Scholar
Heydtmann, A. and Jensen, J. (2000) On the equivalence of the Berlekamp–Massey and the Euclidean algorithms for decoding. IEEE Trans. Inform. Theory 46 2614–2624.Google Scholar
Knuth, D. E. (1981) The Art of Computer Programming II: Semi–Numerical Algorithms, Vol. 2. Addison-Wesley.Google Scholar
Lascoux, A. (2003) Symmetric Functions and Combinatorial Operators on Polynomials. CBMS Reg. Conf. Ser. Math., Vol. 99, American Mathematical Society.Google Scholar
Lhote, L. and Vallée, B. (2008) Gaussian laws for the main parameters of the Euclid algorithms. Algorithmica 50 497–554.CrossRefGoogle Scholar
Ma, K. and von zur Gathen, J. (1990) Analysis of Euclidean algorithms for polynomials over finite fields. J. Symb. Comput. 9 429–455.CrossRefGoogle Scholar
Norton, G. (1989) Precise analyses of the right- and left-shift greatest common divisor algorithms for GF(q)[x]. SIAM J. Comput. 18 608–624.CrossRefGoogle Scholar