Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T15:27:39.055Z Has data issue: false hasContentIssue false
  • English
  • Français

An Improved Upper Bound for Bootstrap Percolation in All Dimensions

Part of: Combinatorial probability Special processes

Published online by Cambridge University Press:  17 June 2019

Andrew J. Uzzell
Andrew J. Uzzell*
Affiliation:
Department of Mathematics and Statistics, Grinnell College, Grinnell, IA 50112, USA
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In r-neighbour bootstrap percolation on the vertex set of a graph G, a set A of initially infected vertices spreads by infecting, at each time step, all uninfected vertices with at least r previously infected neighbours. When the elements of A are chosen independently with some probability p, it is natural to study the critical probability pc(G, r) at which it becomes likely that all of V(G) will eventually become infected. Improving a result of Balogh, Bollobás and Morris, we give a bound on the second term in the expansion of the critical probability when G = [n]d and d ⩾ r ⩾ 2. We show that for all d ⩾ r ⩾ 2 there exists a constant cd,r > 0 such that if n is sufficiently large, then

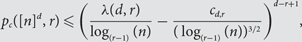$$p_c (\left[ n \right]^d ,{\rm{ }}r){\rm{\le }}\left( {\frac{{\lambda (d,r)}}{{\log _{(r - 1)} (n)}} - \frac{{c_{d,r} }}{{(\log _{(r - 1)} (n))^{3/2} }}} \right)^{d - r + 1} ,$$

where λ(d, r) is an exact constant and log(k) (n) denotes the k-times iterated natural logarithm of n.

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 60C05: Combinatorial probability
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 28 , Issue 6 , November 2019 , pp. 936 - 960
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

This work was done while the author was at the University of Memphis.

References

Adler, J. and Lev, U. (2003) Bootstrap percolation: Visualizations and applications. Braz. J. Phys. 33 641–644.CrossRefGoogle Scholar
Aizenman, M. and Lebowitz, J. L. (1988) Metastability effects in bootstrap percolation. J. Phys. A 21 3801–3813.CrossRefGoogle Scholar
Balister, P., Bollobás, B., Przykucki, M. and Smith, P. (2016) Subcritical U-bootstrap percolation models have non-trivial phase transitions. Trans. Amer. Math. Soc. 368 7385–7411.CrossRefGoogle Scholar
Balogh, J., Bollobás, B., Duminil-Copin, H. and Morris, R. (2012) The sharp threshold for bootstrap percolation in all dimensions. Trans. Amer. Math. Soc. 364 2667–2701.CrossRefGoogle Scholar
Balogh, J., Bollobás, B. and Morris, R. (2009) Bootstrap percolation in three dimensions. Ann. Probab. 37 1329–1380.CrossRefGoogle Scholar
Balogh, J. and Pete, G. (1998) Random disease on the square grid. Random Struct. Alg. 134 409–422.3.0.CO;2-U>CrossRefGoogle Scholar
Bollobás, B., Duminil-Copin, H., Morris, R. and Smith, P. (2019) Universality of two-dimensional critical cellular automata. Proc. London Math. Soc., to appear.Google Scholar
Bollobás, B., Duminil-Copin, H., Morris, R. and Smith, P. (2017) The sharp threshold for the Duarte model. Ann. Probab. 45 4222–4272.CrossRefGoogle Scholar
Bollobás, B., Smith, P. J. and Uzzell, A. J. (2015) Monotone cellular automata in a random environment. Combin. Probab. Comput. 24 687–722.CrossRefGoogle Scholar
Cerf, R. and Cirillo, E. N. M. (1999) Finite size scaling in three-dimensional bootstrap percolation. Ann. Probab. 27 1837–1850.CrossRefGoogle Scholar
Cerf, R. and Manzo, F. (2002) The threshold regime of finite volume bootstrap percolation. Stoch. Process. Appl. 101 69–82.CrossRefGoogle Scholar
Chalupa, J., Leath, P. L. and Reich, G. R. (1979) Bootstrap percolation on a Bethe lattice. J. Phys. C 12 L31–L35.CrossRefGoogle Scholar
Duminil-Copin, H. and Holroyd, A. E. (2012) Finite volume Bootstrap Percolation with balanced threshold rules on Z2 http://www.ihes.fr/~duminil/Google Scholar
Duminil-Copin, H. and van Enter, A. C. D. (2013) Sharp metastability threshold for an anisotropic bootstrap percolation model. Ann. Probab. 41 1218–1242.CrossRefGoogle Scholar
Duminil-Copin, H., van Enter, A. C. D. and Hulshof, T. (2018) Higher order corrections for anisotropic bootstrap percolation. Probab. Theory Related Fields 172 191–243.CrossRefGoogle Scholar
Fontes, L. R., Schonmann, R. H. and Sidoravicius, V. (2002) Stretched exponential fixation in stochastic Ising models at zero temperature. Comm. Math. Phys. 228 495–518.CrossRefGoogle Scholar
Gravner, J. and Holroyd, A. E. (2008) Slow convergence in bootstrap percolation. Ann. Appl. Probab. 18 909–928.CrossRefGoogle Scholar
Gravner, J., Holroyd, A. E. and Morris, R. (2012) A sharper threshold for bootstrap percolation in two dimensions. Probab. Theory Related Fields 153 1–23.CrossRefGoogle Scholar
Harris, T. E. (1960) A lower bound for the critical probability in a certain percolation process. Math. Proc. Cambridge Philos. Soc. 26 13–20.CrossRefGoogle Scholar
Hartarsky, I. and Morris R. (2018) The second term for two-neighbour bootstrap percolation in two dimensions. Trans. Amer. Math. Soc.CrossRefGoogle Scholar
Holroyd, A. E. (2003) Sharp metastability threshold for two-dimensional bootstrap percolation. Probab. Theory Related Fields 125 195–224.CrossRefGoogle Scholar
Holroyd, A. E. (2006) The metastability threshold for modified bootstrap percolation in d dimensions. Electron. J. Probab. 11 418–433.CrossRefGoogle Scholar
Morris, R. (2011) Zero-temperature Glauber dynamics on Zd. Probab. Theory Related Fields 149 417–434.CrossRefGoogle Scholar
Schonmann, R. H. (1992) On the behavior of some cellular automata related to bootstrap percolation. Ann. Probab. 20 174–193.CrossRefGoogle Scholar
van Enter, A. C. D. (1987) Proof of Straley’s argument for bootstrap percolation. J. Statist. Phys. 48 943–945.CrossRefGoogle Scholar
van Enter, A. C. D. and Fey, A. (2012) Metastability threshold for anisotropic bootstrap percolation in three dimensions. J. Statist. Phys. 147 97–112.CrossRefGoogle Scholar