Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T11:37:42.436Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost Spanning Subgraphs of Random Graphs After Adversarial Edge Removal

Published online by Cambridge University Press:  08 August 2013

JULIA BÖTTCHER ,
YOSHIHARU KOHAYAKAWA  and
ANUSCH TARAZ
JULIA BÖTTCHER
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, Rua do Matão 1010, 05508–090 São Paulo, Brazil (e-mail: [email protected])
YOSHIHARU KOHAYAKAWA
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, Rua do Matão 1010, 05508–090 São Paulo, Brazil (e-mail: [email protected])
ANUSCH TARAZ
Affiliation:
Zentrum Mathematik, Technische Universität München, Boltzmannstraße 3, D–85747 Garching bei München, Germany (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

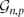Let Δ ≥ 2 be a fixed integer. We show that the random graph ${\mathcal{G}_{n,p}}$ with 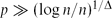$p\gg (\log n/n)^{1/\Delta}$ is robust with respect to the containment of almost spanning bipartite graphs H with maximum degree Δ and sublinear bandwidth in the following sense: asymptotically almost surely, if an adversary deletes arbitrary edges from 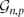${\mathcal{G}_{n,p}}$ in such a way that each vertex loses less than half of its neighbours, then the resulting graph still contains a copy of all such H.

Keywords

Primary 05C35Secondary 05C8005C60
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 5 , September 2013 , pp. 639 - 683
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Albert, M., Frieze, A. and Reed, B. (1995) Multicoloured Hamilton cycles. Electron. J. Combin. 2 13 pp.CrossRefGoogle Scholar
[2]Alon, N. and Capalbo, M. (2007) Sparse universal graphs for bounded-degree graphs. Random Struct. Alg. 31 123–133.CrossRefGoogle Scholar
[3]Alon, N. and Capalbo, M. (2008) Optimal universal graphs with deterministic embedding. In Proc. 19th Annual ACM–SIAM Symposium on Discrete Algorithms: SODA, pp. 373–378.Google Scholar
[4]Alon, N., Capalbo, M., Kohayakawa, Y., Rödl, V., Ruciński, A. and Szemerédi, E. (2000) Universality and tolerance. In Proc. 41st Annual Symposium on Foundations of Computer Science: FOCS, pp. 14–21.CrossRefGoogle Scholar
[5]Alon, N., Krivelevich, M. and Sudakov, B. (2007) Embedding nearly-spanning bounded degree trees. Combinatorica 27 629–644.Google Scholar
[6]Balogh, J., Csaba, B. and Samotij, W. (2011) Local resilience of almost spanning trees in random graphs. Random Struct. Alg. 38 121–139.Google Scholar
[7]Balogh, J., Lee, C. and Samotij, W. (2012) Corrádi and Hajnal's theorem for sparse random graphs. Combin. Probab. Comput. 21 23–55.Google Scholar
[8]Böttcher, J., Kohayakawa, Y. and Taraz, A. Almost spanning subgraphs of random graphs after adversarial edge removal. arXiv:1003.0890Google Scholar
[9]Böttcher, J., Kohayakawa, Y. and Procacci, A. (2012) Properly coloured copies and rainbow copies of large graphs with small maximum degree. Random Struct. Alg. 40 425–436.CrossRefGoogle Scholar
[10]Böttcher, J., Pruessmann, K. P., Taraz, A. and Würfl, A. (2010) Bandwidth, expansion, treewidth, separators and universality for bounded-degree graphs. Europ. J. Combin. 31 1217–1227.CrossRefGoogle Scholar
[11]Böttcher, J., Schacht, M. and Taraz, A. (2009) Proof of the bandwidth conjecture of Bollobás and Komlós. Math. Ann. 343 175–205.CrossRefGoogle Scholar
[12]Dellamonica, D., Kohayakawa, Y., Marciniszyn, M. and Steger, A. (2008) On the resilience of long cycles in random graphs. Electron. J. Combin. 15 R32.Google Scholar
[13]Dellamonica, D., Kohayakawa, Y., Rödl, V. and Ruciński, A. (2008) Universality of random graphs. In Proc. 19th Annual ACM–SIAM Symposium on Discrete Algorithms: SODA, pp. 782–788.Google Scholar
[14]Dellamonica, D. Jr, Kohayakawa, Y., Rödl, V. and Ruciński, A. (2012) An improved upper bound on the density of universal random graphs. In LATIN 2012, Vol. 7256 of Lecture Notes in Computer Science, Springer, pp. 231–242.Google Scholar
[15]Dirac, G. A. (1952) Some theorems on abstract graphs. Proc. London Math. Soc. (3) 2 69–81.CrossRefGoogle Scholar
[16]Erdős, P., Nešetřil, J. and Rödl, V. (1983) On some problems related to partitions of edges of a graph. In Graphs and Other Combinatorial Topics: Prague 1982, Teubner, pp. 54–63.Google Scholar
[17]Frieze, A. and Reed, B. (1993) Polychromatic Hamilton cycles. Discrete Math. 118 69–74.Google Scholar
[18]Gerke, S., Kohayakawa, Y., Rödl, V. and Steger, A. (2007) Small subsets inherit sparse ε-regularity. J. Combin. Theory Ser. B 97 34–56.Google Scholar
[19]Hahn, G. and Thomassen, C. (1986) Path and cycle sub-Ramsey numbers and an edge-colouring conjecture. Discrete Math. 62 29–33.Google Scholar
[20]Hajnal, A. and Szemerédi, E. (1970) Proof of a conjecture of P. Erdős. In Combinatorial Theory and its Applications II: Balatonfüred 1969, North-Holland, pp. 601–623.Google Scholar
[21]Huang, H., Lee, C. and Sudakov, B. (2012) Bandwidth theorem for random graphs. J. Combin. Theory Ser. B 102 14–37.Google Scholar
[22]Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley-Interscience.Google Scholar
[23]Kohayakawa, Y. (1997) Szemerédi's regularity lemma for sparse graphs. In Foundations of Computational Mathematics: Rio de Janeiro 1997, Springer, pp. 216–230.Google Scholar
[24]Kohayakawa, Y. and Rödl, V. (2003) Regular pairs in sparse random graphs I. Random Struct. Alg. 22 359–434.CrossRefGoogle Scholar
[25]Kohayakawa, Y. and Rödl, V. (2003) Szemerédi's regularity lemma and quasi-randomness. In Recent Advances in Algorithms and Combinatorics, Vol. 11 of CMS Books Math./Ouvrages Math. SMC., Springer, pp. 289–35.Google Scholar
[26]Kohayakawa, Y., Rödl, V., Schacht, M. and Szemerédi, E. (2011) Sparse partition universal graphs for graphs of bounded degree. Adv. Math. 226 5041–5065.CrossRefGoogle Scholar
[27]Rödl, V., Ruciński, A. and Taraz, A. (1999) Hypergraph packing and graph embedding. Combin. Probab. Comput. 8 363–376.CrossRefGoogle Scholar
[28]Sudakov, B. and Vu, V. (2008) Local resilience of graphs. Random Struct. Alg. 33 409–433.CrossRefGoogle Scholar
[29]Turán, P. (1941) Eine Extremalaufgabe aus der Graphentheorie. Mat. Fiz. Lapok 48 436–452.Google Scholar