Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T19:12:12.119Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost Isoperimetric Subsets of the Discrete Cube

Published online by Cambridge University Press:  17 February 2011

DAVID ELLIS
DAVID ELLIS*
Affiliation:
St John's College, Cambridge, UK (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

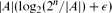We show that a set A ⊂ {0, 1}n with edge-boundary of size at most can be made into a subcube by at most (2ε/log2(1/ε))|A| additions and deletions, provided ε is less than an absolute constant.

We deduce that if A ⊂ {0, 1}n has size 2t for some t ∈ ℕ, and cannot be made into a subcube by fewer than δ|A| additions and deletions, then its edge-boundary has size at least provided δ is less than an absolute constant. This is sharp whenever δ = 1/2j for some j ∈ {1, 2, . . ., t}.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 20 , Issue 3 , May 2011 , pp. 363 - 380
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ben-Or, M. and Linial, N. (1985) Collective coin flipping, robust voting games, and minima of Banzhaf value. In Proc. 26th IEEE Symposium on the Foundations of Computer Science, pp. 408–416.Google Scholar
[2]Bernstein, A. J. (1967) Maximally connected arrays on the n-cube. SIAM J. Appl. Math. 15 1485–1489.CrossRefGoogle Scholar
[3]Falik, D. and Samorodnitsky, A. (2007) Edge-isoperimetric inequalities and influences. Combin. Probab. Comput. 16 693–712.CrossRefGoogle Scholar
[4]Friedgut, E. (1998) Boolean functions with low average sensitivity depend on few coordinates. Combinatorica 18 27–36.CrossRefGoogle Scholar
[5]Friedgut, E., Kalai, G. and Naor, A. (2002) Boolean functions whose Fourier transform is concentrated on the first two levels. Adv. Appl. Math. 29 427–437.CrossRefGoogle Scholar
[6]Harper, L. H. (1964) Optimal assignments of numbers to vertices. SIAM J. Appl. Math. 12 131–135.CrossRefGoogle Scholar
[7]Hart, S. (1976) A note on the edges of the n-cube. Discrete Math. 14 157–163.CrossRefGoogle Scholar
[8]Kahn, J. and Kalai, G. (2007) Thresholds and expectation thresholds. Combin. Probab. Comput. 16 495–502.CrossRefGoogle Scholar
[9]Kahn, J., Kalai, G. and Linial, N. (1988) The influence of variables on boolean functions. In FOCS 1988, pp. 68–80.CrossRefGoogle Scholar
[10]Keevash, P. (2008) Shadows and intersections: Stability and new proofs. Adv. Math. 218 1685–1703.CrossRefGoogle Scholar
[11]Leader, I. Personal communication.Google Scholar
[12]Lindsey, J. H. II (1964) Assignment of numbers to vertices. Amer. Math. Monthly 71 508–516.CrossRefGoogle Scholar
[13]Rossignol, R. (2005) Threshold for monotone symmetric properties through a logarithmic Sobolev inequality. Ann. Probab. 34 1707–1725.Google Scholar
[14]Samorodnitsky, A. (2009) Edge isoperimetric inequalities in the Hamming cube. Talk given at the IPAM Long Program in Combinatorics, Workshop IV: Analytical Methods in Combinatorics, Additive Number Theory and Computer Science, November 2009.Google Scholar
[15]Samorodnitsky, A. Personal communication.Google Scholar
[16]Talagrand, M. (1994) On Russo's approximate 0–1 law. Ann. Probab. 22 1576–1587.CrossRefGoogle Scholar