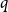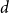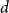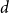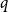1. Introduction
The
![]() $q$
-state Potts model on a graph
$q$
-state Potts model on a graph
![]() $G=(V,E)$
at inverse temperature
$G=(V,E)$
at inverse temperature
![]() $\beta$
is given by the partition function
$\beta$
is given by the partition function
where the sum is over all assignments of the spins
![]() $[q]=\{1,2,\dotsc,q\}$
to the vertices of
$[q]=\{1,2,\dotsc,q\}$
to the vertices of
![]() $G$
, and
$G$
, and
![]() $m(G,\sigma )$
is the number of edges such that both endpoints receive the same spin under
$m(G,\sigma )$
is the number of edges such that both endpoints receive the same spin under
![]() $\sigma$
. The Potts model has been of continued interest in combinatorics and computer science, most notably because of its direct relations to notions such as
$\sigma$
. The Potts model has been of continued interest in combinatorics and computer science, most notably because of its direct relations to notions such as
![]() $q$
-cuts and graph colourings. The Potts model also arises in physics and other areas as a generalisation of the Ising model. The main computational question associated to the Potts model is to approximate the partition function. The model is a canonical example of a Markov random field, and hence an excellent testbed for algorithmic techniques.
$q$
-cuts and graph colourings. The Potts model also arises in physics and other areas as a generalisation of the Ising model. The main computational question associated to the Potts model is to approximate the partition function. The model is a canonical example of a Markov random field, and hence an excellent testbed for algorithmic techniques.
The Potts model as above is ferromagnetic when
![]() $\beta \gt 0$
and antiferromagnetic when
$\beta \gt 0$
and antiferromagnetic when
![]() $\beta \lt 0$
. We are interested in the ferromagnetic model because for
$\beta \lt 0$
. We are interested in the ferromagnetic model because for
![]() $q\ge 3$
, at low temperatures approximating the partition function is #BIS-hard [Reference Goldberg and Jerrum16, Reference Galanis, Štefankovič, Vigoda and Yang19]. The complexity class known as #BIS consists of problems that are equivalent to counting the number of independent sets in bipartite graphs [Reference Dyer, Goldberg, Greenhill and Jerrum11], and understanding the complexity of approximating problems in #BIS is a longstanding problem. More precisely, approximating the partition function of the ferromagnetic Potts model for fixed
$q\ge 3$
, at low temperatures approximating the partition function is #BIS-hard [Reference Goldberg and Jerrum16, Reference Galanis, Štefankovič, Vigoda and Yang19]. The complexity class known as #BIS consists of problems that are equivalent to counting the number of independent sets in bipartite graphs [Reference Dyer, Goldberg, Greenhill and Jerrum11], and understanding the complexity of approximating problems in #BIS is a longstanding problem. More precisely, approximating the partition function of the ferromagnetic Potts model for fixed
![]() $\beta$
is #BIS-hard [Reference Goldberg and Jerrum16], and restricted to bounded-degree graphs it is #BIS-hard at low temperatures [Reference Galanis, Štefankovič, Vigoda and Yang19]. That is, for any
$\beta$
is #BIS-hard [Reference Goldberg and Jerrum16], and restricted to bounded-degree graphs it is #BIS-hard at low temperatures [Reference Galanis, Štefankovič, Vigoda and Yang19]. That is, for any
![]() $d\ge 3$
and
$d\ge 3$
and
![]() $q\ge 3$
, for any
$q\ge 3$
, for any
![]() $\beta \gt \beta _o(q,d)$
it is #BIS-hard to approximate
$\beta \gt \beta _o(q,d)$
it is #BIS-hard to approximate
![]() $Z_G(q,\beta )$
on graphs of maximum degree
$Z_G(q,\beta )$
on graphs of maximum degree
![]() $d$
, where
$d$
, where
![]() $\beta _o$
is given by
$\beta _o$
is given by
The parameter
![]() $\beta _o$
has a precise definition as the order-disorder threshold of the Potts model on the random
$\beta _o$
has a precise definition as the order-disorder threshold of the Potts model on the random
![]() $d$
-regular graph, and we note that it is not the same as the Gibbs uniqueness phase transition on the
$d$
-regular graph, and we note that it is not the same as the Gibbs uniqueness phase transition on the
![]() $d$
-regular tree. See e.g. [Reference Galanis, Štefankovič, Vigoda and Yang19, Reference Coja-Oghlan, Galanis, Goldberg, Ravelomanana, Stefankovic and Vigoda10] for a discussion of these thresholds. The Gibbs measure
$d$
-regular tree. See e.g. [Reference Galanis, Štefankovič, Vigoda and Yang19, Reference Coja-Oghlan, Galanis, Goldberg, Ravelomanana, Stefankovic and Vigoda10] for a discussion of these thresholds. The Gibbs measure
![]() $\mu _{G,q,\beta }$
for the Potts model on the spin assignments of
$\mu _{G,q,\beta }$
for the Potts model on the spin assignments of
![]() $G$
is given by
$G$
is given by
and, alongside approximating
![]() $Z$
, algorithms that approximately sample from
$Z$
, algorithms that approximately sample from
![]() $\mu _{G,q,\beta }$
are of interest in theoretical computer science. By self-reducibility, the standard problems of approximating the partition function and approximately sampling from the Gibbs measure are equivalent.
$\mu _{G,q,\beta }$
are of interest in theoretical computer science. By self-reducibility, the standard problems of approximating the partition function and approximately sampling from the Gibbs measure are equivalent.
Several recent works have given algorithms for #BIS-hard problems on random graphs or graphs with strong expansion [Reference Jenssen, Keevash and Perkins24, Reference Helmuth, Jenssen and Perkins21, Reference Galanis, Goldberg and Stewart14, Reference Chen, Galanis, Goldberg, Perkins, Stewart and Vigoda9]. One consequence of such research is a restriction on possible hard instances of #BIS, since under somewhat general conditions these works give efficient algorithms. In the absence of strong evidence that #BIS admits a general polynomial-time approximation algorithm, a weaker but intriguing prospect is that of a subexponential-time algorithm. The recent algorithm of Jenssen et al. [Reference Jenssen, Perkins and Potukuchi26] counts independent sets in
![]() $d$
-regular bipartite graphs in subexponential time when
$d$
-regular bipartite graphs in subexponential time when
![]() $d$
grows with the number of vertices of the instance. Our work is motivated in part by the question of whether a subexponential-time approximation algorithm for the Potts partition function can be found (at temperatures known to be #BIS-hard).
$d$
grows with the number of vertices of the instance. Our work is motivated in part by the question of whether a subexponential-time approximation algorithm for the Potts partition function can be found (at temperatures known to be #BIS-hard).
In general, the interaction between probabilistic phase transitions or thresholds such as
![]() $\beta _o$
and the computational complexity of approximating partition functions has received substantial attention. For example, while the (Gibbs uniqueness) phase transition on the infinite
$\beta _o$
and the computational complexity of approximating partition functions has received substantial attention. For example, while the (Gibbs uniqueness) phase transition on the infinite
![]() $d$
-regular tree corresponds to an NP-hardness threshold in graphs of maximum degree
$d$
-regular tree corresponds to an NP-hardness threshold in graphs of maximum degree
![]() $d$
for antiferromagnetic 2-spin models such as the hard-core model and the Ising model [Reference Sly37, Reference Sly and Sun39, Reference Galanis, Štefankovič and Vigoda18], for the ferromagnetic Potts model on the random
$d$
for antiferromagnetic 2-spin models such as the hard-core model and the Ising model [Reference Sly37, Reference Sly and Sun39, Reference Galanis, Štefankovič and Vigoda18], for the ferromagnetic Potts model on the random
![]() $d$
-regular graph neither the Gibbs uniqueness phase transition nor the order-disorder threshold correspond to a computational threshold [Reference Helmuth, Jenssen and Perkins21] when
$d$
-regular graph neither the Gibbs uniqueness phase transition nor the order-disorder threshold correspond to a computational threshold [Reference Helmuth, Jenssen and Perkins21] when
![]() $q$
is large enough in terms of
$q$
is large enough in terms of
![]() $d$
. The methods of [Reference Helmuth, Jenssen and Perkins21] rely on large
$d$
. The methods of [Reference Helmuth, Jenssen and Perkins21] rely on large
![]() $q$
, and our work addresses the question of how one can work with smaller
$q$
, and our work addresses the question of how one can work with smaller
![]() $q$
.
$q$
.
While our primary objective is to give algorithms for approximating
![]() $Z_G(q,\beta )$
in the #BIS-hardness region (i.e. low temperatures), we also investigate phase transitions subject to much weaker conditions than those satisfied by the random regular graph. To this end, we develop a high-temperature algorithm for general
$Z_G(q,\beta )$
in the #BIS-hardness region (i.e. low temperatures), we also investigate phase transitions subject to much weaker conditions than those satisfied by the random regular graph. To this end, we develop a high-temperature algorithm for general
![]() $d$
-regular instances that works up to some
$d$
-regular instances that works up to some
![]() $\beta _1(q,d)$
such that
$\beta _1(q,d)$
such that
![]() $\beta _1\sim \beta _o$
as
$\beta _1\sim \beta _o$
as
![]() $d\to \infty$
. Since the Gibbs uniqueness threshold is less than
$d\to \infty$
. Since the Gibbs uniqueness threshold is less than
![]() $\beta _o$
, our work gives a polynomial-time approximation algorithm in the Gibbs uniqueness region for regular graphs and does so for the largest-known range of
$\beta _o$
, our work gives a polynomial-time approximation algorithm in the Gibbs uniqueness region for regular graphs and does so for the largest-known range of
![]() $q$
.
$q$
.
1.1 Our results
Let
![]() $G = (V,E)$
be a
$G = (V,E)$
be a
![]() $d$
-regular graph on
$d$
-regular graph on
![]() $n$
vertices. For a set of vertices
$n$
vertices. For a set of vertices
![]() $A\subset V$
, let the edge-boundary
$A\subset V$
, let the edge-boundary
![]() $\nabla (A)$
of
$\nabla (A)$
of
![]() $A$
be the set of edges of
$A$
be the set of edges of
![]() $G$
with precisely one endpoint in
$G$
with precisely one endpoint in
![]() $A$
. For
$A$
. For
![]() $\eta \gt 0$
, we say that a graph
$\eta \gt 0$
, we say that a graph
![]() $G$
is an
$G$
is an
![]() $\eta$
-expander if
$\eta$
-expander if
We note here that the
![]() $d$
-dimensional hypercube
$d$
-dimensional hypercube
![]() $Q_d$
is a
$Q_d$
is a
![]() $1$
-expander, and that
$1$
-expander, and that
![]() $\eta$
-expansion differs by a factor
$\eta$
-expansion differs by a factor
![]() $d$
from the usual definition of edge expansion
$d$
from the usual definition of edge expansion
![]() $\phi$
in an
$\phi$
in an
![]() $n$
-vertex
$n$
-vertex
![]() $d$
-regular graph,
$d$
-regular graph,
![]() $\phi (G) = \min _{0 \lt |A| \le n/2}|\nabla (A)|/(d|A|)$
.
$\phi (G) = \min _{0 \lt |A| \le n/2}|\nabla (A)|/(d|A|)$
.
For
![]() $z\gt 0$
and
$z\gt 0$
and
![]() $\delta \in [0,1)$
, we say that
$\delta \in [0,1)$
, we say that
![]() $\hat z$
is a
$\hat z$
is a
![]() $\delta$
-relative approximation to
$\delta$
-relative approximation to
![]() $z$
if
$z$
if
![]() $1- \delta \le z/\hat z \le 1+\delta$
. For a given
$1- \delta \le z/\hat z \le 1+\delta$
. For a given
![]() $q \in \mathbb{N}$
and
$q \in \mathbb{N}$
and
![]() $\beta \gt 0$
, a fully polynomial-time approximation scheme (FPTAS) for
$\beta \gt 0$
, a fully polynomial-time approximation scheme (FPTAS) for
![]() $Z_G(q,\beta )$
is an algorithm that for every
$Z_G(q,\beta )$
is an algorithm that for every
![]() $\delta \gt 0$
outputs a
$\delta \gt 0$
outputs a
![]() $\delta$
-relative approximation to
$\delta$
-relative approximation to
![]() $Z_G(q,\beta )$
and runs in time polynomial in
$Z_G(q,\beta )$
and runs in time polynomial in
![]() $n$
and
$n$
and
![]() $1/\delta$
. A polynomial-time sampling scheme for
$1/\delta$
. A polynomial-time sampling scheme for
![]() $\mu _{G,q,\beta }$
outputs a random spin assignment with distribution
$\mu _{G,q,\beta }$
outputs a random spin assignment with distribution
![]() $\hat \mu$
that lies within
$\hat \mu$
that lies within
![]() $\delta$
total variation distance of
$\delta$
total variation distance of
![]() $\mu _{G,q,\beta }$
and runs in time polynomial in
$\mu _{G,q,\beta }$
and runs in time polynomial in
![]() $n$
and
$n$
and
![]() $1/\delta$
. Our main theorem is the following.
$1/\delta$
. Our main theorem is the following.
Theorem 1.
For every
![]() $\epsilon \gt 0$
, there exists
$\epsilon \gt 0$
, there exists
![]() $d_0(\epsilon )$
such that for
$d_0(\epsilon )$
such that for
![]() $d \ge d_0(\epsilon )$
,
$d \ge d_0(\epsilon )$
,
![]() $q \ge d^c$
where
$q \ge d^c$
where
![]() $c$
is an absolute constant, and positive
$c$
is an absolute constant, and positive
![]() $\beta \notin ((1-\epsilon )\beta _o, (1+\epsilon )\beta _o)$
, there exist
$\beta \notin ((1-\epsilon )\beta _o, (1+\epsilon )\beta _o)$
, there exist
-
(1) an FPTAS for
 $Z_G(q,\beta )$
, and
$Z_G(q,\beta )$
, and
-
(2) a polynomial-time sampling scheme for
 $\mu _{G,q,\beta }$
$\mu _{G,q,\beta }$
for
![]() $G$
in the class of
$G$
in the class of
![]() $d$
-regular
$d$
-regular
![]() $2$
-expander graphs, and for
$2$
-expander graphs, and for
![]() $G$
in the class of triangle-free
$G$
in the class of triangle-free
![]() $d$
-regular
$d$
-regular
![]() $1$
-expander graphs.
$1$
-expander graphs.
While the constants
![]() $2$
and
$2$
and
![]() $1$
marking the limit of our expansion range may seem arbitrary, they represent a subtle barrier in our proofs. All
$1$
marking the limit of our expansion range may seem arbitrary, they represent a subtle barrier in our proofs. All
![]() $n$
-vertex
$n$
-vertex
![]() $d$
-regular graphs that are
$d$
-regular graphs that are
![]() $2$
-expanders or triangle-free
$2$
-expanders or triangle-free
![]() $1$
-expanders must have min-cut
$1$
-expanders must have min-cut
![]() $d$
and the property that a set
$d$
and the property that a set
![]() $A$
with
$A$
with
![]() $2\le |A|\le n/2$
vertices on one side has edge-boundary at least
$2\le |A|\le n/2$
vertices on one side has edge-boundary at least
![]() $2d-2$
(see (7)). We choose not to pursue any additional case analysis and parameter trade-offs that might overcome this barrier. One option, as in [Reference Helmuth, Jenssen and Perkins21], is to require stronger (e.g.
$2d-2$
(see (7)). We choose not to pursue any additional case analysis and parameter trade-offs that might overcome this barrier. One option, as in [Reference Helmuth, Jenssen and Perkins21], is to require stronger (e.g.
![]() $\Omega (d)$
) expansion for small sets but we avoided this assumption for Theorem 1. It is also worth noting that we require
$\Omega (d)$
) expansion for small sets but we avoided this assumption for Theorem 1. It is also worth noting that we require
![]() $d_0(\epsilon ) \geq e^{\Omega (1/\epsilon )}$
.
$d_0(\epsilon ) \geq e^{\Omega (1/\epsilon )}$
.
In the low-temperature regime,
![]() $\beta \gt (1+\epsilon )\beta _o$
, this is a significant improvement over a previous result of Jenssen et al. [Reference Jenssen, Keevash and Perkins24] which required that
$\beta \gt (1+\epsilon )\beta _o$
, this is a significant improvement over a previous result of Jenssen et al. [Reference Jenssen, Keevash and Perkins24] which required that
![]() $q \geq d^{\Omega (d)}$
, as well as the graph being an
$q \geq d^{\Omega (d)}$
, as well as the graph being an
![]() $\Omega (d)$
-expander when considering the same range of temperatures. Briefly, the statement in [Reference Jenssen, Keevash and Perkins24] permits weaker
$\Omega (d)$
-expander when considering the same range of temperatures. Briefly, the statement in [Reference Jenssen, Keevash and Perkins24] permits weaker
![]() $\eta$
-expansion than
$\eta$
-expansion than
![]() $\eta =2$
, but at the cost of larger
$\eta =2$
, but at the cost of larger
![]() $\beta$
. We focusFootnote 1 on obtaining an algorithm that still applies when
$\beta$
. We focusFootnote 1 on obtaining an algorithm that still applies when
![]() $\beta$
is close to
$\beta$
is close to
![]() $\beta _o$
. For a
$\beta _o$
. For a
![]() $\delta$
-relative approximation, the high-temperature algorithm presented in Theorem 1 runs in time
$\delta$
-relative approximation, the high-temperature algorithm presented in Theorem 1 runs in time
![]() $\left (n/\delta \right )^{O_{\epsilon }(\ln d)}$
and the low-temperature algorithm runs in time
$\left (n/\delta \right )^{O_{\epsilon }(\ln d)}$
and the low-temperature algorithm runs in time
![]() $\left (n/\delta \right )^{O_{\epsilon }\left (d/\eta \right )}$
.
$\left (n/\delta \right )^{O_{\epsilon }\left (d/\eta \right )}$
.
For the high-temperature regime where
![]() $\beta \leq (1-\epsilon )\beta _o$
, an expansion assumption is not required and the
$\beta \leq (1-\epsilon )\beta _o$
, an expansion assumption is not required and the
![]() $d$
-regular condition can be relaxed to maximum degree
$d$
-regular condition can be relaxed to maximum degree
![]() $d$
. Moreover, there is a function
$d$
. Moreover, there is a function
![]() $q_0(\epsilon )$
such that our method only requires
$q_0(\epsilon )$
such that our method only requires
![]() $q\ge q_0(\epsilon )$
. In particular, this gives an FPTAS to sample in the uniqueness regime (and a bit beyond) for large enough
$q\ge q_0(\epsilon )$
. In particular, this gives an FPTAS to sample in the uniqueness regime (and a bit beyond) for large enough
![]() $q$
and
$q$
and
![]() $d$
. This improves upon ([Reference Borgs, Chayes, Helmuth, Perkins and Tetali2], Theorem 2.4) which gives an FPTAS in the range
$d$
. This improves upon ([Reference Borgs, Chayes, Helmuth, Perkins and Tetali2], Theorem 2.4) which gives an FPTAS in the range
![]() $\beta \le \frac{3}{2}\ln (q)/d$
for all
$\beta \le \frac{3}{2}\ln (q)/d$
for all
![]() $d\ge 2$
when
$d\ge 2$
when
![]() $q\ge \exp (\Omega (d\ln d))$
(see also a slightly different version in [8] that applies up to
$q\ge \exp (\Omega (d\ln d))$
(see also a slightly different version in [8] that applies up to
![]() $(1-\epsilon )\beta _o$
but requires
$(1-\epsilon )\beta _o$
but requires
![]() $q\ge \exp (\Omega (d^{3/2}\ln d))$
).
$q\ge \exp (\Omega (d^{3/2}\ln d))$
).
The ‘gap’ in allowed values of
![]() $\beta$
in Theorem 1 is partly due to our focus on reducing the necessary lower bound on
$\beta$
in Theorem 1 is partly due to our focus on reducing the necessary lower bound on
![]() $q$
. Such a gap should not be necessary (see [Reference Helmuth, Jenssen and Perkins21]) for large enough
$q$
. Such a gap should not be necessary (see [Reference Helmuth, Jenssen and Perkins21]) for large enough
![]() $q$
, and it would be interesting to close the gap without strengthening the lower bound on
$q$
, and it would be interesting to close the gap without strengthening the lower bound on
![]() $q$
in the statement.
$q$
in the statement.
Guided by results for other models in statistical physics, one might expect efficient approximation algorithms for
![]() $Z_G(q,\beta )$
to exist on graphs of maximum degree
$Z_G(q,\beta )$
to exist on graphs of maximum degree
![]() $d$
when
$d$
when
![]() $(q,\beta )$
lie in the Gibbs uniqueness region of the infinite
$(q,\beta )$
lie in the Gibbs uniqueness region of the infinite
![]() $d$
-regular tree, for any
$d$
-regular tree, for any
![]() $d,q\ge 3$
(For
$d,q\ge 3$
(For
![]() $d=2$
the model is exactly solvable and
$d=2$
the model is exactly solvable and
![]() $q=2$
gives the Ising model, which is rather well-understood by comparison). Our methods give an FPTAS in this region for the largest-known range of
$q=2$
gives the Ising model, which is rather well-understood by comparison). Our methods give an FPTAS in this region for the largest-known range of
![]() $d$
and
$d$
and
![]() $q$
.
$q$
.
Theorem 2.
There exist absolute constants
![]() $d'$
and
$d'$
and
![]() $q'$
such that for all
$q'$
such that for all
![]() $d\ge d'$
and
$d\ge d'$
and
![]() $q\ge q'$
, there is an FPTAS for
$q\ge q'$
, there is an FPTAS for
![]() $Z_G(q,\beta )$
on graphs of maximum degree
$Z_G(q,\beta )$
on graphs of maximum degree
![]() $d$
when
$d$
when
![]() $\beta \gt 0$
lies in the Gibbs uniqueness region of the
$\beta \gt 0$
lies in the Gibbs uniqueness region of the
![]() $q$
-color Potts model on the infinite
$q$
-color Potts model on the infinite
![]() $d$
-regular tree.
$d$
-regular tree.
While our high-temperature result does not require the same novel combinatorial techniques (described below) as the low-temperature improvement, our work as a whole emphasises some interesting aspects of the polymer models that we use to prove the above results. We discuss in a concluding section the ‘critical window’ where
![]() $\beta$
is close to
$\beta$
is close to
![]() $\beta _o$
and the difficulties associated with lowering
$\beta _o$
and the difficulties associated with lowering
![]() $q$
.
$q$
.
One of our key innovations for the low-temperature result, which is of independent interest, is an upper bound on the number of sets in a
![]() $d$
-regular
$d$
-regular
![]() $\eta$
-expander with a prescribed edge-boundary size
$\eta$
-expander with a prescribed edge-boundary size
![]() $b$
. This is reminiscent of container theorems from extremal graph theory that bound the number of independent sets in some graph or hypergraph. The origin of container theorems can be traced back to Kleitman and Winston [Reference Kleitman and Winston30, Reference Kleitman and Winston31] but the ideas were developed significantly by Sapozhenko [Reference Sapozhenko35, Reference Sapozhenko36], who specifically studied independent sets in expander graphs and the hypercube. Algorithmic applications of containers for counting independent sets in bipartite graphs were recently given by Jenssen and Perkins [Reference Jenssen and Perkins25], also with Potukuchi [Reference Jenssen, Perkins and Potukuchi26]. The type of bound we need does not seem to relate closely to an existing container theorem, and we prove the following novel result using ideas from randomised algorithms. We say that a subset
$b$
. This is reminiscent of container theorems from extremal graph theory that bound the number of independent sets in some graph or hypergraph. The origin of container theorems can be traced back to Kleitman and Winston [Reference Kleitman and Winston30, Reference Kleitman and Winston31] but the ideas were developed significantly by Sapozhenko [Reference Sapozhenko35, Reference Sapozhenko36], who specifically studied independent sets in expander graphs and the hypercube. Algorithmic applications of containers for counting independent sets in bipartite graphs were recently given by Jenssen and Perkins [Reference Jenssen and Perkins25], also with Potukuchi [Reference Jenssen, Perkins and Potukuchi26]. The type of bound we need does not seem to relate closely to an existing container theorem, and we prove the following novel result using ideas from randomised algorithms. We say that a subset
![]() $A$
of vertices in a graph
$A$
of vertices in a graph
![]() $G$
is connected if the induced subgraph
$G$
is connected if the induced subgraph
![]() $G[A]$
is connected.
$G[A]$
is connected.
Theorem 3.
Let
![]() $G=(V,E)$
be a
$G=(V,E)$
be a
![]() $d$
-regular
$d$
-regular
![]() $\eta$
-expander and let
$\eta$
-expander and let
![]() $u$
be a vertex in
$u$
be a vertex in
![]() $G$
. Then the number of connected sets
$G$
. Then the number of connected sets
![]() $A\subset V$
of size at most
$A\subset V$
of size at most
![]() $|V|/2$
such that
$|V|/2$
such that
![]() $u \in A$
and
$u \in A$
and
![]() $|\nabla (A)|=b$
is at most
$|\nabla (A)|=b$
is at most
![]() $d^{O\left ((1+1/\eta )b/d\right )}$
.
$d^{O\left ((1+1/\eta )b/d\right )}$
.
One way of interpreting the theorem is that we show that a large-girth graph (or, if you prefer, an infinite regular tree) is extremal for the number of connected sets with a given boundary
![]() $b$
, we explain this heuristic in the overview below.
$b$
, we explain this heuristic in the overview below.
Our methods also give an idea of the typical structure of the Potts model on
![]() $\eta$
-expanders below and above the order-disorder threshold
$\eta$
-expanders below and above the order-disorder threshold
![]() $\beta _o$
. More precisely, we show the following.
$\beta _o$
. More precisely, we show the following.
Theorem 4.
Let
![]() $\epsilon$
,
$\epsilon$
,
![]() $d$
,
$d$
,
![]() $q$
, and
$q$
, and
![]() $G$
be as in Theorem 1, with
$G$
be as in Theorem 1, with
![]() $n=|V(G)|$
. As
$n=|V(G)|$
. As
![]() $n\to \infty$
, for a colouring sampled from the ferromagnetic Potts model,
$n\to \infty$
, for a colouring sampled from the ferromagnetic Potts model,
-
(1) for
 $\beta \lt (1 - \epsilon )\beta _o$
, each colour class has size
$\beta \lt (1 - \epsilon )\beta _o$
, each colour class has size
 $(1 + o(1))n/q$
with high probability, and
$(1 + o(1))n/q$
with high probability, and
-
(2) for
 $\beta \gt (1+\epsilon )\beta _o$
, there is a colour class that contains at least
$\beta \gt (1+\epsilon )\beta _o$
, there is a colour class that contains at least
 $(1-o_d(1))n$
vertices with high probability.
$(1-o_d(1))n$
vertices with high probability.
The main result of [Reference Helmuth, Jenssen and Perkins21] gives a much more complete description of Potts model (in fact, the more general random cluster model that we describe below) on
![]() $d$
-regular locally tree-like graphs subject to an
$d$
-regular locally tree-like graphs subject to an
![]() $\eta$
-expansion condition of the form
$\eta$
-expansion condition of the form
![]() $\eta =\Omega (d)$
and a stronger small-set expansion condition. It would be interesting to increase the precision of our approach to give a similar description subject to weaker conditions, e.g. for the Potts model on the hypercube. We give an example of what our methods currently reveal about the Potts model on the hypercube below.
$\eta =\Omega (d)$
and a stronger small-set expansion condition. It would be interesting to increase the precision of our approach to give a similar description subject to weaker conditions, e.g. for the Potts model on the hypercube. We give an example of what our methods currently reveal about the Potts model on the hypercube below.
An equivalent definition of
![]() $Z$
is given by the Fortuin–Kasteleyn representation [Reference Fortuin and Kasteleyn13]
$Z$
is given by the Fortuin–Kasteleyn representation [Reference Fortuin and Kasteleyn13]
where
![]() $c(A)$
is the number of connected components of the graph
$c(A)$
is the number of connected components of the graph
![]() $(V,A)$
on the same vertex set as
$(V,A)$
on the same vertex set as
![]() $G$
but with edge set
$G$
but with edge set
![]() $A$
. In this form,
$A$
. In this form,
![]() $Z$
is known as the partition function of the random cluster model, and it is easy to see that
$Z$
is known as the partition function of the random cluster model, and it is easy to see that
![]() $Z$
is a reparametrization of the Tutte polynomial of
$Z$
is a reparametrization of the Tutte polynomial of
![]() $G$
. The random cluster model is a distribution on subsets of edges where the probability mass of
$G$
. The random cluster model is a distribution on subsets of edges where the probability mass of
![]() $A \subseteq E$
is proportional to
$A \subseteq E$
is proportional to
![]() $q^{c(A)} (e^\beta - 1)^{|A|}$
. It is standard to change parameters via
$q^{c(A)} (e^\beta - 1)^{|A|}$
. It is standard to change parameters via
![]() $p=e^\beta -1$
. As an illustration of the power of our new techniques, we give the following structural result for the components induced by an edge set drawn from the random cluster model on the discrete
$p=e^\beta -1$
. As an illustration of the power of our new techniques, we give the following structural result for the components induced by an edge set drawn from the random cluster model on the discrete
![]() $d$
-dimensional hypercube
$d$
-dimensional hypercube
![]() $Q_d$
.
$Q_d$
.
Theorem 5.
Let
![]() $\epsilon \gt 0$
and
$\epsilon \gt 0$
and
![]() $d\ge d_0(\epsilon )$
for the
$d\ge d_0(\epsilon )$
for the
![]() $d_0$
in Theorem 1. For a constant
$d_0$
in Theorem 1. For a constant
![]() $c$
at least the minimum
$c$
at least the minimum
![]() $c$
of Theorem 1, let
$c$
of Theorem 1, let
![]() $q = d^{c}$
be a positive integer. There is a sequence
$q = d^{c}$
be a positive integer. There is a sequence
![]() $p_o = p_o(d,q)$
such that in the random cluster model on the
$p_o = p_o(d,q)$
such that in the random cluster model on the
![]() $d$
-regular discrete hypercube
$d$
-regular discrete hypercube
![]() $Q_d$
, for every
$Q_d$
, for every
![]() $\epsilon \gt 0$
,
$\epsilon \gt 0$
,
-
(1) when
 $p \leq (1 - \epsilon )p_o$
, every component has size at most
$p \leq (1 - \epsilon )p_o$
, every component has size at most
 $d$
with high probability, and
$d$
with high probability, and
-
(2) when
 $p \geq (1 + \epsilon )p_o$
, there is a unique connected component of size
$p \geq (1 + \epsilon )p_o$
, there is a unique connected component of size
 $2^d\left (1 - o(1)\right )$
with high probability.
$2^d\left (1 - o(1)\right )$
with high probability.
Some remarks are in order here. First, the condition
![]() $q = d^c$
means that the number of colours grows (poly-logarithmically) with the number of vertices in the graph. This is admittedly a slightly different regime than the more common one where
$q = d^c$
means that the number of colours grows (poly-logarithmically) with the number of vertices in the graph. This is admittedly a slightly different regime than the more common one where
![]() $q$
and
$q$
and
![]() $d$
are both fixed. This difference turns out to be inconsequential, and the behaviour predicted by Theorem 4 ultimately holds.
$d$
are both fixed. This difference turns out to be inconsequential, and the behaviour predicted by Theorem 4 ultimately holds.
Second, we note that for any constant
![]() $c\gt 0$
and
$c\gt 0$
and
![]() $q=d^c$
,
$q=d^c$
,
![]() $\ln (1 + p_o) \sim p_o \sim \frac{2\ln q}{d}$
as
$\ln (1 + p_o) \sim p_o \sim \frac{2\ln q}{d}$
as
![]() $d\to \infty$
. When considering the random cluster model one should not need to restrict
$d\to \infty$
. When considering the random cluster model one should not need to restrict
![]() $q$
to the positive integers, though our methods currently require the condition that
$q$
to the positive integers, though our methods currently require the condition that
![]() $q$
is an integer. It would be interesting to remove this restriction, and we discuss the barriers in the concluding section.
$q$
is an integer. It would be interesting to remove this restriction, and we discuss the barriers in the concluding section.
1.2 An overview of techniques
Our algorithms follow from the cluster expansion for abstract polymer models, which was first used to design sampling algorithms for the Potts model by Helmuth et al. [Reference Helmuth, Perkins and Regts23]. The method has been studied intensively since, including further works concerning the ferromagnetic Potts model [Reference Jenssen, Keevash and Perkins24, Reference Borgs, Chayes, Helmuth, Perkins and Tetali2, Reference Helmuth, Jenssen and Perkins21] and many other works tackling various Markov random fields. At a high level, the method proceeds by transforming the partition function into a representation that corresponds to an abstract but particularly well-studied polymer model from statistical mechanics. The strength of this approach lies in the fact that general conditions on these models give a wealth of probabilistic and algorithmic information. The specific polymer models we rely on have appeared in several earlier works [Reference Jenssen, Keevash and Perkins24, Reference Borgs, Chayes, Helmuth, Perkins and Tetali2, Reference Helmuth, Jenssen and Perkins21, 8, Reference Carlson, Davies and Kolla7], and our key innovations are improved analyses of the models to obtain algorithms under significantly weaker assumptions. Let us split the rest of the discussion into the low-temperature regime (
![]() $\beta \geq (1 +\epsilon )\beta _o$
) and the high-temperature regime (
$\beta \geq (1 +\epsilon )\beta _o$
) and the high-temperature regime (
![]() $\beta \leq (1 -\epsilon )\beta _o$
).
$\beta \leq (1 -\epsilon )\beta _o$
).
Low temperature. This part contains our main contributions. Some of the difficulties we face boil down to understanding certain combinatorial questions that are of independent interest. Informally, two problems that arise are as follows. Let
![]() $G$
be a
$G$
be a
![]() $d$
-regular
$d$
-regular
![]() $\eta$
-expander with
$\eta$
-expander with
![]() $n$
vertices.
$n$
vertices.
-
(a) What is the number of connected, induced subgraphs of
 $G$
containing a given vertex and with an edge-boundary of size
$G$
containing a given vertex and with an edge-boundary of size
 $b$
?
$b$
? -
(b) What is the number of
 $q$
-colorings of
$q$
-colorings of
 $G$
that have exactly
$G$
that have exactly
 $k$
non-monochromatic edges?
$k$
non-monochromatic edges?
Let us first quantitatively motivate the types of answers that can be expected for these questions. For (a), suppose that
![]() $G$
is weakly ‘locally tree-like’ in the sense that every connected set of
$G$
is weakly ‘locally tree-like’ in the sense that every connected set of
![]() $a \ll n$
vertices spans
$a \ll n$
vertices spans
![]() $O(a)$
edges and therefore has an edge-boundary of size
$O(a)$
edges and therefore has an edge-boundary of size
![]() $\Omega (d a)$
. Working backwards, a naive heuristic is that a typical connected subset of
$\Omega (d a)$
. Working backwards, a naive heuristic is that a typical connected subset of
![]() $\Theta (b/d)$
vertices has an edge-boundary of size
$\Theta (b/d)$
vertices has an edge-boundary of size
![]() $b$
. The locally tree-like property also means that the number of connected, induced subgraphs of
$b$
. The locally tree-like property also means that the number of connected, induced subgraphs of
![]() $G$
containing a given vertex is roughly the number of trees with degree at most
$G$
containing a given vertex is roughly the number of trees with degree at most
![]() $d$
rooted at the vertex, and hence for subgraphs on
$d$
rooted at the vertex, and hence for subgraphs on
![]() $\Theta (b/d)$
vertices this number is roughly
$\Theta (b/d)$
vertices this number is roughly
![]() $d^{O(b/d)}$
, we can answer (a) for locally tree-like graphs. The same argument also works for graphs satisfying condition (3) (by noting that a set of boundary size
$d^{O(b/d)}$
, we can answer (a) for locally tree-like graphs. The same argument also works for graphs satisfying condition (3) (by noting that a set of boundary size
![]() $b$
may have at most
$b$
may have at most
![]() $b/\eta$
vertices) to give a bound of
$b/\eta$
vertices) to give a bound of
![]() $d^{O(b/\eta )}$
. Theorem 3 gives a stronger upper bound for graphs satisfying our expansion condition (3) by finding a small ‘certificate’ for each connected, induced subgraph with a prescribed edge-boundary size. Since the certificate is small, there cannot be too many valid certificates and an upper bound on the number of sets we are interested in follows. One of the key tools for the proof is a standard but elegant adaptation of Karger’s randomised algorithm for finding minimum cuts [Reference Karger27] to the problem of counting cuts; see Theorem 13. To the best of our knowledge, our application of this celebrated result in combinatorial optimisation to analyse a counting algorithm is novel, and the technique may be of independent interest. Some additional ideas used in the proof can be found in [Reference Potukuchi and Yepremyan34].
$d^{O(b/\eta )}$
. Theorem 3 gives a stronger upper bound for graphs satisfying our expansion condition (3) by finding a small ‘certificate’ for each connected, induced subgraph with a prescribed edge-boundary size. Since the certificate is small, there cannot be too many valid certificates and an upper bound on the number of sets we are interested in follows. One of the key tools for the proof is a standard but elegant adaptation of Karger’s randomised algorithm for finding minimum cuts [Reference Karger27] to the problem of counting cuts; see Theorem 13. To the best of our knowledge, our application of this celebrated result in combinatorial optimisation to analyse a counting algorithm is novel, and the technique may be of independent interest. Some additional ideas used in the proof can be found in [Reference Potukuchi and Yepremyan34].
For (b), the heuristic is as follows: the simplest way that one can obtain a
![]() $q$
-coloring of
$q$
-coloring of
![]() $G$
with
$G$
with
![]() $k$
non-monochromatic edges is by colouring all but
$k$
non-monochromatic edges is by colouring all but
![]() $k/d$
randomly chosen vertices, which for small
$k/d$
randomly chosen vertices, which for small
![]() $k$
are likely to form an independent set, in the same colour. The independent set on
$k$
are likely to form an independent set, in the same colour. The independent set on
![]() $k/d$
vertices can be coloured arbitrarily with the other colors, giving the required
$k/d$
vertices can be coloured arbitrarily with the other colors, giving the required
![]() $k$
non-monochromatic edges. This gives a lower bound of roughly
$k$
non-monochromatic edges. This gives a lower bound of roughly
![]() $\binom{n}{k/d} q^{k/d} = (ndq/k)^{\Omega (k/d)}$
. We provide another enumeration result (Lemma 16) that again justifies this heuristic for graphs satisfying the expansion condition (3). Note that the emergence of problem (b) involving colourings means that it is not straightforward to generalise our low-temperature algorithm to the random cluster model (with non-integer
$\binom{n}{k/d} q^{k/d} = (ndq/k)^{\Omega (k/d)}$
. We provide another enumeration result (Lemma 16) that again justifies this heuristic for graphs satisfying the expansion condition (3). Note that the emergence of problem (b) involving colourings means that it is not straightforward to generalise our low-temperature algorithm to the random cluster model (with non-integer
![]() $q$
).
$q$
).
In a calculation establishing that the polymer models we use provide efficient algorithms, we require upper bounds on
![]() $Z_\gamma (q-1,\beta )$
where
$Z_\gamma (q-1,\beta )$
where
![]() $\gamma$
is a connected, induced subgraph of
$\gamma$
is a connected, induced subgraph of
![]() $G$
. Previous works used crude bounds here, and we use better bounds from [Reference Sah, Sawhney, Stoner and Zhao40] that are tight when
$G$
. Previous works used crude bounds here, and we use better bounds from [Reference Sah, Sawhney, Stoner and Zhao40] that are tight when
![]() $\gamma$
is isomorphic to
$\gamma$
is isomorphic to
![]() $K_{d+1}$
, or in the triangle-free case, complete bipartite graphs
$K_{d+1}$
, or in the triangle-free case, complete bipartite graphs
![]() $K_{d,d}$
. This is still not ideal as an
$K_{d,d}$
. This is still not ideal as an
![]() $\eta$
-expander cannot contain such subgraphs, but it is generally difficult to prove improved bounds, or even identify graph properties that would allow an improved bound in such problems [Reference Potukuchi and Yepremyan34]. This is another place in which our methods require the Potts model, as such bounds are not known for the random cluster model. In this way, our algorithmic work motivates new questions in extremal graph theory; see Conjectures 25 and 26.
$\eta$
-expander cannot contain such subgraphs, but it is generally difficult to prove improved bounds, or even identify graph properties that would allow an improved bound in such problems [Reference Potukuchi and Yepremyan34]. This is another place in which our methods require the Potts model, as such bounds are not known for the random cluster model. In this way, our algorithmic work motivates new questions in extremal graph theory; see Conjectures 25 and 26.
High temperature. The main idea to handle this regime is to switch to the random cluster model. The primary reason for this is to access a convenient representation as a polymer model. Using the Edwards–Sokal coupling [Reference Edwards and Sokal12], one can view both of these models on the same probability space. The coupling gives an algorithm for converting a random cluster sampling algorithm to a Potts model sampling algorithm and vice versa. The polymer model we use was also generalised to a partition function related to Unique Games in [8]. The analysis given in this paper improves upon the analyses in [Reference Borgs, Chayes, Helmuth, Perkins and Tetali2] and [8]. Moreover, this part of the proof works for any graph of maximum degree
![]() $d$
(i.e. we can dispense with
$d$
(i.e. we can dispense with
![]() $d$
-regularity and with an expansion assumption), a fact present in these earlier works which does not seem to be well-known in general.
$d$
-regularity and with an expansion assumption), a fact present in these earlier works which does not seem to be well-known in general.
1.3 Related work
Algorithmic applications of the cluster expansion originate in [Reference Helmuth, Perkins and Regts23], and for the ferromagnetic Potts model in particular there are two works of note that establish algorithms at all temperatures on subgraphs of the integer lattice
![]() $\mathbb{Z}^d$
[Reference Borgs, Chayes, Helmuth, Perkins and Tetali2] and on regular graphs with strong expansion [Reference Helmuth, Jenssen and Perkins21]. These results rely on
$\mathbb{Z}^d$
[Reference Borgs, Chayes, Helmuth, Perkins and Tetali2] and on regular graphs with strong expansion [Reference Helmuth, Jenssen and Perkins21]. These results rely on
![]() $q$
being at least exponentially large in
$q$
being at least exponentially large in
![]() $d$
(and even larger if the expansion guarantee is as weak as that of Theorem 1), which is a substantial drawback but in return the approaches work for all temperatures. The focus of our work is slightly different, and essentially we pay for working with smaller
$d$
(and even larger if the expansion guarantee is as weak as that of Theorem 1), which is a substantial drawback but in return the approaches work for all temperatures. The focus of our work is slightly different, and essentially we pay for working with smaller
![]() $q$
that grows only polynomially with
$q$
that grows only polynomially with
![]() $d$
(along with much weaker expansion) by accepting a small gap in our techniques around the threshold
$d$
(along with much weaker expansion) by accepting a small gap in our techniques around the threshold
![]() $\beta _o$
.
$\beta _o$
.
Our main tool is the cluster expansion for abstract polymer models, as in [Reference Helmuth, Perkins and Regts23, Reference Jenssen, Keevash and Perkins24, Reference Borgs, Chayes, Helmuth, Perkins and Tetali2, Reference Helmuth, Jenssen and Perkins21] (and many more works), where deterministic approximation algorithms for partition functions follow from convergent cluster expansions by approximating a truncated series. See also Barvinok’s work (e.g. the monograph [Reference Barvinok1]) which follows a similar series approximation approach. A twist on the cluster expansion method originating in [Reference Chen, Galanis, Goldberg, Perkins, Stewart and Vigoda9] uses a Markov chain to sample from an abstract polymer model. The approaches of [Reference Jenssen, Keevash and Perkins24, Reference Chen, Galanis, Goldberg, Perkins, Stewart and Vigoda9] were combined and generalised in [Reference Galanis, Goldberg and Stewart14] to give algorithms for general spin systems on bipartite expanders. We do not pursue Markov-chain-based sampling from polymer models here as the conditions required in [Reference Chen, Galanis, Goldberg, Perkins, Stewart and Vigoda9, Reference Galanis, Goldberg and Stewart14, Reference Blanca, Cannon and Perkins3] (i.e. upper bounds on polymer weights) are stronger than what we can guarantee with our current methods, and we do not want to restrict our attention to bipartite graphs.
A popular approach to approximate counting and sampling is to simulate a Markov chain whose stationary distribution is the Gibbs measure of interest. For the Potts model there are two main Markov chains, the Glauber dynamics and the Swendsen–Wang dynamics. The main result of [Reference Bordewich, Greenhill and Patel6] shows for graphs of maximum degree
![]() $d$
that Glauber dynamics is rapidly mixing for
$d$
that Glauber dynamics is rapidly mixing for
![]() $\beta$
up to a certain threshold and slow mixing for
$\beta$
up to a certain threshold and slow mixing for
![]() $\beta$
at least some slightly larger threshold. For Glauber dynamics on the random regular graph there is an improved understanding: the Gibbs uniqueness threshold marks the change from rapid mixing to torpid mixing [Reference Blanca and Gheissari4, Reference Coja-Oghlan, Galanis, Goldberg, Ravelomanana, Stefankovic and Vigoda10]. For comparison with our results, we note that each of the three thresholds discussed above lie below
$\beta$
at least some slightly larger threshold. For Glauber dynamics on the random regular graph there is an improved understanding: the Gibbs uniqueness threshold marks the change from rapid mixing to torpid mixing [Reference Blanca and Gheissari4, Reference Coja-Oghlan, Galanis, Goldberg, Ravelomanana, Stefankovic and Vigoda10]. For comparison with our results, we note that each of the three thresholds discussed above lie below
![]() $\beta _o$
and are asymptotic to
$\beta _o$
and are asymptotic to
![]() $\ln (q)/d$
as
$\ln (q)/d$
as
![]() $d\to \infty$
(which is asymptotically half of
$d\to \infty$
(which is asymptotically half of
![]() $\beta _o\sim 2\ln (q)/d$
as
$\beta _o\sim 2\ln (q)/d$
as
![]() $d\to \infty$
). It should be noted though, that these results hold for every
$d\to \infty$
). It should be noted though, that these results hold for every
![]() $q$
, while the results in this paper are restricted to large
$q$
, while the results in this paper are restricted to large
![]() $q$
. The picture for Swendsen–Wang dynamics on the random regular graph is less well-understood; see [Reference Coja-Oghlan, Galanis, Goldberg, Ravelomanana, Stefankovic and Vigoda10] and the references therein for details. An alternative approach to sampling from the ferromagnetic Potts model (and random cluster model) on the random regular graph in the Gibbs uniqueness regime of the ferromagnetic Potts model was given in [Reference Blanca, Galanis, Goldberg, Štefankovič, Vigoda and Yang5].
$q$
. The picture for Swendsen–Wang dynamics on the random regular graph is less well-understood; see [Reference Coja-Oghlan, Galanis, Goldberg, Ravelomanana, Stefankovic and Vigoda10] and the references therein for details. An alternative approach to sampling from the ferromagnetic Potts model (and random cluster model) on the random regular graph in the Gibbs uniqueness regime of the ferromagnetic Potts model was given in [Reference Blanca, Galanis, Goldberg, Štefankovič, Vigoda and Yang5].
1.4 organization
Section 2 is an introduction to abstract polymer models and their use in obtaining approximate counting and sampling algorithms. In Section 3 we prove our algorithmic result – Theorem 1– for the low-temperature case (
![]() $\beta \gt (1 + \epsilon )\beta _o$
) using the solutions to problems (a), (b), and extremal results on partition functions (Theorem 3, Lemma 8, and Lemmas 11 and 12 respectively). Section 4.1 is dedicated to the proof of our container-like result Theorem 3, solving problem (a); and Section 4.2 to the proof of Lemma 8, solving problem (b). In Section 5, we prove the extremal results, Lemmas 11 and 12. Section 6 consists of the proof of the high-temperature case (
$\beta \gt (1 + \epsilon )\beta _o$
) using the solutions to problems (a), (b), and extremal results on partition functions (Theorem 3, Lemma 8, and Lemmas 11 and 12 respectively). Section 4.1 is dedicated to the proof of our container-like result Theorem 3, solving problem (a); and Section 4.2 to the proof of Lemma 8, solving problem (b). In Section 5, we prove the extremal results, Lemmas 11 and 12. Section 6 consists of the proof of the high-temperature case (
![]() $\beta \lt (1-\epsilon )\beta _o$
) in Theorem 1. In Section 7 we use our results to characterise the structure of the Potts model, proving Theorem 4. Finally, Section 8 is dedicated to the structure of the random cluster model on the hypercube, namely the proof of Theorem 5. We conclude with a discussion of further directions to pursue.
$\beta \lt (1-\epsilon )\beta _o$
) in Theorem 1. In Section 7 we use our results to characterise the structure of the Potts model, proving Theorem 4. Finally, Section 8 is dedicated to the structure of the random cluster model on the hypercube, namely the proof of Theorem 5. We conclude with a discussion of further directions to pursue.
2. Preliminaries
2.1 Abstract polymer models
An abstract polymer model [Reference Gruber and Kunz17] is given by a set
![]() $\mathcal{P}$
of polymers, a compatibility relation
$\mathcal{P}$
of polymers, a compatibility relation
![]() $\sim$
on polymers, and a weight
$\sim$
on polymers, and a weight
![]() $w_\gamma$
associated to each polymer
$w_\gamma$
associated to each polymer
![]() $\gamma \in \mathcal{P}$
. In applications, polymers might be combinatorial objects such as vertex subsets or connected subgraphs of a graph. Let
$\gamma \in \mathcal{P}$
. In applications, polymers might be combinatorial objects such as vertex subsets or connected subgraphs of a graph. Let
![]() $\Omega$
denote the collection of all sets of pairwise compatible polymers, including the empty set (i.e. the set of independent sets in the graph on
$\Omega$
denote the collection of all sets of pairwise compatible polymers, including the empty set (i.e. the set of independent sets in the graph on
![]() $\mathcal{P}$
with edges between incompatible polymers). Then the polymer model partition function is
$\mathcal{P}$
with edges between incompatible polymers). Then the polymer model partition function is
The associated Gibbs measure
![]() $\nu$
on
$\nu$
on
![]() $\Omega$
is given by
$\Omega$
is given by
![]() $\nu (\Lambda ) = \prod _{\gamma \in \Lambda }w_\gamma/ \Xi$
, in much the same way as the Gibbs measures associated to the partition function of the Potts and random cluster models. It may be helpful to observe that
$\nu (\Lambda ) = \prod _{\gamma \in \Lambda }w_\gamma/ \Xi$
, in much the same way as the Gibbs measures associated to the partition function of the Potts and random cluster models. It may be helpful to observe that
![]() $\Xi$
is the multivariate independence polynomial of the graph on
$\Xi$
is the multivariate independence polynomial of the graph on
![]() $\mathcal{P}$
with edges between incompatible polymers, evaluated at the polymer weights given by
$\mathcal{P}$
with edges between incompatible polymers, evaluated at the polymer weights given by
![]() $w$
, and hence
$w$
, and hence
![]() $\nu$
is the associated hard-core measure.
$\nu$
is the associated hard-core measure.
The cluster expansion of
![]() $\Xi$
is a formal power series for
$\Xi$
is a formal power series for
![]() $\ln \Xi$
with terms given by clusters. A cluster
$\ln \Xi$
with terms given by clusters. A cluster
![]() $\Gamma$
is an ordered tuple of polymers, and to each
$\Gamma$
is an ordered tuple of polymers, and to each
![]() $\Gamma$
we associate an incompatibility graph
$\Gamma$
we associate an incompatibility graph
![]() $H(\Gamma )$
. This graph has vertex set
$H(\Gamma )$
. This graph has vertex set
![]() $\Gamma$
(i.e. a vertex for each polymer present in
$\Gamma$
(i.e. a vertex for each polymer present in
![]() $\Gamma$
with multiplicity) and each pair of vertices representing incompatible polymers is an edge of
$\Gamma$
with multiplicity) and each pair of vertices representing incompatible polymers is an edge of
![]() $H(\Gamma )$
. By convention, a polymer is incompatible with itself. We write
$H(\Gamma )$
. By convention, a polymer is incompatible with itself. We write
![]() $\mathcal{C}$
for the set of all clusters. The formal power series corresponding to the cluster expansion is then
$\mathcal{C}$
for the set of all clusters. The formal power series corresponding to the cluster expansion is then
where
![]() $\phi$
is the Ursell function
$\phi$
is the Ursell function
 \begin{equation*} \phi (\Gamma ) = \sum _{\substack {F\subset E(H(\Gamma )) \\ (V(H(\Gamma )), F) \text { connected}}} (-1)^{|F|}. \end{equation*}
\begin{equation*} \phi (\Gamma ) = \sum _{\substack {F\subset E(H(\Gamma )) \\ (V(H(\Gamma )), F) \text { connected}}} (-1)^{|F|}. \end{equation*}
We remark that for any polymer
![]() $\gamma$
, the tuples
$\gamma$
, the tuples
![]() $(\gamma ),(\gamma, \gamma ),\dotsc$
are valid clusters, and so the cluster expansion is an infinite sum. We use the following theorem to establish convergence and an important tail bound.
$(\gamma ),(\gamma, \gamma ),\dotsc$
are valid clusters, and so the cluster expansion is an infinite sum. We use the following theorem to establish convergence and an important tail bound.
Theorem 6 (Kotecký–Preiss [Reference Kotecký and Preiss29]). If there exist functions
![]() $f\,{:}\, \mathcal{P} \to [0, \infty )$
and
$f\,{:}\, \mathcal{P} \to [0, \infty )$
and
![]() $g\,{:}\, \mathcal{P} \to [0, \infty )$
such that for all
$g\,{:}\, \mathcal{P} \to [0, \infty )$
such that for all
![]() $\gamma \in \mathcal{P}$
,
$\gamma \in \mathcal{P}$
,
then the cluster expansion converges absolutely. Moreover, if we let
![]() $g(\Gamma )=\sum _{\gamma \in \Gamma }g(\gamma )$
, then for every polymer
$g(\Gamma )=\sum _{\gamma \in \Gamma }g(\gamma )$
, then for every polymer
![]() $\gamma$
,
$\gamma$
,
 \begin{equation} \sum _{\substack{\Gamma \in \mathcal{C}\\ \Gamma \not \sim \gamma }}\left |\phi (\Gamma )\prod _{\gamma^{\prime} \in \Gamma }w_{\gamma^{\prime}}\right | e^{g(\Gamma )} \leq f(\gamma ), \end{equation}
\begin{equation} \sum _{\substack{\Gamma \in \mathcal{C}\\ \Gamma \not \sim \gamma }}\left |\phi (\Gamma )\prod _{\gamma^{\prime} \in \Gamma }w_{\gamma^{\prime}}\right | e^{g(\Gamma )} \leq f(\gamma ), \end{equation}
where we write
![]() $\Gamma \not \sim \gamma$
to mean that the cluster
$\Gamma \not \sim \gamma$
to mean that the cluster
![]() $\Gamma$
contains a polymer that is incompatible with
$\Gamma$
contains a polymer that is incompatible with
![]() $\gamma$
.
$\gamma$
.
2.2 Algorithms from convergent cluster expansions
Approximate counting and sampling algorithms for polymer models follow from Theorem 6 in a rather standard way due to [Reference Helmuth, Perkins and Regts23] and subsequent works. In this paper we consider two polymer models that we define for an
![]() $n$
-vertex,
$n$
-vertex,
![]() $d$
-regular graph
$d$
-regular graph
![]() $G$
, and then we consider approximating
$G$
, and then we consider approximating
![]() $\Xi$
or approximately sampling from
$\Xi$
or approximately sampling from
![]() $\nu$
with time complexities measured in terms of
$\nu$
with time complexities measured in terms of
![]() $n$
and a desired approximation error
$n$
and a desired approximation error
![]() $\delta$
.
$\delta$
.
For a polymer model as above, let
![]() $g\,{:}\,\mathcal{P}\to [0,\infty )$
be as in Theorem 6, and extend
$g\,{:}\,\mathcal{P}\to [0,\infty )$
be as in Theorem 6, and extend
![]() $g$
to clusters
$g$
to clusters
![]() $\Gamma \in{\mathcal{C}}$
by
$\Gamma \in{\mathcal{C}}$
by
![]() $g(\Gamma ) = \sum _{\gamma \in \Gamma }g(\gamma )$
. An FPTAS for
$g(\Gamma ) = \sum _{\gamma \in \Gamma }g(\gamma )$
. An FPTAS for
![]() $\Xi$
follows from a few steps that one must check can be done efficiently:
$\Xi$
follows from a few steps that one must check can be done efficiently:
-
(1) Use (6) to show that there exists some
 $L= L(\epsilon )$
such thatis a close enough relative approximation of
$L= L(\epsilon )$
such thatis a close enough relative approximation of \begin{equation*} \Xi (L)\,{:\!=}\,\exp \left (\sum _{\substack {\Gamma \in {\mathcal {C}}\\ g(\Gamma ) \le L}}\phi (\Gamma )\prod _{\gamma \in \Gamma }w_\gamma \right ) \end{equation*}
\begin{equation*} \Xi (L)\,{:\!=}\,\exp \left (\sum _{\substack {\Gamma \in {\mathcal {C}}\\ g(\Gamma ) \le L}}\phi (\Gamma )\prod _{\gamma \in \Gamma }w_\gamma \right ) \end{equation*}
 $\Xi$
.
$\Xi$
.
-
(2) List all clusters
 $\Gamma \in{\mathcal{C}}$
such that
$\Gamma \in{\mathcal{C}}$
such that
 $g(\Gamma ) \le L$
.
$g(\Gamma ) \le L$
. -
(3) For each such cluster
 $\Gamma$
, compute
$\Gamma$
, compute
 $\phi (\Gamma )$
and
$\phi (\Gamma )$
and
 $\prod _{\gamma \in \Gamma } w_\gamma$
.
$\prod _{\gamma \in \Gamma } w_\gamma$
. -
(4) Compute
 $\Xi (L)$
directly from the above quantities.
$\Xi (L)$
directly from the above quantities.
The running time of this algorithm depends on
![]() $L$
, the definition of ‘close enough’, the time complexity of listing clusters and of computing polymer weights,
$L$
, the definition of ‘close enough’, the time complexity of listing clusters and of computing polymer weights,
![]() $\phi$
and
$\phi$
and
![]() $g$
. It has been established [Reference Helmuth, Perkins and Regts23, Reference Jenssen, Keevash and Perkins24, Reference Borgs, Chayes, Helmuth, Perkins and Tetali2] that for the polymer models we consider, the above steps can be carried out sufficiently fast for the definition of an FPTAS.
$g$
. It has been established [Reference Helmuth, Perkins and Regts23, Reference Jenssen, Keevash and Perkins24, Reference Borgs, Chayes, Helmuth, Perkins and Tetali2] that for the polymer models we consider, the above steps can be carried out sufficiently fast for the definition of an FPTAS.
Provided that the above algorithm yields an FPTAS for
![]() $\Xi$
, there is a generic polynomial-time approximate sampling algorithm for
$\Xi$
, there is a generic polynomial-time approximate sampling algorithm for
![]() $\nu$
that follows from a self-reducibility property of the polymer model; see ([Reference Helmuth, Perkins and Regts23], Theorem 10). We omit the details and summarise these facts as the following theorem which applies when
$\nu$
that follows from a self-reducibility property of the polymer model; see ([Reference Helmuth, Perkins and Regts23], Theorem 10). We omit the details and summarise these facts as the following theorem which applies when
![]() $\mathcal{P}$
is (a subset of) the connected subgraphs of some bounded-degree graph
$\mathcal{P}$
is (a subset of) the connected subgraphs of some bounded-degree graph
![]() $G$
. For a subgraph
$G$
. For a subgraph
![]() $\gamma$
, we use
$\gamma$
, we use
![]() $v_\gamma$
to denote the number of vertices in
$v_\gamma$
to denote the number of vertices in
![]() $\gamma$
. The important fact is that both the high-temperature and low-temperature polymer models we study satisfy the hypotheses of the result below.
$\gamma$
. The important fact is that both the high-temperature and low-temperature polymer models we study satisfy the hypotheses of the result below.
Theorem 7 ([Reference Jenssen, Keevash and Perkins24], Theorem 8 and [Reference Helmuth, Perkins and Regts23], Theorem 10). Fix
![]() $d$
and let
$d$
and let
![]() $\mathcal{G}$
be some class of graphs of maximum degree at most
$\mathcal{G}$
be some class of graphs of maximum degree at most
![]() $d$
. Suppose the following hold for a polymer model with partition function
$d$
. Suppose the following hold for a polymer model with partition function
![]() $\Xi (G)$
where the polymers
$\Xi (G)$
where the polymers
![]() $\mathcal{P}$
are connected subgraphs of some
$\mathcal{P}$
are connected subgraphs of some
![]() $G\in \mathcal{G}$
, and with decay function
$G\in \mathcal{G}$
, and with decay function
![]() $g$
.
$g$
.
-
(1) There exist constants
 $c_1, c_2 \gt 0$
such that given a connected subgraph
$c_1, c_2 \gt 0$
such that given a connected subgraph
 $\gamma$
, determining whether
$\gamma$
, determining whether
 $\gamma$
is a polymer in
$\gamma$
is a polymer in
 $\mathcal{P}$
, and computing
$\mathcal{P}$
, and computing
 $w_\gamma$
and
$w_\gamma$
and
 $g(\gamma )$
can be done in time
$g(\gamma )$
can be done in time
 $O(v_{\gamma }^{c_1}e^{c_2v_{\gamma }})$
.
$O(v_{\gamma }^{c_1}e^{c_2v_{\gamma }})$
. -
(2) There exists
 $\rho = \rho (d) \gt 0$
so that for every
$\rho = \rho (d) \gt 0$
so that for every
 $G\in \mathcal{G}$
and every
$G\in \mathcal{G}$
and every
 $\gamma \in \mathcal{P}$
,
$\gamma \in \mathcal{P}$
,
 $g(\gamma )\geq \rho v_{\gamma }$
.
$g(\gamma )\geq \rho v_{\gamma }$
. -
(3) The Kotecký–Preiss condition (5) holds with the given function
 $g$
.
$g$
.
Then there is an FPTAS for the partition function
![]() $\Xi (G)$
of the polymer model for
$\Xi (G)$
of the polymer model for
![]() $G\in \mathcal{G}$
that with approximation error
$G\in \mathcal{G}$
that with approximation error
![]() $\delta$
and
$\delta$
and
![]() $n=|V(G)|$
has running time
$n=|V(G)|$
has running time
![]() $n\cdot (n/\delta )^{O((\ln d+c_2)/\rho )}$
. There is also a polynomial-time sampling scheme for the associated polymer measure
$n\cdot (n/\delta )^{O((\ln d+c_2)/\rho )}$
. There is also a polynomial-time sampling scheme for the associated polymer measure
![]() $\nu$
.
$\nu$
.
3. Low-temperature algorithms
3.1 Sketch of low-temperature argument
For the low-temperature regime, we decompose the partition function into colourings that have a majority colour, and the remaining colourings. Our polymer model can only represent colourings with a majority colour, so it is vital to prove that the remaining colourings have a small contribution to the partition function, which is the content of our Lemma 8. Working with fewer colours and smaller expansion makes this step more challenging than in [Reference Jenssen, Keevash and Perkins24]. The core of the proof involves obtaining upper bounds on the number of vertex-colorings of a graph that induce few monochromatic edges. In light of the heuristic (b), which relates colourings with few monochromatic edges to cuts, this is done by analysing a Karger-like random sequence of edge contractions and the probability that this yields a particular cut.
We then handle each majority colour with a polymer model where the polymers are connected, induced subgraphs of
![]() $G$
whose vertices do not receive the majority colour. The weight of a polymer is related to the
$G$
whose vertices do not receive the majority colour. The weight of a polymer is related to the
![]() $(q-1)$
-spin partition function on that subgraph. Since we are working with colourings with a majority colour, the ‘defects’ (vertices that don’t have the majority colour) occupy at most half the vertices, which is a global constraint on the polymers that we wish to avoid. We pass to a different polymer model which requires only that each polymer has at most half the vertices. This partition function is clearly an overestimate; however, in Lemma 9 we show that this overestimation is negligible.
$(q-1)$
-spin partition function on that subgraph. Since we are working with colourings with a majority colour, the ‘defects’ (vertices that don’t have the majority colour) occupy at most half the vertices, which is a global constraint on the polymers that we wish to avoid. We pass to a different polymer model which requires only that each polymer has at most half the vertices. This partition function is clearly an overestimate; however, in Lemma 9 we show that this overestimation is negligible.
All that remains is to verify the Kotecký–Preiss condition for this polymer model. There is, however, another challenge here: the aforementioned
![]() $(q-1)$
-spin partition function plays a significant role in this computation, and one needs to bound it in order to proceed. Fortunately, our understanding of extremal bounds on such functions has progressed recently, most notably due to Sah et al. [Reference Sah, Sawhney, Stoner and Zhao40]. We use their results to derive bounds on the partition functions of the subgraphs that make up our polymers. For triangle-free graphs the available bounds are stronger, which lets us work with weaker expansion in this case, and ultimately with the hypercube. The extremal results we derive from [Reference Sah, Sawhney, Stoner and Zhao40] are the content of Lemmas 11 and 12.
$(q-1)$
-spin partition function plays a significant role in this computation, and one needs to bound it in order to proceed. Fortunately, our understanding of extremal bounds on such functions has progressed recently, most notably due to Sah et al. [Reference Sah, Sawhney, Stoner and Zhao40]. We use their results to derive bounds on the partition functions of the subgraphs that make up our polymers. For triangle-free graphs the available bounds are stronger, which lets us work with weaker expansion in this case, and ultimately with the hypercube. The extremal results we derive from [Reference Sah, Sawhney, Stoner and Zhao40] are the content of Lemmas 11 and 12.
The final ingredient in verifying the Kotecký–Preiss condition is a bound on the number of connected subsets of vertices in
![]() $G$
with a given edge-boundary size. At first glance, this looks similar to a lemma used in [Reference Jenssen and Perkins25, Reference Jenssen, Perkins and Potukuchi26] that gives a bound on the number of connected subsets of vertices with a given vertex-boundary size (in bipartite graphs), which followed from mild adaptations of existing container methods [Reference Sapozhenko35, Reference Sapozhenko36].
$G$
with a given edge-boundary size. At first glance, this looks similar to a lemma used in [Reference Jenssen and Perkins25, Reference Jenssen, Perkins and Potukuchi26] that gives a bound on the number of connected subsets of vertices with a given vertex-boundary size (in bipartite graphs), which followed from mild adaptations of existing container methods [Reference Sapozhenko35, Reference Sapozhenko36].
While the case of edge boundaries does not seem to follow directly from these methods, we have developed Theorem 3 inspired by these previous works. At a high-level, container methods work by finding an ‘encoding’ or ‘certificate’ for each object of the type we wish to enumerate. If these certificates are small then the number of certificates, and thus objects, must be relatively small. In our case, we group sets of vertices
![]() $A$
with a fixed edge-boundary
$A$
with a fixed edge-boundary
![]() $B$
of size
$B$
of size
![]() $b$
by identifying a ‘core’ subset
$b$
by identifying a ‘core’ subset
![]() $A_0\subset A$
of size
$A_0\subset A$
of size
![]() $O(b/d)$
. We show these core sets must be connected in
$O(b/d)$
. We show these core sets must be connected in
![]() $G^7$
, and hence their number can be controlled. In this sense, each core set
$G^7$
, and hence their number can be controlled. In this sense, each core set
![]() $A_0$
certifies a container which contains sets
$A_0$
certifies a container which contains sets
![]() $A$
(of the type whose number we wish to bound) obtained by growing
$A$
(of the type whose number we wish to bound) obtained by growing
![]() $A_0$
appropriately, see (19). To complete the bound on the number of sets
$A_0$
appropriately, see (19). To complete the bound on the number of sets
![]() $A$
of interest, we must bound for each core
$A$
of interest, we must bound for each core
![]() $A_0$
the number of possible
$A_0$
the number of possible
![]() $A$
, or equivalently edge boundaries
$A$
, or equivalently edge boundaries
![]() $B$
, that can be associated with
$B$
, that can be associated with
![]() $A_0$
. We achieve this using Karger’s algorithm involving randomised edge contractions to count cuts.
$A_0$
. We achieve this using Karger’s algorithm involving randomised edge contractions to count cuts.
3.2 Polymer model
In Theorem 1, we deal with the class of
![]() $d$
-regular
$d$
-regular
![]() $2$
-expanders and triangle-free
$2$
-expanders and triangle-free
![]() $d$
-regular
$d$
-regular
![]() $1$
-expanders. Both these families of graphs satisfy
$1$
-expanders. Both these families of graphs satisfy
In particular, this also holds for the hypercube
![]() $Q_d$
. Property (7) is immediate in
$Q_d$
. Property (7) is immediate in
![]() $d$
-regular 2-expanders and follows from Mantel’s theorem [Reference Mantel33] in the triangle-free 1-expanding case. To see this, note that the expansion condition suffices for
$d$
-regular 2-expanders and follows from Mantel’s theorem [Reference Mantel33] in the triangle-free 1-expanding case. To see this, note that the expansion condition suffices for
![]() $|A|\ge 2d-2$
, and if
$|A|\ge 2d-2$
, and if
![]() $|A|\lt 2d-2$
then we use the bound
$|A|\lt 2d-2$
then we use the bound
which follows from Mantel’s theorem. For
![]() $2\le |A| \le 2d-2$
, this lower bound is at least
$2\le |A| \le 2d-2$
, this lower bound is at least
![]() $2d-2$
and property (7) follows.
$2d-2$
and property (7) follows.
The min-cut of a graph is the minimum number of edges that need to be deleted in order to disconnect the remaining graph. Any
![]() $d$
-regular graph
$d$
-regular graph
![]() $G$
that satisfies (7) also satisfies
$G$
that satisfies (7) also satisfies
In other words, the smallest set of edges that can be deleted to disconnect the graph is simply the set of all edges incident to any given vertex. Throughout this section we will use that
![]() $G$
satisfies (7), and therefore (8).
$G$
satisfies (7), and therefore (8).
We now define a polymer model for the low-temperature regime, following [Reference Jenssen, Keevash and Perkins24]. Here we take
![]() $\epsilon \in (0,1)$
; then, for some
$\epsilon \in (0,1)$
; then, for some
![]() $d_0(\epsilon )$
and an absolute constant
$d_0(\epsilon )$
and an absolute constant
![]() $c$
, we have
$c$
, we have
![]() $d\ge d_0$
,
$d\ge d_0$
,
![]() $q\ge d^c$
, and
$q\ge d^c$
, and
![]() $\beta \ge (1\,{+}\,\epsilon )\beta _o(q,d)$
. We also assume that
$\beta \ge (1\,{+}\,\epsilon )\beta _o(q,d)$
. We also assume that
![]() $q$
is large enough (by ensuring that
$q$
is large enough (by ensuring that
![]() $d_0$
and
$d_0$
and
![]() $c$
are large enough) that this implies
$c$
are large enough) that this implies
![]() $\beta \ge (2+\epsilon )\ln (q)/d$
.
$\beta \ge (2+\epsilon )\ln (q)/d$
.
Let a polymer
![]() $\gamma$
be a connected, induced subgraph of
$\gamma$
be a connected, induced subgraph of
![]() $G$
with at most
$G$
with at most
![]() $n/2$
vertices. For each polymer
$n/2$
vertices. For each polymer
![]() $\gamma$
, let
$\gamma$
, let
![]() $v_\gamma$
and
$v_\gamma$
and
![]() $e_\gamma$
be the number of vertices and edges respectively. Let
$e_\gamma$
be the number of vertices and edges respectively. Let
![]() $\nabla _{\gamma }$
denote the number of boundary edges (i.e. edges of
$\nabla _{\gamma }$
denote the number of boundary edges (i.e. edges of
![]() $G$
with one endpoint in the vertex set of
$G$
with one endpoint in the vertex set of
![]() $\gamma$
), and let
$\gamma$
), and let
![]() $\eta _{\gamma } \,{:\!=}\, \nabla _{\gamma }/v_\gamma$
, be a measure of the expansion of the vertex set of
$\eta _{\gamma } \,{:\!=}\, \nabla _{\gamma }/v_\gamma$
, be a measure of the expansion of the vertex set of
![]() $\gamma$
in
$\gamma$
in
![]() $G$
. The polymer weights
$G$
. The polymer weights
![]() $w_\gamma$
are given by
$w_\gamma$
are given by
where we interpret
![]() $\gamma$
as a graph and hence
$\gamma$
as a graph and hence
![]() $Z_{\gamma }(q-1, \beta )$
is the Potts partition function of
$Z_{\gamma }(q-1, \beta )$
is the Potts partition function of
![]() $\gamma$
with
$\gamma$
with
![]() $q-1$
colours. We say that two polymers
$q-1$
colours. We say that two polymers
![]() $\gamma$
and
$\gamma$
and
![]() $\gamma^{\prime}$
are incompatible if
$\gamma^{\prime}$
are incompatible if
![]() $\mathrm{dist}_G(\gamma, \gamma^{\prime}) \leq 1$
. That is,
$\mathrm{dist}_G(\gamma, \gamma^{\prime}) \leq 1$
. That is,
![]() $\gamma \not \sim \gamma^{\prime}$
if and only if they share a vertex or one contains a neighbour of the other. As before, we write
$\gamma \not \sim \gamma^{\prime}$
if and only if they share a vertex or one contains a neighbour of the other. As before, we write
![]() $\Omega$
for the collection of pairwise compatible sets of polymers and
$\Omega$
for the collection of pairwise compatible sets of polymers and
![]() $\Xi = \Xi _{G}(q,\beta )$
for the partition function of this polymer model.
$\Xi = \Xi _{G}(q,\beta )$
for the partition function of this polymer model.
For our low-temperature algorithm, there is not a precise correspondence between
![]() $Z_G(q,\beta )$
and
$Z_G(q,\beta )$
and
![]() $\Xi$
, and we must establish that approximating
$\Xi$
, and we must establish that approximating
![]() $\Xi$
does in fact yield an approximation of
$\Xi$
does in fact yield an approximation of
![]() $Z_G(q,\beta )$
. The set
$Z_G(q,\beta )$
. The set
![]() $[q]^{V(G)}$
of
$[q]^{V(G)}$
of
![]() $q$
-colorings of
$q$
-colorings of
![]() $V(G)$
admits a partition into
$V(G)$
admits a partition into
![]() $S_0, S_1, \dotsc, S_q$
where
$S_0, S_1, \dotsc, S_q$
where
![]() $S_0$
is the set of colourings such that each colour occupies at most
$S_0$
is the set of colourings such that each colour occupies at most
![]() $n/2$
vertices and for
$n/2$
vertices and for
![]() $j\in [q]$
,
$j\in [q]$
,
![]() $S_j$
is the set of colourings in which
$S_j$
is the set of colourings in which
![]() $j$
is the majority colour (i.e.
$j$
is the majority colour (i.e.
![]() $S_j = \{\sigma \in [q]^{V(G)}\,{:}\, |\sigma ^{-1}(j)| \gt n/2\}$
). We have the following lemma whose proof is postponed to Section 4.2.
$S_j = \{\sigma \in [q]^{V(G)}\,{:}\, |\sigma ^{-1}(j)| \gt n/2\}$
). We have the following lemma whose proof is postponed to Section 4.2.
Lemma 8.
There exists an absolute constant
![]() $c$
such that the following holds. For every
$c$
such that the following holds. For every
![]() $\epsilon \in (0,1)$
there exists
$\epsilon \in (0,1)$
there exists
![]() $d_0(\epsilon )$
such that for every
$d_0(\epsilon )$
such that for every
![]() $d\ge d_0$
,
$d\ge d_0$
,
![]() $q\ge d^c$
and
$q\ge d^c$
and
![]() $\beta \ge (1+\epsilon )\beta _o(q,d)$
, we have
$\beta \ge (1+\epsilon )\beta _o(q,d)$
, we have
Let us define the partition function-like quantity
 \begin{equation*} \widetilde {\Xi } = \widetilde {\Xi }_G(q,\beta ) \,{:\!=}\, \sum _{\substack {\Lambda \in \Omega \\ \|\Lambda \| \lt n/2}}\prod _{\gamma \in \Lambda }w_{\gamma }, \end{equation*}
\begin{equation*} \widetilde {\Xi } = \widetilde {\Xi }_G(q,\beta ) \,{:\!=}\, \sum _{\substack {\Lambda \in \Omega \\ \|\Lambda \| \lt n/2}}\prod _{\gamma \in \Lambda }w_{\gamma }, \end{equation*}
where
![]() $\|\Lambda \| = \sum _{\gamma \in \Lambda }v_{\gamma }$
is the size of a set
$\|\Lambda \| = \sum _{\gamma \in \Lambda }v_{\gamma }$
is the size of a set
![]() $\Lambda$
of pairwise compatible polymers. We write
$\Lambda$
of pairwise compatible polymers. We write
![]() $\widetilde \Omega = \{\Lambda \in \Omega\,{:}\, \|\Lambda \| \lt n/2\}$
and note that
$\widetilde \Omega = \{\Lambda \in \Omega\,{:}\, \|\Lambda \| \lt n/2\}$
and note that
![]() $\widetilde \Xi$
is not the true partition function of the polymer model because of the global constraint
$\widetilde \Xi$
is not the true partition function of the polymer model because of the global constraint
![]() $\|\Lambda \| \lt n/2$
. In terms of the Potts partition function
$\|\Lambda \| \lt n/2$
. In terms of the Potts partition function
![]() $Z_G(q,\beta )$
, the quantity
$Z_G(q,\beta )$
, the quantity
![]() $\widetilde{\Xi }$
faithfully represents the colourings of
$\widetilde{\Xi }$
faithfully represents the colourings of
![]() $G$
which have a majority colour because
$G$
which have a majority colour because
 \begin{equation*} \sum _{j\in [q]}\sum _{\sigma \in S_j}e^{\beta m(G,\sigma )} = e^{\beta dn/2} \sum _{j\in [q]}\sum _{\substack {\Lambda \in \Omega \\ \|\Lambda \| \lt n/2}} \prod _{\gamma \in \Lambda }w_\gamma = q e^{\beta dn/2}\widetilde {\Xi }. \end{equation*}
\begin{equation*} \sum _{j\in [q]}\sum _{\sigma \in S_j}e^{\beta m(G,\sigma )} = e^{\beta dn/2} \sum _{j\in [q]}\sum _{\substack {\Lambda \in \Omega \\ \|\Lambda \| \lt n/2}} \prod _{\gamma \in \Lambda }w_\gamma = q e^{\beta dn/2}\widetilde {\Xi }. \end{equation*}
To see this, consider a colouring
![]() $\sigma \in [q]^{V}$
with majority colour
$\sigma \in [q]^{V}$
with majority colour
![]() $j$
and decompose
$j$
and decompose
![]() $\sigma ^{-1}([q]\setminus \{j\})\,{\subset}\,V$
into sets such that their pairwise distance in
$\sigma ^{-1}([q]\setminus \{j\})\,{\subset}\,V$
into sets such that their pairwise distance in
![]() $G$
is at least two. These sets induce subgraphs which form pairwise compatible polymers. Hence for any
$G$
is at least two. These sets induce subgraphs which form pairwise compatible polymers. Hence for any
![]() $j\in [q]$
the colourings with majority colour
$j\in [q]$
the colourings with majority colour
![]() $j$
are in bijection with
$j$
are in bijection with
![]() $\{\Lambda \in \Omega\,{:}\, \|\Lambda \| \lt n/2\}$
. The weight function and incompatibility criterion have been carefully defined to make the above calculation work on the level of partition function contribution as well.
$\{\Lambda \in \Omega\,{:}\, \|\Lambda \| \lt n/2\}$
. The weight function and incompatibility criterion have been carefully defined to make the above calculation work on the level of partition function contribution as well.
Rewriting Lemma 8 in this terminology gives us that
Thus, approximating
![]() $\widetilde \Xi$
is a viable avenue for approximating
$\widetilde \Xi$
is a viable avenue for approximating
![]() $Z_G(q,\beta )$
. There is one final complication, however, related to the fact that
$Z_G(q,\beta )$
. There is one final complication, however, related to the fact that
![]() $\widetilde \Xi$
is not precisely the partition function
$\widetilde \Xi$
is not precisely the partition function
![]() $\Xi$
of the low-temperature polymer model defined above. Since the standard algorithmic setup (Theorem 7) allows us to approximate
$\Xi$
of the low-temperature polymer model defined above. Since the standard algorithmic setup (Theorem 7) allows us to approximate
![]() $\Xi$
and approximately sample from the associated polymer measure
$\Xi$
and approximately sample from the associated polymer measure
![]() $\nu$
, we must additionally show that restricting to
$\nu$
, we must additionally show that restricting to
![]() $\Lambda$
such that
$\Lambda$
such that
![]() $\|\Lambda \|\lt n/2$
does not harm the approximation too much. The proof of the low-temperature case of Theorem 1 therefore follows from the following two lemmas and the standard algorithmic setup of Theorem 7.
$\|\Lambda \|\lt n/2$
does not harm the approximation too much. The proof of the low-temperature case of Theorem 1 therefore follows from the following two lemmas and the standard algorithmic setup of Theorem 7.
Lemma 9.
For
![]() $\Xi$
and
$\Xi$
and
![]() $\widetilde{\Xi }$
as defined above, we have
$\widetilde{\Xi }$
as defined above, we have
Lemma 10.
For every
![]() $\epsilon \in (0,1)$
, there exist
$\epsilon \in (0,1)$
, there exist
![]() $d_0(\epsilon )$
and an absolute constant
$d_0(\epsilon )$
and an absolute constant
![]() $c$
such that for every
$c$
such that for every
![]() $d\ge d_0$
,
$d\ge d_0$
,
![]() $q\ge d^c$
and
$q\ge d^c$
and
![]() $\beta \ge (1+\epsilon )\beta _o(q,d)$
, the Kotecký–Preiss condition (see (5) in Theorem 6
) holds for the low-temperature polymer model with
$\beta \ge (1+\epsilon )\beta _o(q,d)$
, the Kotecký–Preiss condition (see (5) in Theorem 6
) holds for the low-temperature polymer model with
![]() $f(\gamma )=\frac{\epsilon v_\gamma \ln q}{4d}$
and
$f(\gamma )=\frac{\epsilon v_\gamma \ln q}{4d}$
and
![]() $g(\gamma )=\frac{\epsilon \nabla _\gamma \ln q}{4d} + \frac{v_\gamma }{d}$
.
$g(\gamma )=\frac{\epsilon \nabla _\gamma \ln q}{4d} + \frac{v_\gamma }{d}$
.
Note that the left-hand side of condition (5) decreases if
![]() $g$
decreases, and hence the above lemma also implies that Theorem 6 holds for any smaller choice of
$g$
decreases, and hence the above lemma also implies that Theorem 6 holds for any smaller choice of
![]() $g$
. We prove the above results, starting with Lemma 10, in the following subsections.
$g$
. We prove the above results, starting with Lemma 10, in the following subsections.
3.3 Proof of Lemma 10
We first give the proof in the case that
![]() $G$
is a 2-expander, and then show the modifications necessary for triangle-free 1-expanders.
$G$
is a 2-expander, and then show the modifications necessary for triangle-free 1-expanders.
We use
![]() $N(\gamma ) = N_G(\gamma ) = \{v\,{:}\,\exists u \in \gamma \text{ such that }\{u,v\} \in E\}$
for the neighbourhood of
$N(\gamma ) = N_G(\gamma ) = \{v\,{:}\,\exists u \in \gamma \text{ such that }\{u,v\} \in E\}$
for the neighbourhood of
![]() $\gamma$
in
$\gamma$
in
![]() $G$
and
$G$
and
![]() $N_G[\gamma ] = N_G(\gamma ) \cup V(\gamma )$
for the closed neighbourhood of
$N_G[\gamma ] = N_G(\gamma ) \cup V(\gamma )$
for the closed neighbourhood of
![]() $\gamma$
. We upper bound the left-hand side of condition (5), here noting that the incompatibility relation on polymers yields
$\gamma$
. We upper bound the left-hand side of condition (5), here noting that the incompatibility relation on polymers yields
 \begin{equation*} \sum _{\gamma^{\prime}\not \sim \gamma }w_{\gamma^{\prime}} e^{f(\gamma^{\prime})+g(\gamma^{\prime})} \le \sum _{u\in N_G[\gamma ]}\sum _{\gamma^{\prime} \ni u} w_{\gamma^{\prime}} e^{f(\gamma^{\prime}) + g(\gamma^{\prime})} = \sum _{u\in N_G[\gamma ]}\sum _{b\ge d}\sum _{\substack {\gamma^{\prime} \ni u \\ \text {s.t.} \nabla _{\gamma^{\prime}}=b}} w_{\gamma^{\prime}} e^{f(\gamma^{\prime}) + g(\gamma^{\prime})}, \end{equation*}
\begin{equation*} \sum _{\gamma^{\prime}\not \sim \gamma }w_{\gamma^{\prime}} e^{f(\gamma^{\prime})+g(\gamma^{\prime})} \le \sum _{u\in N_G[\gamma ]}\sum _{\gamma^{\prime} \ni u} w_{\gamma^{\prime}} e^{f(\gamma^{\prime}) + g(\gamma^{\prime})} = \sum _{u\in N_G[\gamma ]}\sum _{b\ge d}\sum _{\substack {\gamma^{\prime} \ni u \\ \text {s.t.} \nabla _{\gamma^{\prime}}=b}} w_{\gamma^{\prime}} e^{f(\gamma^{\prime}) + g(\gamma^{\prime})}, \end{equation*}
Since
![]() $|N_G[\gamma ]| \le v_\gamma + \nabla _\gamma$
, it suffices to show that for all
$|N_G[\gamma ]| \le v_\gamma + \nabla _\gamma$
, it suffices to show that for all
![]() $u\in V$
we have
$u\in V$
we have
 \begin{equation} \sum _{b\ge d}\sum _{\substack{\gamma^{\prime} \ni u \\ \text{s.t.} \nabla _{\gamma^{\prime}}=b}} w_{\gamma^{\prime}} e^{f(\gamma^{\prime}) + g(\gamma^{\prime})} \leq \min _{\gamma \in \mathcal{P}} \frac{f(\gamma )}{v_{\gamma } + \nabla _{\gamma }}. \end{equation}
\begin{equation} \sum _{b\ge d}\sum _{\substack{\gamma^{\prime} \ni u \\ \text{s.t.} \nabla _{\gamma^{\prime}}=b}} w_{\gamma^{\prime}} e^{f(\gamma^{\prime}) + g(\gamma^{\prime})} \leq \min _{\gamma \in \mathcal{P}} \frac{f(\gamma )}{v_{\gamma } + \nabla _{\gamma }}. \end{equation}
We use the following lemma, whose proof is postponed to Section 5, to bound the weights
![]() $w_{\gamma^{\prime}}$
that appear in (9).
$w_{\gamma^{\prime}}$
that appear in (9).
Lemma 11.
For any polymer
![]() $\gamma \in \mathcal{P}$
we have
$\gamma \in \mathcal{P}$
we have
To bound the exponent of
![]() $q$
in Lemma 11, observe that
$q$
in Lemma 11, observe that
![]() $d v_\gamma = 2e_\gamma + \nabla _\gamma \ge 2e_\gamma$
by a double-counting argument, and recall that
$d v_\gamma = 2e_\gamma + \nabla _\gamma \ge 2e_\gamma$
by a double-counting argument, and recall that
![]() $\eta _{\gamma } = \nabla _{\gamma }/v_\gamma$
to obtain
$\eta _{\gamma } = \nabla _{\gamma }/v_\gamma$
to obtain
Plugging these facts and Lemma 11 into the definition of
![]() $w_\gamma$
gives
$w_\gamma$
gives
and using
![]() $\beta \ge (2+\epsilon )\ln (q)/ d$
we have
$\beta \ge (2+\epsilon )\ln (q)/ d$
we have
We assume
![]() $q$
is large enough (by assuming
$q$
is large enough (by assuming
![]() $d_0$
and
$d_0$
and
![]() $c$
are large enough) so that
$c$
are large enough) so that
![]() $2^{\frac{\nabla _\gamma }{d\eta _\gamma }}\leq q^{\frac{\nabla _\gamma }{d} \cdot \frac{\epsilon }{4}}$
, and thus
$2^{\frac{\nabla _\gamma }{d\eta _\gamma }}\leq q^{\frac{\nabla _\gamma }{d} \cdot \frac{\epsilon }{4}}$
, and thus
Using our choice of
![]() $f$
and
$f$
and
![]() $g$
, we also have
$g$
, we also have
which combined with the bound
![]() $\eta _\gamma \ge 2$
gives
$\eta _\gamma \ge 2$
gives
where the final inequality holds again when
![]() $q$
is large enough in terms of
$q$
is large enough in terms of
![]() $\epsilon$
.
$\epsilon$
.
We now use our container-type result. Applying Theorem 3 and (10) to bound the left-hand side of (9), we have (for
![]() $q$
large enough that the series converges)
$q$
large enough that the series converges)
 \begin{equation*} \sum _{b\ge d}\sum _{\substack {\gamma^{\prime} \ni u \\ \text {s.t.} \nabla _{\gamma^{\prime}}=b}} w_{\gamma^{\prime}} e^{f(\gamma^{\prime}) + g(\gamma^{\prime})} \leq \sum _{b\ge d} d^{O\left ((1+1/\eta )b/d\right )} q^{-\frac {b}{2d}} \le \frac {d^{c'}/\sqrt q}{1-(d^{c'}/\sqrt q)^{1/d}},\end{equation*}
\begin{equation*} \sum _{b\ge d}\sum _{\substack {\gamma^{\prime} \ni u \\ \text {s.t.} \nabla _{\gamma^{\prime}}=b}} w_{\gamma^{\prime}} e^{f(\gamma^{\prime}) + g(\gamma^{\prime})} \leq \sum _{b\ge d} d^{O\left ((1+1/\eta )b/d\right )} q^{-\frac {b}{2d}} \le \frac {d^{c'}/\sqrt q}{1-(d^{c'}/\sqrt q)^{1/d}},\end{equation*}
where the absolute constant
![]() $c'\ge 4$
is large enough that the term
$c'\ge 4$
is large enough that the term
![]() $O\left ((1+1/\eta )b/d\right )$
is at most
$O\left ((1+1/\eta )b/d\right )$
is at most
![]() $c'b/d$
for all
$c'b/d$
for all
![]() $b\ge d$
and all
$b\ge d$
and all
![]() $\eta \ge 1$
. Note that the right-hand side above is a decreasing function of
$\eta \ge 1$
. Note that the right-hand side above is a decreasing function of
![]() $q$
. To satisfy (9) we want this to be at most
$q$
. To satisfy (9) we want this to be at most
which is an increasing function of
![]() $q$
. Thus, it suffices to take
$q$
. Thus, it suffices to take
![]() $q$
larger than some known value for the desired inequality holds. It is straightforward to check that
$q$
larger than some known value for the desired inequality holds. It is straightforward to check that
![]() $q=d^{3c'}$
suffices for all
$q=d^{3c'}$
suffices for all
![]() $d$
large enough.
$d$
large enough.
3.4 The triangle-free case
If
![]() $G$
is triangle free then a stronger upper bound on partition functions of the form
$G$
is triangle free then a stronger upper bound on partition functions of the form
![]() $Z_{\gamma }(q-1, \beta )$
holds.
$Z_{\gamma }(q-1, \beta )$
holds.
Lemma 12.
If
![]() $G$
is triangle free, then
$G$
is triangle free, then
Plugging this inequality in the computation in the previous section, we have
and hence only assuming
![]() $\eta \ge 1$
we have the bound
$\eta \ge 1$
we have the bound
We may then apply Theorem 3 to reach the same conclusion as before.
3.5 Proof of Lemma 9
Let
![]() $\nu$
and
$\nu$
and
![]() $\widetilde{\nu }$
denote the probability distributions on
$\widetilde{\nu }$
denote the probability distributions on
![]() $\Omega$
given by the partition functions
$\Omega$
given by the partition functions
![]() $\Xi$
and
$\Xi$
and
![]() $\widetilde{\Xi }$
respectively, meaning that
$\widetilde{\Xi }$
respectively, meaning that
![]() $\nu (\Lambda ) = \prod _{\gamma \in \Lambda }w_\gamma/ \Xi$
for any
$\nu (\Lambda ) = \prod _{\gamma \in \Lambda }w_\gamma/ \Xi$
for any
![]() $\Lambda \in \Omega$
and
$\Lambda \in \Omega$
and
![]() $\widetilde{\nu }(\Lambda )=0$
if
$\widetilde{\nu }(\Lambda )=0$
if
![]() $\|\Lambda \|\ge n/2$
but
$\|\Lambda \|\ge n/2$
but
![]() $\widetilde{\nu }(\Lambda ) = \prod _{\gamma \in \Lambda }w_\gamma/ \widetilde{\Xi }$
otherwise. We briefly prove a large deviation inequality on the size of the defects, similar to [Reference Jenssen and Perkins25, Reference Jenssen, Perkins and Potukuchi26]. Here, we carefully make use of the term
$\widetilde{\nu }(\Lambda ) = \prod _{\gamma \in \Lambda }w_\gamma/ \widetilde{\Xi }$
otherwise. We briefly prove a large deviation inequality on the size of the defects, similar to [Reference Jenssen and Perkins25, Reference Jenssen, Perkins and Potukuchi26]. Here, we carefully make use of the term
![]() $e^{v_\gamma/d}$
in the definition of
$e^{v_\gamma/d}$
in the definition of
![]() $g(\gamma )$
and the monotonicity of condition (5) in
$g(\gamma )$
and the monotonicity of condition (5) in
![]() $g$
. This immediately implies that Theorem 6 holds for an alternative polymer model on the same polymers but with weights
$g$
. This immediately implies that Theorem 6 holds for an alternative polymer model on the same polymers but with weights
because for the same choice
![]() $f(\gamma )=\frac{\epsilon v_\gamma \ln q}{4d}$
and now taking
$f(\gamma )=\frac{\epsilon v_\gamma \ln q}{4d}$
and now taking
![]() $g(\gamma ) = \frac{\epsilon \nabla _\gamma \ln q}{4d}$
, condition (5) is the same for both models.
$g(\gamma ) = \frac{\epsilon \nabla _\gamma \ln q}{4d}$
, condition (5) is the same for both models.
Write
and let
![]() $\boldsymbol{\Lambda }$
denote a random set of pairwise compatible polymers drawn from
$\boldsymbol{\Lambda }$
denote a random set of pairwise compatible polymers drawn from
![]() $\nu$
. Observe that
$\nu$
. Observe that
![]() $\Xi^{\prime}$
naturally appears in an expression for
$\Xi^{\prime}$
naturally appears in an expression for
![]() $\mathbb{E} e^{\|\boldsymbol{\Lambda }\|/d}$
as follows:
$\mathbb{E} e^{\|\boldsymbol{\Lambda }\|/d}$
as follows:
Then Theorem 6 and the fact that
![]() $\Xi \ge 1$
gives us
$\Xi \ge 1$
gives us
where the final equality is the cluster expansion for the abstract polymer model defined by
![]() $\Xi^{\prime}$
, and hence the sum is over clusters
$\Xi^{\prime}$
, and hence the sum is over clusters
![]() $\Gamma \in \mathcal{C}$
as defined in Section 2. We can crudely upper bound this cluster expansion of by summing over all polymers of the form
$\Gamma \in \mathcal{C}$
as defined in Section 2. We can crudely upper bound this cluster expansion of by summing over all polymers of the form
![]() $\gamma =(\{v\},\emptyset )$
induced by a vertex and applying the tail bound (6). This gives
$\gamma =(\{v\},\emptyset )$
induced by a vertex and applying the tail bound (6). This gives
 \begin{align} \ln \Xi^{\prime} &\leq \sum _{v\in V(G)}\sum _{\substack{\Gamma \in \mathcal{C}\\ \Gamma \not \sim (\{v\},\emptyset )}} \left |\phi (\Gamma )\prod _{\gamma \in \Gamma }w^{\prime}_{\gamma }\right | \end{align}
\begin{align} \ln \Xi^{\prime} &\leq \sum _{v\in V(G)}\sum _{\substack{\Gamma \in \mathcal{C}\\ \Gamma \not \sim (\{v\},\emptyset )}} \left |\phi (\Gamma )\prod _{\gamma \in \Gamma }w^{\prime}_{\gamma }\right | \end{align}
 \begin{align} &\leq \sum _{v\in V(G)}\sum _{\substack{\Gamma \in \mathcal{C}\\ \Gamma \not \sim (\{v\},\emptyset )}} q^{-\epsilon/4}\left |\phi (\Gamma )\prod _{\gamma \in \Gamma }w^{\prime}_{\gamma }\right |e^{g(\Gamma )} \end{align}
\begin{align} &\leq \sum _{v\in V(G)}\sum _{\substack{\Gamma \in \mathcal{C}\\ \Gamma \not \sim (\{v\},\emptyset )}} q^{-\epsilon/4}\left |\phi (\Gamma )\prod _{\gamma \in \Gamma }w^{\prime}_{\gamma }\right |e^{g(\Gamma )} \end{align}
Line (12) holds because every cluster
![]() $\Gamma \not \sim (\{v\},\emptyset )$
contains at least one polymer (which has at least one vertex) and hence using (8) we have
$\Gamma \not \sim (\{v\},\emptyset )$
contains at least one polymer (which has at least one vertex) and hence using (8) we have
To obtain line (13) we use (6) with
![]() $f((\{v\},\emptyset )) = \frac{\epsilon \ln q}{4d}$
.
$f((\{v\},\emptyset )) = \frac{\epsilon \ln q}{4d}$
.
Combining the above calculations, we have
![]() $\mathbb{E} e^{\|\boldsymbol{\Lambda }\|/d} \le e^{\frac{n}{4d}}$
, and hence Markov’s inequality gives
$\mathbb{E} e^{\|\boldsymbol{\Lambda }\|/d} \le e^{\frac{n}{4d}}$
, and hence Markov’s inequality gives
which implies
![]() $\nu (\widetilde \Omega )\ge 1-e^{-n/(4d)}$
. Here we have used the fact that
$\nu (\widetilde \Omega )\ge 1-e^{-n/(4d)}$
. Here we have used the fact that
![]() $q$
is large in terms of
$q$
is large in terms of
![]() $\epsilon$
so
$\epsilon$
so
![]() $\frac{\epsilon \ln q}{4q^{\epsilon/4}} \leq \frac{1}{4}$
. We would like to point out that similar computations are required for the proofs of Theorems 4 and 5.
$\frac{\epsilon \ln q}{4q^{\epsilon/4}} \leq \frac{1}{4}$
. We would like to point out that similar computations are required for the proofs of Theorems 4 and 5.
Since the probabilities for
![]() $\widetilde \nu$
on outcomes in
$\widetilde \nu$
on outcomes in
![]() $\widetilde \Omega$
are made by redistributing the probability mass
$\widetilde \Omega$
are made by redistributing the probability mass
![]() $\nu (\Omega \setminus \widetilde \Omega )\le e^{-n/(4d)}$
onto outcomes in
$\nu (\Omega \setminus \widetilde \Omega )\le e^{-n/(4d)}$
onto outcomes in
![]() $\widetilde \Omega$
, we immediately have a bound on the total variation distance
$\widetilde \Omega$
, we immediately have a bound on the total variation distance
The conclusion follows because by the definitions of
![]() $\widetilde \nu$
and total variation distance we have
$\widetilde \nu$
and total variation distance we have
and hence dividing by
![]() $\nu (\widetilde \Omega )$
gives
$\nu (\widetilde \Omega )$
gives
4. Enumerative results
In this section, we prove Theorem 3 and Lemma 8.
4.1 Connected sets with small edge boundaries: Proof of Theorem 3
The main combinatorial result underlying our container-like lemma is the following standard adaptation of Karger’s algorithm to count
![]() $\alpha$
-min-cuts.
$\alpha$
-min-cuts.
Theorem 13 (Karger [Reference Karger27]). Let
![]() $G$
be a graph whose min-cut has
$G$
be a graph whose min-cut has
![]() $t$
edges, and let
$t$
edges, and let
![]() $\alpha \geq 1$
be a real number. The number of cuts in
$\alpha \geq 1$
be a real number. The number of cuts in
![]() $G$
with at most
$G$
with at most
![]() $\alpha t$
edges is at most
$\alpha t$
edges is at most
![]() $\binom{n}{2\alpha } \cdot 2^{2\alpha }$
.
$\binom{n}{2\alpha } \cdot 2^{2\alpha }$
.
We also require a well-known result giving an upper bound to the number of connected induced subgraphs containing a fixed vertex.
Proposition 14 ([Reference Knuth28], Vol. 3 p. 396, Ex.11). The number of rooted labelled trees of maximum degree
![]() $\Delta$
on
$\Delta$
on
![]() $n \geq 1$
vertices is
$n \geq 1$
vertices is
and hence, for a graph of maximum degree
![]() $\Delta$
and a fixed vertex
$\Delta$
and a fixed vertex
![]() $v$
, the number of connected induced subgraphs on
$v$
, the number of connected induced subgraphs on
![]() $n$
vertices containing
$n$
vertices containing
![]() $v$
is also at most this number.
$v$
is also at most this number.
With this, we now prove Theorem 3.
Proof of Theorem
3. We first introduce some notation. Recall
![]() $V$
and
$V$
and
![]() $E$
are the sets of vertices and edges of
$E$
are the sets of vertices and edges of
![]() $G$
respectively. For
$G$
respectively. For
![]() $u, v \in V$
, we use
$u, v \in V$
, we use
![]() $\mathrm{dist}_G(u, v)$
to denote the distance in
$\mathrm{dist}_G(u, v)$
to denote the distance in
![]() $G$
from
$G$
from
![]() $u$
to
$u$
to
![]() $v$
, that is, the number of edges on a shortest path between
$v$
, that is, the number of edges on a shortest path between
![]() $u$
and
$u$
and
![]() $v$
. For every
$v$
. For every
![]() $k \in \mathbb{N}$
, we define the
$k \in \mathbb{N}$
, we define the
![]() $k$
th neighbourhood of
$k$
th neighbourhood of
![]() $u$
in
$u$
in
![]() $G$
as
$G$
as
![]() $N_{G}^k(u) = \{v \in V\,{:}\, 1 \leq \mathrm{dist}_G(u, v) \leq k\}$
. Then
$N_{G}^k(u) = \{v \in V\,{:}\, 1 \leq \mathrm{dist}_G(u, v) \leq k\}$
. Then
![]() $N_G(u) = N_G^1(u)$
. We may also define the
$N_G(u) = N_G^1(u)$
. We may also define the
![]() $k$
th neighbourhood of a set of vertices
$k$
th neighbourhood of a set of vertices
![]() $A \subseteq V$
as
$A \subseteq V$
as
![]() $N_G^k(A) = \cup _{u \in A}N_G^k(u)$
. The
$N_G^k(A) = \cup _{u \in A}N_G^k(u)$
. The
![]() $k$
th power of the graph
$k$
th power of the graph
![]() $G$
is the graph
$G$
is the graph
![]() $G^k$
on vertex set
$G^k$
on vertex set
![]() $V$
where
$V$
where
![]() $\{u,v\} \in E(G^k)$
if and only if
$\{u,v\} \in E(G^k)$
if and only if
![]() $1 \leq \mathrm{dist}_G(u, v) \leq k$
. Observe that
$1 \leq \mathrm{dist}_G(u, v) \leq k$
. Observe that
![]() $N_{G^k}(u) = N_G^k(u)$
.
$N_{G^k}(u) = N_G^k(u)$
.
Let
![]() $I$
be the vertex-edge incidence graph of
$I$
be the vertex-edge incidence graph of
![]() $G$
, which is a bipartite graph with vertex set
$G$
, which is a bipartite graph with vertex set
![]() $V \sqcup E$
and edges
$V \sqcup E$
and edges
![]() $\left \{(u,e) \in V\times E\mid u \in e\right \}$
. Let
$\left \{(u,e) \in V\times E\mid u \in e\right \}$
. Let
![]() $J$
be the bipartite graph with vertex set
$J$
be the bipartite graph with vertex set
![]() $V \sqcup E$
and edges given by
$V \sqcup E$
and edges given by
![]() $\left \{(u,e)\in V\times E\mid \exists v\in N_G(u) \text{ s.t. } v\in e\right \}$
. That is,
$\left \{(u,e)\in V\times E\mid \exists v\in N_G(u) \text{ s.t. } v\in e\right \}$
. That is,
![]() $(u,e)$
forms an edge of
$(u,e)$
forms an edge of
![]() $J$
if and only if
$J$
if and only if
![]() $e$
is an edge incident in
$e$
is an edge incident in
![]() $G$
to a neighbour of
$G$
to a neighbour of
![]() $u$
(this includes all edges incident to
$u$
(this includes all edges incident to
![]() $u$
itself). Note that
$u$
itself). Note that
![]() $I$
is a subgraph of
$I$
is a subgraph of
![]() $J$
.
$J$
.
Observe that for every
![]() $u\in V$
, the degree of
$u\in V$
, the degree of
![]() $u$
in
$u$
in
![]() $J$
is at least
$J$
is at least
![]() $\binom{d+1}{2} \ge d^2/2$
and at most
$\binom{d+1}{2} \ge d^2/2$
and at most
![]() $d^2$
. To see the lower bound, consider that each of the
$d^2$
. To see the lower bound, consider that each of the
![]() $d$
neighbours of
$d$
neighbours of
![]() $u$
is itself incident to
$u$
is itself incident to
![]() $d$
edges, and the number of distinct edges incident to
$d$
edges, and the number of distinct edges incident to
![]() $N_G(u)$
is minimised when
$N_G(u)$
is minimised when
![]() $N_G(u)$
forms a clique on
$N_G(u)$
forms a clique on
![]() $d+1$
vertices. The upper bound holds because the maximum number of edges of
$d+1$
vertices. The upper bound holds because the maximum number of edges of
![]() $G$
incident to
$G$
incident to
![]() $N_G(u)$
is
$N_G(u)$
is
![]() $d^2$
(which occurs if and only if
$d^2$
(which occurs if and only if
![]() $u$
is contained in no cycles of length 3 or 4).
$u$
is contained in no cycles of length 3 or 4).
Now consider a set of vertices
![]() $A \subseteq V$
of size at most
$A \subseteq V$
of size at most
![]() $n/2$
such that
$n/2$
such that
![]() $G[A]$
(the subgraph of
$G[A]$
(the subgraph of
![]() $G$
induced by
$G$
induced by
![]() $A$
) is connected and
$A$
) is connected and
![]() $x \in A$
. Let
$x \in A$
. Let
![]() $B=\nabla (A)$
and
$B=\nabla (A)$
and
![]() $|B|=|\nabla (A)|=b$
.
$|B|=|\nabla (A)|=b$
.
We then have
![]() $N_I(A)= B\sqcup W$
where
$N_I(A)= B\sqcup W$
where
![]() $W=E(G[A])$
. Note that by summing degrees,
$W=E(G[A])$
. Note that by summing degrees,
![]() $d|A|=b + 2|W|$
, and by the expansion assumption (3) we have
$d|A|=b + 2|W|$
, and by the expansion assumption (3) we have
![]() $b \ge \eta |A|$
. Hence,
$b \ge \eta |A|$
. Hence,
Observe that
![]() $I$
is a subgraph of
$I$
is a subgraph of
![]() $J$
, so
$J$
, so
![]() $N_I(A) \subseteq N_J(A)$
. Let
$N_I(A) \subseteq N_J(A)$
. Let
![]() $B' = N_J(A) \setminus N_I(A)$
. If
$B' = N_J(A) \setminus N_I(A)$
. If
![]() $e \in B'$
, then
$e \in B'$
, then
![]() $e$
must contain the external endpoint of some boundary edge of
$e$
must contain the external endpoint of some boundary edge of
![]() $A$
. There are at most
$A$
. There are at most
![]() $b$
such external endpoints, and each is incident to at most
$b$
such external endpoints, and each is incident to at most
![]() $d-1$
such non-boundary edges. Thus,
$d-1$
such non-boundary edges. Thus,
Let
![]() $A_0 \subseteq A$
be a maximal subset of vertices with pairwise-disjoint neighbourhoods in
$A_0 \subseteq A$
be a maximal subset of vertices with pairwise-disjoint neighbourhoods in
![]() $J$
. We will first determine how many choices there are for
$J$
. We will first determine how many choices there are for
![]() $A_0$
. We claim that
$A_0$
. We claim that
The first inequality holds because the above definitions give
![]() $|N_J(A)| = |B'| + |B| + |W|$
, and each vertex in
$|N_J(A)| = |B'| + |B| + |W|$
, and each vertex in
![]() $A$
has degree at least
$A$
has degree at least
![]() $d^2/2$
in
$d^2/2$
in
![]() $J$
. The second inequality follows from (15) and (16).
$J$
. The second inequality follows from (15) and (16).
The maximality of
![]() $A_0$
gives us that
$A_0$
gives us that
As a result, we have,
Moreover, we make the following claim (where we recall
![]() $x \in A$
is some specified vertex).
$x \in A$
is some specified vertex).
Claim 15.
The set of vertices
![]() $A_0 \cup \{x\}$
is connected in
$A_0 \cup \{x\}$
is connected in
![]() $G^7$
.
$G^7$
.
Proof. We start by proving that
![]() $A_0$
is connected in
$A_0$
is connected in
![]() $G^7$
. Since
$G^7$
. Since
![]() $A$
is connected in
$A$
is connected in
![]() $G$
, and
$G$
, and
![]() $A_0\subseteq A$
, for any pair of distinct vertices
$A_0\subseteq A$
, for any pair of distinct vertices
![]() $u,v\in A_0$
, there must be a path
$u,v\in A_0$
, there must be a path
![]() $P$
from
$P$
from
![]() $u$
to
$u$
to
![]() $v$
along edges of
$v$
along edges of
![]() $G$
using only vertices in
$G$
using only vertices in
![]() $A$
. Let the vertices of
$A$
. Let the vertices of
![]() $P$
be
$P$
be
![]() $w_0 = u, w_1, \dots, w_k = v$
.
$w_0 = u, w_1, \dots, w_k = v$
.
Observe that every vertex in
![]() $P$
is distance at most three in
$P$
is distance at most three in
![]() $G$
from
$G$
from
![]() $A_0$
. This follows from (18); indeed, either
$A_0$
. This follows from (18); indeed, either
![]() $w_i \in A_0$
or there is some
$w_i \in A_0$
or there is some
![]() $u_i \in A_0$
and
$u_i \in A_0$
and
![]() $e \in G$
such that
$e \in G$
such that
![]() $e \in N_J(w_i) \cap N_J(u_i)$
. This means
$e \in N_J(w_i) \cap N_J(u_i)$
. This means
![]() $e$
contains a vertex in
$e$
contains a vertex in
![]() $N_G(w_i)$
and a vertex in
$N_G(w_i)$
and a vertex in
![]() $N_G(u_i)$
. There are three possibilities for
$N_G(u_i)$
. There are three possibilities for
![]() $e$
: either
$e$
: either
![]() $e = u_iv_i$
,
$e = u_iv_i$
,
![]() $e$
is incident to exactly one of
$e$
is incident to exactly one of
![]() $u_i$
or
$u_i$
or
![]() $w_i$
, or
$w_i$
, or
![]() $e$
is incident to neither
$e$
is incident to neither
![]() $u_i$
nor
$u_i$
nor
![]() $w_i$
. These cases give
$w_i$
. These cases give
![]() $\mathrm{dist}_G(w_i, u_i)$
as 1, 2, and 3, respectively. See Fig. 1 for an illustration.
$\mathrm{dist}_G(w_i, u_i)$
as 1, 2, and 3, respectively. See Fig. 1 for an illustration.

Figure 1. The three different cases for an edge
![]() $e$
to be in
$e$
to be in
![]() $N_J(u_i) \cap N_J(w_i)$
.
$N_J(u_i) \cap N_J(w_i)$
.
We can now construct a walk
![]() $P'$
along edges of
$P'$
along edges of
![]() $G$
from
$G$
from
![]() $u$
to
$u$
to
![]() $v$
that visits a vertex in
$v$
that visits a vertex in
![]() $A_0$
at most every seven steps. Let
$A_0$
at most every seven steps. Let
![]() $Q_i$
be a path from
$Q_i$
be a path from
![]() $w_i$
to
$w_i$
to
![]() $A_0$
such that
$A_0$
such that
![]() $|Q_i| \leq 3$
, and let
$|Q_i| \leq 3$
, and let
![]() $Q_i^{-1}$
be the reverse path from
$Q_i^{-1}$
be the reverse path from
![]() $A_0$
to
$A_0$
to
![]() $w_i$
. If
$w_i$
. If
![]() $w_i \in A_0$
, set
$w_i \in A_0$
, set
![]() $Q_i$
and
$Q_i$
and
![]() $Q_i^{-1}$
to be empty. Then the edges of
$Q_i^{-1}$
to be empty. Then the edges of
![]() $P'$
are
$P'$
are
See Fig. 2 for an example. The walk
![]() $P'$
visits vertices of
$P'$
visits vertices of
![]() $A_0$
at most every seven steps, so there is a walk in
$A_0$
at most every seven steps, so there is a walk in
![]() $G^7$
from
$G^7$
from
![]() $u$
to
$u$
to
![]() $v$
using only vertices in
$v$
using only vertices in
![]() $A_0$
. As
$A_0$
. As
![]() $u$
and
$u$
and
![]() $v$
were arbitrary, it follows that
$v$
were arbitrary, it follows that
![]() $A_0$
is connected in
$A_0$
is connected in
![]() $G^7$
.
$G^7$
.

Figure 2. An example of part of the path
![]() $P'$
in red arrows.
$P'$
in red arrows.
This completes the proof of the claim in the case
![]() $x \in A_0$
. If
$x \in A_0$
. If
![]() $x \notin A_0$
, then it is distance at most three in
$x \notin A_0$
, then it is distance at most three in
![]() $G$
from the nearest vertex in
$G$
from the nearest vertex in
![]() $A_0$
and hence is adjacent to a vertex of
$A_0$
and hence is adjacent to a vertex of
![]() $A_0$
in
$A_0$
in
![]() $G^7$
. Thus,
$G^7$
. Thus,
![]() $A_0\cup \{x\}$
is connected in
$A_0\cup \{x\}$
is connected in
![]() $G^7$
as required.
$G^7$
as required.
As a result, we can specify
![]() $A_0$
by specifying a tree of degree at most
$A_0$
by specifying a tree of degree at most
![]() $d^7$
rooted at
$d^7$
rooted at
![]() $v$
(since
$v$
(since
![]() $G^7$
has maximum degree
$G^7$
has maximum degree
![]() $d(d-1)^6\le d^7$
). Using Proposition 14 and the bound on
$d(d-1)^6\le d^7$
). Using Proposition 14 and the bound on
![]() $|A_0|$
given by (17), there are at most
$|A_0|$
given by (17), there are at most
![]() $(ed^7)^{\frac{b}{d}\left (2+\frac{1}{\eta }\right )} = d^{O((1+1/\eta )b/d)}$
possibilities for
$(ed^7)^{\frac{b}{d}\left (2+\frac{1}{\eta }\right )} = d^{O((1+1/\eta )b/d)}$
possibilities for
![]() $A_0$
.
$A_0$
.
We now want to count the number of choices for
![]() $B$
. Let
$B$
. Let
![]() $E_0$
be the edges of
$E_0$
be the edges of
![]() $G$
in
$G$
in
![]() $N^3_J(A_0)$
, meaning the edges which have an endpoint at distance at most 5 from
$N^3_J(A_0)$
, meaning the edges which have an endpoint at distance at most 5 from
![]() $A_0$
, and let
$A_0$
, and let
![]() $G'$
be the graph
$G'$
be the graph
![]() $G$
with every edge in
$G$
with every edge in
![]() $E \setminus E_0$
contracted. By (19) we have that
$E \setminus E_0$
contracted. By (19) we have that
so
![]() $B \subset E(G')$
. We also have
$B \subset E(G')$
. We also have
![]() $v \in V(G')$
if and only if
$v \in V(G')$
if and only if
![]() $\mathrm{dist}_G(u, v) \leq 5$
for some
$\mathrm{dist}_G(u, v) \leq 5$
for some
![]() $u \in A_0$
. Since
$u \in A_0$
. Since
![]() $|N_G^{k-1}(A_0)| \leq (d+1)|N_G^k(A_0)|$
for
$|N_G^{k-1}(A_0)| \leq (d+1)|N_G^k(A_0)|$
for
![]() $k \geq 1$
, this implies
$k \geq 1$
, this implies
![]() $|V(G')| \leq (d+1)^4|A_0| = O(bd^3)$
.
$|V(G')| \leq (d+1)^4|A_0| = O(bd^3)$
.
By (8), the min-cut size of
![]() $G$
is at least
$G$
is at least
![]() $d$
(and in fact exactly
$d$
(and in fact exactly
![]() $d$
since
$d$
since
![]() $G$
is
$G$
is
![]() $d$
-regular). Contracting edges does not decrease the min-cut size of a graph, so the min-cut size of
$d$
-regular). Contracting edges does not decrease the min-cut size of a graph, so the min-cut size of
![]() $G'$
is also at least
$G'$
is also at least
![]() $d$
.
$d$
.
Thus, the number of possible boundaries
![]() $B$
is upper bounded by the number of cuts of size at most
$B$
is upper bounded by the number of cuts of size at most
![]() $b$
in
$b$
in
![]() $G'$
, which by Theorem 13 is at most
$G'$
, which by Theorem 13 is at most
We are done, as we can uniquely determine
![]() $A$
from its boundary.
$A$
from its boundary.
4.2 Colourings with small colour classes: Proof of Lemma 8
Let us now turn to Lemma 8. For a colouring
![]() $\sigma$
, let us use
$\sigma$
, let us use
![]() $\textrm{nm}\!(\sigma ) = \textrm{nm}\!(G,\sigma )$
to denote the number of non-monochromatic edges in
$\textrm{nm}\!(\sigma ) = \textrm{nm}\!(G,\sigma )$
to denote the number of non-monochromatic edges in
![]() $\sigma$
; observe that
$\sigma$
; observe that
![]() $m(G,\sigma ) = |E(G)| - \textrm{nm}\!(\sigma )$
. Recall that
$m(G,\sigma ) = |E(G)| - \textrm{nm}\!(\sigma )$
. Recall that
![]() $S_0$
is the set of colourings in which each colour occupies at most
$S_0$
is the set of colourings in which each colour occupies at most
![]() $n/2$
vertices. The following lemma is the main point of this section.
$n/2$
vertices. The following lemma is the main point of this section.
Lemma 16.
Let
![]() $G$
be as in Theorem 1. For
$G$
be as in Theorem 1. For
![]() $k \geq d$
, let
$k \geq d$
, let
![]() $\mathcal{L}_k$
denote the number of
$\mathcal{L}_k$
denote the number of
![]() $q$
-colorings from
$q$
-colorings from
![]() $S$
which give exactly
$S$
which give exactly
![]() $k$
non-monochromatic edges. Then for
$k$
non-monochromatic edges. Then for
![]() $\delta \gt \frac{12}{\ln d}$
,
$\delta \gt \frac{12}{\ln d}$
,
We would like to briefly comment on parameter
![]() $\delta$
. If one is interested in a combinatorial bound, one could simply plug in the ‘best possible’ value (i.e.,
$\delta$
. If one is interested in a combinatorial bound, one could simply plug in the ‘best possible’ value (i.e.,
![]() $\delta = 12/\ln d$
). We allow for a choice in the parameter
$\delta = 12/\ln d$
). We allow for a choice in the parameter
![]() $\delta$
solely to make the subsequent calculations slightly easier.
$\delta$
solely to make the subsequent calculations slightly easier.
Before using this to prove Lemma 8, we will need the following.
Lemma 17.
Let
![]() $G$
be an
$G$
be an
![]() $\eta$
-expander on
$\eta$
-expander on
![]() $n$
vertices. For every
$n$
vertices. For every
![]() $\sigma \in S_0$
we have
$\sigma \in S_0$
we have
![]() $\textrm{nm}\!(\sigma ) \ge \eta n/2$
.
$\textrm{nm}\!(\sigma ) \ge \eta n/2$
.
Proof. Let
![]() $A_i=\sigma ^{-1}(i)$
be the set of vertices which get colour
$A_i=\sigma ^{-1}(i)$
be the set of vertices which get colour
![]() $i$
under
$i$
under
![]() $\sigma$
, which by the fact that
$\sigma$
, which by the fact that
![]() $\sigma \in S_0$
satisfies
$\sigma \in S_0$
satisfies
![]() $|A_i|\le n/2$
. The non-monochromatic edges of
$|A_i|\le n/2$
. The non-monochromatic edges of
![]() $G$
under
$G$
under
![]() $\sigma$
are precisely those that appear as
$\sigma$
are precisely those that appear as
![]() $\nabla (A_i)$
for two distinct choices of
$\nabla (A_i)$
for two distinct choices of
![]() $i\in [q]$
. This gives
$i\in [q]$
. This gives
We are now ready to prove Lemma 8.
Proof of Lemma
8. We start off with the easy lower bound
![]() $Z_{G}(q,\beta ) \geq q \cdot e^{\beta |E(G)|}$
obtained by considering only the colourings that give every vertex the same colour. So for
$Z_{G}(q,\beta ) \geq q \cdot e^{\beta |E(G)|}$
obtained by considering only the colourings that give every vertex the same colour. So for
![]() $\beta \geq (2+\epsilon )\frac{\ln q}{d}$
, we have
$\beta \geq (2+\epsilon )\frac{\ln q}{d}$
, we have
 \begin{align*} \frac{\sum \limits _{\sigma \in S_0}e^{\beta \left (|E(G)| - \textrm{nm}\!(\sigma )\right )}}{Z_{G}(q,\beta )} &\le \frac{\sum \limits _{k \geq \eta n/2}\sum \limits _{\substack{\sigma \in S_0 \\ \textrm{nm}\!(\sigma ) = k}}e^{\beta (|E(G)| - k)}}{q \cdot e^{\beta |E(G)|}} \\[5pt] & \leq \frac{1}{q}\sum _{k \geq \eta n/2}\sum _{\substack{\sigma \in S_0 \\ \textrm{nm}\!(\sigma ) = k}}q^{-(2+\epsilon )\frac{k}{d}} \\[5pt] & \leq \frac{n^4}{q}\sum _{k \geq \eta n/2}q^{-\Omega \left (\frac{\epsilon k}{d}\right )} \end{align*}
\begin{align*} \frac{\sum \limits _{\sigma \in S_0}e^{\beta \left (|E(G)| - \textrm{nm}\!(\sigma )\right )}}{Z_{G}(q,\beta )} &\le \frac{\sum \limits _{k \geq \eta n/2}\sum \limits _{\substack{\sigma \in S_0 \\ \textrm{nm}\!(\sigma ) = k}}e^{\beta (|E(G)| - k)}}{q \cdot e^{\beta |E(G)|}} \\[5pt] & \leq \frac{1}{q}\sum _{k \geq \eta n/2}\sum _{\substack{\sigma \in S_0 \\ \textrm{nm}\!(\sigma ) = k}}q^{-(2+\epsilon )\frac{k}{d}} \\[5pt] & \leq \frac{n^4}{q}\sum _{k \geq \eta n/2}q^{-\Omega \left (\frac{\epsilon k}{d}\right )} \end{align*}
where the first inequality uses Lemma 17 and the last inequality uses Lemma 16 with
![]() $\delta = \epsilon$
(note that we already assume that
$\delta = \epsilon$
(note that we already assume that
![]() $d \geq \exp \left (\Omega (1/\epsilon )\right )$
). If
$d \geq \exp \left (\Omega (1/\epsilon )\right )$
). If
![]() $d \geq \sqrt{n}$
, then
$d \geq \sqrt{n}$
, then
![]() $\frac{n^4}{q} \lt 1$
. Otherwise,
$\frac{n^4}{q} \lt 1$
. Otherwise,
![]() $n^4 = q^{o\left (\frac{\epsilon k}{d}\right )}$
. In either case,
$n^4 = q^{o\left (\frac{\epsilon k}{d}\right )}$
. In either case,
 \begin{equation*} \frac {n^4}{q}\sum _{k \geq \eta n/2}q^{-\Omega \left (\frac {\epsilon k}{d}\right )} \leq q^{-\Omega \left (\frac {\epsilon n}{d}\right )}. \end{equation*}
\begin{equation*} \frac {n^4}{q}\sum _{k \geq \eta n/2}q^{-\Omega \left (\frac {\epsilon k}{d}\right )} \leq q^{-\Omega \left (\frac {\epsilon n}{d}\right )}. \end{equation*}
One ingredient in the proof of Lemma 16 is the following, which requires the same techniques as in the proof of Theorem 13.
Lemma 18.
Let
![]() $G$
be as in Theorem 1. Let
$G$
be as in Theorem 1. Let
![]() $\mathcal{C}(\ell, s)$
be the number of
$\mathcal{C}(\ell, s)$
be the number of
![]() $q$
-colorings of the vertices of
$q$
-colorings of the vertices of
![]() $G$
such that there are exactly
$G$
such that there are exactly
![]() $\ell$
non-monochromatic edges, where each monochromatic component has at least
$\ell$
non-monochromatic edges, where each monochromatic component has at least
![]() $s$
vertices. Then we have
$s$
vertices. Then we have
-
(1)
 $\mathcal{C}(\ell,1) \leq \binom{n}{2\ell/d}q^{\frac{2\ell }{d}}$
, and
$\mathcal{C}(\ell,1) \leq \binom{n}{2\ell/d}q^{\frac{2\ell }{d}}$
, and
-
(2)
 $\mathcal{C}(\ell,2) \leq \binom{n}{2\ell/d}q^{\frac{2\ell }{2d - 2}}\cdot (2d)^{\frac{2\ell }{d}}$
.
$\mathcal{C}(\ell,2) \leq \binom{n}{2\ell/d}q^{\frac{2\ell }{2d - 2}}\cdot (2d)^{\frac{2\ell }{d}}$
.
Proof. For part 1: Fix any
![]() $q$
-coloring
$q$
-coloring
![]() $\sigma$
with exactly
$\sigma$
with exactly
![]() $\ell$
non-monochromatic edges and run the following algorithm on
$\ell$
non-monochromatic edges and run the following algorithm on
![]() $G$
.
$G$
.
-
I. While there are more than
 $\frac{2\ell }{d}$
vertices, choose a uniformly random edge and contract it. Delete self-loops, if any, after each contraction.
$\frac{2\ell }{d}$
vertices, choose a uniformly random edge and contract it. Delete self-loops, if any, after each contraction. -
II. Colour every vertex uniformly and independently from
 $[q]$
. Output the final graph
$[q]$
. Output the final graph
 $G'$
and colouring
$G'$
and colouring
 $\sigma '$
.
$\sigma '$
.
Observe that
![]() $\sigma '$
naturally corresponds to a
$\sigma '$
naturally corresponds to a
![]() $q$
-coloring
$q$
-coloring
![]() $\sigma$
in the original graph defined by
$\sigma$
in the original graph defined by
![]() $\sigma (v) = \sigma '(v')$
where
$\sigma (v) = \sigma '(v')$
where
![]() $v'$
is the vertex in
$v'$
is the vertex in
![]() $G'$
into which
$G'$
into which
![]() $v$
was contracted.
$v$
was contracted.
Recall that
![]() $G$
has a min-cut of size
$G$
has a min-cut of size
![]() $d$
by (8), and it does not decrease with the contraction operation during step I. So at any point in this step, if the current graph has
$d$
by (8), and it does not decrease with the contraction operation during step I. So at any point in this step, if the current graph has
![]() $m$
vertices, then it has at least
$m$
vertices, then it has at least
![]() $\frac{md}{2}$
edges.
$\frac{md}{2}$
edges.
Moreover, each contraction reduces the number of vertices by
![]() $1$
, and all deleted self-loops must be monochromatic. So the probability that the
$1$
, and all deleted self-loops must be monochromatic. So the probability that the
![]() $\ell$
non-monochromatic edges remain uncontracted in
$\ell$
non-monochromatic edges remain uncontracted in
![]() $G'$
is at least
$G'$
is at least
During step II, the probability that every contracted vertex gets the correct colour is
![]() $q^{-\frac{2\ell }{d}}$
. Therefore, the probability that
$q^{-\frac{2\ell }{d}}$
. Therefore, the probability that
![]() $\sigma$
was recovered by this procedure is at least
$\sigma$
was recovered by this procedure is at least
![]() $\binom{n}{2\ell/d}^{-1}q^{-\frac{2\ell }{d}}$
. Since this holds for any
$\binom{n}{2\ell/d}^{-1}q^{-\frac{2\ell }{d}}$
. Since this holds for any
![]() $\sigma$
, there are at most
$\sigma$
, there are at most
![]() $\binom{n}{2\ell/d}q^{\frac{2\ell }{d}}$
many
$\binom{n}{2\ell/d}q^{\frac{2\ell }{d}}$
many
![]() $q$
-colorings with
$q$
-colorings with
![]() $\ell$
non-monochromatic edges.
$\ell$
non-monochromatic edges.
For part 2: Fix any
![]() $q$
-coloring
$q$
-coloring
![]() $\sigma$
with at least
$\sigma$
with at least
![]() $\ell$
non-monochromatic edges where each monochromatic component has at least
$\ell$
non-monochromatic edges where each monochromatic component has at least
![]() $2$
vertices, and consider the following algorithm.
$2$
vertices, and consider the following algorithm.
-
I. While there are more than
 $\frac{2\ell }{d}$
vertices, choose a uniformly random edge and contract it. Delete self-loops, if any, after each contraction.
$\frac{2\ell }{d}$
vertices, choose a uniformly random edge and contract it. Delete self-loops, if any, after each contraction. -
II. While a vertex in this contracted graph has degree
 $d$
, contract it with one of its neighbours uniformly at random, deleting self-loops at each stage.
$d$
, contract it with one of its neighbours uniformly at random, deleting self-loops at each stage. -
III. While there are more than
 $\frac{2\ell }{2d - 2}$
vertices, choose a uniformly random edge and contract it. Delete self-loops, if any, after each contraction.
$\frac{2\ell }{2d - 2}$
vertices, choose a uniformly random edge and contract it. Delete self-loops, if any, after each contraction. -
IV. Colour every vertex uniformly and independently at random from
 $[q]$
.
$[q]$
.
Again, the final colouring naturally corresponds to a
![]() $q$
-coloring in
$q$
-coloring in
![]() $G$
. Step I is analysed in an identical manner as
$G$
. Step I is analysed in an identical manner as
![]() $(1)$
. The probability that the
$(1)$
. The probability that the
![]() $\ell$
non-monochromatic edges remain uncontracted at the end of this step is at least
$\ell$
non-monochromatic edges remain uncontracted at the end of this step is at least
![]() $\binom{n}{2\ell/d}^{-1}$
.
$\binom{n}{2\ell/d}^{-1}$
.
Since every monochromatic component in
![]() $\sigma$
has at least two vertices, every uncontracted vertex at the end of step I is incident to at least one monochromatic edge. So during step II, the probability that the
$\sigma$
has at least two vertices, every uncontracted vertex at the end of step I is incident to at least one monochromatic edge. So during step II, the probability that the
![]() $\ell$
non-monochromatic edges remain uncontracted is at most
$\ell$
non-monochromatic edges remain uncontracted is at most
![]() $d^{-\frac{2\ell }{d}}$
.
$d^{-\frac{2\ell }{d}}$
.
After the end of step II, (7) guarantees that the min-cut is at least
![]() $2d-2$
, and this does not decrease with the contraction operation in step III. So, using a calculation similar to that in the analysis of step I, the probability that the
$2d-2$
, and this does not decrease with the contraction operation in step III. So, using a calculation similar to that in the analysis of step I, the probability that the
![]() $\ell$
non-monochromatic edges remain uncontracted at the end of this step is at least
$\ell$
non-monochromatic edges remain uncontracted at the end of this step is at least
![]() $2^{-\frac{2\ell }{d}}$
.
$2^{-\frac{2\ell }{d}}$
.
During step IV, the probability that every contracted vertex gets the correct colour is
![]() $q^{-\frac{2\ell }{2d-2}}$
. Thus,
$q^{-\frac{2\ell }{2d-2}}$
. Thus,
![]() $\sigma$
is recovered with probability at least
$\sigma$
is recovered with probability at least
![]() $\binom{n}{2\ell/d}^{-1}q^{-\frac{2\ell }{(2d-2)}}(2d)^{-\frac{2\ell }{d}}$
. Since this holds for any
$\binom{n}{2\ell/d}^{-1}q^{-\frac{2\ell }{(2d-2)}}(2d)^{-\frac{2\ell }{d}}$
. Since this holds for any
![]() $\sigma$
, we have that there are at most
$\sigma$
, we have that there are at most
![]() $\binom{n}{2\ell/d}q^{\frac{2\ell }{(2d-2)}}(2d)^{\frac{2\ell }{d}}$
many
$\binom{n}{2\ell/d}q^{\frac{2\ell }{(2d-2)}}(2d)^{\frac{2\ell }{d}}$
many
![]() $q$
-colorings with
$q$
-colorings with
![]() $\ell$
non-monochromatic edges and each monochromatic component having size at least
$\ell$
non-monochromatic edges and each monochromatic component having size at least
![]() $2$
.
$2$
.
One can check by hand that our bound is not tight in several cases, such as when
![]() $s = 1$
and
$s = 1$
and
![]() $\ell = d$
. Indeed, the original algorithm by Karger for min-cuts gives a reasonable tight lower bound on the number of near-minimum cuts when
$\ell = d$
. Indeed, the original algorithm by Karger for min-cuts gives a reasonable tight lower bound on the number of near-minimum cuts when
![]() $G$
is a cycle – a case that is not included in the class of graphs under consideration for Theorem 1. However, recent work obtaining a more fine-grained understanding of the Karger process may be adaptable to our setting of
$G$
is a cycle – a case that is not included in the class of graphs under consideration for Theorem 1. However, recent work obtaining a more fine-grained understanding of the Karger process may be adaptable to our setting of
![]() $q$
-colorings; we refer the interested reader to [Reference Gupta, Harris, Lee and Li15].
$q$
-colorings; we refer the interested reader to [Reference Gupta, Harris, Lee and Li15].
We are now ready to prove Lemma 16. Recall that
![]() $\mathcal{L}_k$
is the number of
$\mathcal{L}_k$
is the number of
![]() $q$
-colorings from
$q$
-colorings from
![]() $S_0$
which induce exactly
$S_0$
which induce exactly
![]() $k$
non-monochromatic edges, and we want to show that
$k$
non-monochromatic edges, and we want to show that
Proof of Lemma
16. Case 1:
![]() $k \leq nd^{1 - \frac{\delta }{4}}$
. For a subset
$k \leq nd^{1 - \frac{\delta }{4}}$
. For a subset
![]() $A \subset V$
, let
$A \subset V$
, let
![]() $E(A)$
denote the set of edges induced by
$E(A)$
denote the set of edges induced by
![]() $A$
. Consider a partition of the vertices of
$A$
. Consider a partition of the vertices of
![]() $G$
into
$G$
into
![]() $L$
monochromatic components. Let
$L$
monochromatic components. Let
![]() $T$
be the set of components containing exactly one vertex. Let
$T$
be the set of components containing exactly one vertex. Let
![]() $N$
be the set of non-monochromatic edges. We then have the partition
$N$
be the set of non-monochromatic edges. We then have the partition
Let
![]() $e_T \,{:\!=}\, |E(T)|$
,
$e_T \,{:\!=}\, |E(T)|$
,
![]() $b_T \,{:\!=}\, |\nabla (T)|$
, and
$b_T \,{:\!=}\, |\nabla (T)|$
, and
![]() $\ell \,{:\!=}\, \left |N\cap E (\overline{T})\right | = k - e_T - b_T$
. We have that
$\ell \,{:\!=}\, \left |N\cap E (\overline{T})\right | = k - e_T - b_T$
. We have that
![]() $|T| \leq \frac{2k}{d} \leq nd^{-\delta } \lt n/3$
and each monochromatic component has size at most
$|T| \leq \frac{2k}{d} \leq nd^{-\delta } \lt n/3$
and each monochromatic component has size at most
![]() $n/2$
. So, one can choose some
$n/2$
. So, one can choose some
![]() $S \subseteq V$
such that
$S \subseteq V$
such that
![]() $n/3 \leq |S|\leq 2n/3$
by greedily including all vertices from the smallest remaining monochromatic component. In particular,
$n/3 \leq |S|\leq 2n/3$
by greedily including all vertices from the smallest remaining monochromatic component. In particular,
![]() $S \supseteq T$
. The expansion condition (3) then implies that
$S \supseteq T$
. The expansion condition (3) then implies that
![]() $|\nabla (S)| \geq n/3$
. However,
$|\nabla (S)| \geq n/3$
. However,
![]() $\nabla (S) \subseteq \nabla (T) \cup (N \cap E(\overline{T}))$
, and so
$\nabla (S) \subseteq \nabla (T) \cup (N \cap E(\overline{T}))$
, and so
![]() $|\nabla (S)| \leq b_T + (k - e_T - b_T) = k - e_T = \ell + b_T$
. As a result, we have
$|\nabla (S)| \leq b_T + (k - e_T - b_T) = k - e_T = \ell + b_T$
. As a result, we have
A
![]() $q$
-coloring counted by
$q$
-coloring counted by
![]() $\mathcal{L}_k$
can be chosen by (I) first choosing the cut
$\mathcal{L}_k$
can be chosen by (I) first choosing the cut
![]() $\left (T, \overline{T}\right )$
, (II) giving each element on the
$\left (T, \overline{T}\right )$
, (II) giving each element on the
![]() $T$
-side of the cut a colour, and (III) choosing the monochromatic components in
$T$
-side of the cut a colour, and (III) choosing the monochromatic components in
![]() $V \setminus T$
so that each component has at least two vertices.
$V \setminus T$
so that each component has at least two vertices.
Theorem 13 gives us that (I) can be done in at most
![]() $\binom{n}{2b_T/d} \cdot 2^{2b_T/d}$
ways. We also have that (II) can be done in at most
$\binom{n}{2b_T/d} \cdot 2^{2b_T/d}$
ways. We also have that (II) can be done in at most
![]() $q^{|T|}$
ways. Part 2 of Lemma 18 gives us that (III) can be done in at most
$q^{|T|}$
ways. Part 2 of Lemma 18 gives us that (III) can be done in at most
![]() $\binom{n}{2\ell/d}\cdot q^{\frac{2\ell }{2d-2}}\cdot (2d)^{\frac{2\ell }{d}}$
ways. So, the number of
$\binom{n}{2\ell/d}\cdot q^{\frac{2\ell }{2d-2}}\cdot (2d)^{\frac{2\ell }{d}}$
ways. So, the number of
![]() $q$
-colorings of
$q$
-colorings of
![]() $V$
with the above parameters is at most
$V$
with the above parameters is at most
 \begin{align*} Q & \,{:\!=}\,\binom{n}{2b_T/d} \cdot 2^{2b_T/d} \cdot q^{|T|} \cdot \binom{n}{2\ell/d}\cdot q^{\frac{2\ell }{2d-2}} \cdot (2d)^{\frac{2\ell }{d}} \\[5pt] & = \binom{n}{2b_T/d}\cdot \binom{n}{2\ell/d}\cdot q^{\frac{\ell + 2e_T + b_T}{d}} \cdot q^{\frac{\ell }{d^2}} \cdot (2d)^{\frac{2\ell }{d}}, \\[5pt] \end{align*}
\begin{align*} Q & \,{:\!=}\,\binom{n}{2b_T/d} \cdot 2^{2b_T/d} \cdot q^{|T|} \cdot \binom{n}{2\ell/d}\cdot q^{\frac{2\ell }{2d-2}} \cdot (2d)^{\frac{2\ell }{d}} \\[5pt] & = \binom{n}{2b_T/d}\cdot \binom{n}{2\ell/d}\cdot q^{\frac{\ell + 2e_T + b_T}{d}} \cdot q^{\frac{\ell }{d^2}} \cdot (2d)^{\frac{2\ell }{d}}, \\[5pt] \end{align*}
where we have used
![]() $d|T| = 2e_T + b_T$
. So we have
$d|T| = 2e_T + b_T$
. So we have
 \begin{align*} Q \cdot q^{-\frac{2k}{d}} & = \binom{n}{2\ell/d}\binom{n}{2b_T/d}\cdot q^{\frac{-b_T - \ell }{d}} \cdot q^{\frac{\ell }{d^2}}\cdot (2d)^{\frac{2\ell }{d}} \\[5pt] & \leq \binom{n}{2(\ell + b_T)/d} \cdot 2^{\frac{4(b_T + \ell )}{d}} q^{\frac{-b_T - \ell }{d}} \cdot q^{\frac{\ell }{d^2}} \cdot (2d)^{\frac{2\ell }{d}} \\[5pt] & \leq d^{O\left (\frac{\ell + b_T}{d}\right )}q^{-\frac{\ell + b_T}{d}} \cdot 2^{\frac{4(b_T + \ell )}{d}}q^{\frac{\ell }{d^2}} \\[5pt] & \leq q^{-\Omega \left (\frac{n}{d}\right )}, \end{align*}
\begin{align*} Q \cdot q^{-\frac{2k}{d}} & = \binom{n}{2\ell/d}\binom{n}{2b_T/d}\cdot q^{\frac{-b_T - \ell }{d}} \cdot q^{\frac{\ell }{d^2}}\cdot (2d)^{\frac{2\ell }{d}} \\[5pt] & \leq \binom{n}{2(\ell + b_T)/d} \cdot 2^{\frac{4(b_T + \ell )}{d}} q^{\frac{-b_T - \ell }{d}} \cdot q^{\frac{\ell }{d^2}} \cdot (2d)^{\frac{2\ell }{d}} \\[5pt] & \leq d^{O\left (\frac{\ell + b_T}{d}\right )}q^{-\frac{\ell + b_T}{d}} \cdot 2^{\frac{4(b_T + \ell )}{d}}q^{\frac{\ell }{d^2}} \\[5pt] & \leq q^{-\Omega \left (\frac{n}{d}\right )}, \end{align*}
where the first inequality used the fact that for
![]() $a+b \leq x$
, we have
$a+b \leq x$
, we have
![]() $\binom{x}{a}\binom{x}{b} \leq \binom{x}{a+b}4^{a+b}$
, and the next two inequalities use (20). So summing over all values for
$\binom{x}{a}\binom{x}{b} \leq \binom{x}{a+b}4^{a+b}$
, and the next two inequalities use (20). So summing over all values for
![]() $\ell$
and
$\ell$
and
![]() $b_T$
gives us that for
$b_T$
gives us that for
![]() $k \leq nd^{1 - \frac{\delta }{4}}$
,
$k \leq nd^{1 - \frac{\delta }{4}}$
,
Case 2:
![]() $k \geq nd^{1 - \frac{\delta }{4}}$
. This case is relatively straightforward. Using part 1 of Lemma 18, we have
$k \geq nd^{1 - \frac{\delta }{4}}$
. This case is relatively straightforward. Using part 1 of Lemma 18, we have
5. Extremal results for partition functions
An important step in upper bounding the weight
![]() $w_\gamma = e^{-\beta (\nabla _\gamma + e_\gamma )}Z_{\gamma }(q-1,\beta )$
is to upper bound the partition function
$w_\gamma = e^{-\beta (\nabla _\gamma + e_\gamma )}Z_{\gamma }(q-1,\beta )$
is to upper bound the partition function
![]() $Z_{\gamma }(q-1,\beta )$
. Bounds on partition functions in this setting are a well-studied topic in extremal combinatorics.
$Z_{\gamma }(q-1,\beta )$
. Bounds on partition functions in this setting are a well-studied topic in extremal combinatorics.
5.1 General graphs and cliques
Theorem 19 (Sah et al. [Reference Sah, Sawhney, Stoner and Zhao40], Theorem 1.14 restated). Let
![]() $G$
be a graph,
$G$
be a graph,
![]() $q\ge 2$
be an integer and
$q\ge 2$
be an integer and
![]() $\beta \ge 0$
. Then
$\beta \ge 0$
. Then
where
![]() $d_v$
is the degree of a vertex
$d_v$
is the degree of a vertex
![]() $v\in V(G)$
.
$v\in V(G)$
.
We briefly remark that their result was much more general; [Reference Sah, Sawhney, Stoner and Zhao40] shows that in fact every ferromagnetic model (using a definition introduced in [Reference Galanis, Štefankovič and Vigoda18] as a generalisation of the ferromagnetic Potts model) is ‘clique-maximizing’, which translates to the above statement on the level of partition functions.
Corollary 20.
Let
![]() $G$
be a graph of maximum degree
$G$
be a graph of maximum degree
![]() $\Delta$
with
$\Delta$
with
![]() $n$
vertices and
$n$
vertices and
![]() $m$
edges. Then for any integer
$m$
edges. Then for any integer
![]() $q\ge 2$
and
$q\ge 2$
and
![]() $\beta \ge 0$
,
$\beta \ge 0$
,
Proof. This follows from Theorem 19 and the fact that
![]() $Z_{K_{d+1}}(q,\beta )^{\frac{1}{d+1}}$
forms a log-convex sequence for
$Z_{K_{d+1}}(q,\beta )^{\frac{1}{d+1}}$
forms a log-convex sequence for
![]() $d\ge 0$
, which is proved in ([Reference Sah, Sawhney, Stoner and Zhao40], Lemma 5.3). In particular, consider the graph with partition function
$d\ge 0$
, which is proved in ([Reference Sah, Sawhney, Stoner and Zhao40], Lemma 5.3). In particular, consider the graph with partition function
![]() $Z_G(q,\beta )^\Delta$
formed from the disjoint union of
$Z_G(q,\beta )^\Delta$
formed from the disjoint union of
![]() $\Delta$
copies of
$\Delta$
copies of
![]() $G$
. Applying Theorem 19, we obtain an upper bound on
$G$
. Applying Theorem 19, we obtain an upper bound on
![]() $Z_G(q,\beta )^\Delta$
in terms of a degree sequence. We can further increase the upper bound because the aforementioned log-convexity implies that when
$Z_G(q,\beta )^\Delta$
in terms of a degree sequence. We can further increase the upper bound because the aforementioned log-convexity implies that when
![]() $a\le b$
, replacing two degrees
$a\le b$
, replacing two degrees
![]() $a$
and
$a$
and
![]() $b$
by degrees
$b$
by degrees
![]() $a-1$
and
$a-1$
and
![]() $b+1$
can only increase the bound. Then over graphs of maximum degree
$b+1$
can only increase the bound. Then over graphs of maximum degree
![]() $\Delta$
with
$\Delta$
with
![]() $\Delta n$
vertices and
$\Delta n$
vertices and
![]() $\Delta m$
edges, the maximum upper bound Theorem 19 can give is from a degree sequence where
$\Delta m$
edges, the maximum upper bound Theorem 19 can give is from a degree sequence where
![]() $2m$
vertices have degree
$2m$
vertices have degree
![]() $\Delta$
and the rest have degree zero. The result follows upon taking the power
$\Delta$
and the rest have degree zero. The result follows upon taking the power
![]() $1/\Delta$
of this inequality.
$1/\Delta$
of this inequality.
5.2 Triangle-free graphs and bicliques
The upper bound in Theorem 19 can be improved in the case that
![]() $G$
is triangle-free.
$G$
is triangle-free.
Theorem 21 (Sah et al. [Reference Sah, Sawhney, Stoner and Zhao40], Theorem 1.9 and the subsequent remark). Let
![]() $G$
be a triangle-free graph with no isolated vertices,
$G$
be a triangle-free graph with no isolated vertices,
![]() $q\ge 2$
be an integer and
$q\ge 2$
be an integer and
![]() $\beta \ge 0$
. Then
$\beta \ge 0$
. Then
where
![]() $d_u$
is the degree of a vertex
$d_u$
is the degree of a vertex
![]() $u\in V(G)$
.
$u\in V(G)$
.
Corollary 22.
Let
![]() $G$
be a triangle-free graph of maximum degree
$G$
be a triangle-free graph of maximum degree
![]() $\Delta$
with
$\Delta$
with
![]() $n$
vertices and
$n$
vertices and
![]() $m$
edges. Then for any integer
$m$
edges. Then for any integer
![]() $q\ge 2$
and
$q\ge 2$
and
![]() $\beta \ge 0$
,
$\beta \ge 0$
,
Proof. Let
![]() $G$
have
$G$
have
![]() $t$
isolated vertices. Then by Theorem 21 we have
$t$
isolated vertices. Then by Theorem 21 we have
The desired result is now a consequence of the fact that for
![]() $1\le a\le c$
and
$1\le a\le c$
and
![]() $1\le b\le d$
we have
$1\le b\le d$
we have
To see this, apply the inequality to each term of the product and collect the factors of
![]() $q$
to obtain
$q$
to obtain
Some simple counting gives
 \begin{equation*} \sum _{uv\in E(G)}\left (\frac {1}{d_u}+\frac {1}{d_v}\right ) = n - t \end{equation*}
\begin{equation*} \sum _{uv\in E(G)}\left (\frac {1}{d_u}+\frac {1}{d_v}\right ) = n - t \end{equation*}
since each vertex
![]() $u$
appears as the endpoint of precisely
$u$
appears as the endpoint of precisely
![]() $d_u$
edges, and the result follows.
$d_u$
edges, and the result follows.
It remains to prove inequality (21), which follows from Hölder’s inequality and Jensen’s inequality as notedFootnote 2 in [Reference Sah, Sawhney, Stoner and Zhao40]. For concreteness, we observe that inequality (21) is a direct consequence of a generalised Hölder inequality stated as Theorem 3.1 in [Reference Lubetzky and Zhao32]. We can write
![]() $\Omega =[q]$
, and let
$\Omega =[q]$
, and let
![]() $\mu$
be the uniform probability measure on
$\mu$
be the uniform probability measure on
![]() $\Omega$
and
$\Omega$
and
![]() $\mu ^a$
be the uniform probability measure on
$\mu ^a$
be the uniform probability measure on
![]() $\Omega ^a$
such that for the non-negative functions
$\Omega ^a$
such that for the non-negative functions
![]() $f\,{:}\,\Omega ^2\to \mathbb{R}$
and
$f\,{:}\,\Omega ^2\to \mathbb{R}$
and
![]() $g\,{:}\,\Omega ^a\to \mathbb{R}$
given by
$g\,{:}\,\Omega ^a\to \mathbb{R}$
given by
 \begin{align*} f(x,y) &= \begin{cases}e^\beta & x = y \\[5pt] 1 & \text{otherwise},\end{cases} \\[5pt] g(x_1,\dotsc,x_a) &= \int _{\Omega } \prod _{i=1}^a f(x_i,y) \,\mathrm d\mu. \end{align*}
\begin{align*} f(x,y) &= \begin{cases}e^\beta & x = y \\[5pt] 1 & \text{otherwise},\end{cases} \\[5pt] g(x_1,\dotsc,x_a) &= \int _{\Omega } \prod _{i=1}^a f(x_i,y) \,\mathrm d\mu. \end{align*}
Then to prove (21) in this notation, we have
 \begin{equation*} \mathrm {LHS} \,{:\!=}\, q^{-\left (\frac {1}{a}+\frac {1}{b}\right )} Z_{K_{a, b}}(q,\beta )^{\frac {1}{a b}} = \left (\int _{[q]^a}|g|^b\,\mathrm d\mu ^a\right )^{\frac {1}{ab}}. \end{equation*}
\begin{equation*} \mathrm {LHS} \,{:\!=}\, q^{-\left (\frac {1}{a}+\frac {1}{b}\right )} Z_{K_{a, b}}(q,\beta )^{\frac {1}{a b}} = \left (\int _{[q]^a}|g|^b\,\mathrm d\mu ^a\right )^{\frac {1}{ab}}. \end{equation*}
When
![]() $b\le d$
we can apply the generalised Hölder inequality (or in this somewhat special case iterated applications of the usual Hölder inequality followed by Jensen’s inequality) to the integral over
$b\le d$
we can apply the generalised Hölder inequality (or in this somewhat special case iterated applications of the usual Hölder inequality followed by Jensen’s inequality) to the integral over
![]() $[q]^a$
above to obtain the upper bound
$[q]^a$
above to obtain the upper bound
A symmetric application of this argument for any integer
![]() $c$
such that
$c$
such that
![]() $a\le c$
gives inequality (21).
$a\le c$
gives inequality (21).
Lemma 23.
Let
![]() $q \geq d^{4}$
and for some fixed
$q \geq d^{4}$
and for some fixed
![]() $\epsilon \gt 0$
let
$\epsilon \gt 0$
let
![]() $\beta \ge (1+\epsilon )\beta _o$
. Then,
$\beta \ge (1+\epsilon )\beta _o$
. Then,
-
(1)
 $Z_{K_{d+1}}(q,\beta ) \le (1+q^{-\Omega (\epsilon )})q e^{\beta \binom{d+1}{2}}$
, and
$Z_{K_{d+1}}(q,\beta ) \le (1+q^{-\Omega (\epsilon )})q e^{\beta \binom{d+1}{2}}$
, and
-
(2)
 $Z_{K_{d,d}}(q,\beta ) \le (1+ q^{-\Omega (\epsilon )})qe^{\beta d^2}$
.
$Z_{K_{d,d}}(q,\beta ) \le (1+ q^{-\Omega (\epsilon )})qe^{\beta d^2}$
.
Proof. We will use the fact that both
![]() $K_{d+1}$
and
$K_{d+1}$
and
![]() $K_{d,d}$
are
$K_{d,d}$
are
![]() $\eta$
-expanders with
$\eta$
-expanders with
![]() $\eta = d/2$
. We will state the proof for
$\eta = d/2$
. We will state the proof for
![]() $K_{d+1}$
, and proof for
$K_{d+1}$
, and proof for
![]() $K_{d,d}$
follows similarly. Let
$K_{d,d}$
follows similarly. Let
![]() $\sigma$
be any colouring of the vertices of
$\sigma$
be any colouring of the vertices of
![]() $K_d$
, and let
$K_d$
, and let
![]() $c(\sigma )$
denote the number of colours that appear in
$c(\sigma )$
denote the number of colours that appear in
![]() $\sigma$
.
$\sigma$
.
We first observe that the proof of Lemma 16 also extends to all
![]() $\sigma$
such that
$\sigma$
such that
![]() $c(\sigma ) \geq 2$
. Indeed, the only place where
$c(\sigma ) \geq 2$
. Indeed, the only place where
![]() $S$
was used was to establish Lemma 17, and (20). Both of these also hold for
$S$
was used was to establish Lemma 17, and (20). Both of these also hold for
![]() $K_{d+1}$
whenever there are at least two colours. So we have
$K_{d+1}$
whenever there are at least two colours. So we have
 \begin{align*} \frac{\sum _{\sigma :c(\sigma ) \geq 2}e^{\beta \left (\binom{d+1}{2} - \textrm{nm}\!(\sigma )\right )}}{q \cdot e^{\beta \binom{d+1}{2}}} & \leq \frac{1}{q}\sum _{k \geq d}\sum _{\substack{\sigma :c(\sigma ) \geq 2 \\ \textrm{nm}\!(\sigma ) = k}}q^{-(2+\epsilon )\frac{k}{d}} \\[5pt] & \leq \frac{d^4}{q}\sum _{k \geq d}q^{-\Omega \left (\frac{\epsilon k}{d}\right )} \\[5pt] & \leq q^{-\Omega \left (\epsilon \right )}. \end{align*}
\begin{align*} \frac{\sum _{\sigma :c(\sigma ) \geq 2}e^{\beta \left (\binom{d+1}{2} - \textrm{nm}\!(\sigma )\right )}}{q \cdot e^{\beta \binom{d+1}{2}}} & \leq \frac{1}{q}\sum _{k \geq d}\sum _{\substack{\sigma :c(\sigma ) \geq 2 \\ \textrm{nm}\!(\sigma ) = k}}q^{-(2+\epsilon )\frac{k}{d}} \\[5pt] & \leq \frac{d^4}{q}\sum _{k \geq d}q^{-\Omega \left (\frac{\epsilon k}{d}\right )} \\[5pt] & \leq q^{-\Omega \left (\epsilon \right )}. \end{align*}
The proofs of Lemmas 11 and 12 are now straightforward calculations.
Proof of Lemma 11. By Corollary 20 and Lemma 23,
 \begin{align*} Z_{G[\gamma ]}(q-1, \beta ) &\leq (q-1)^{v_\gamma -\frac{2e_\gamma }{d}} Z_{K_{d+1}}(q-1, \beta )^{\frac{2e_\gamma }{d(d+1)}}\\[5pt] &\leq (q-1)^{v_\gamma -\frac{2e_\gamma }{d}}\left (2(q-1) e^{\beta \binom{d+1}{2}}\right )^{\frac{2e_\gamma }{d(d+1)}}\\[5pt] &\lt q^{v_\gamma - \frac{2e_\gamma }{d}+\frac{e_\gamma }{\binom{d+1}{2}}} e^{\beta e_\gamma }2^{\frac{e_\gamma }{\binom{d+1}{2}}}. \end{align*}
\begin{align*} Z_{G[\gamma ]}(q-1, \beta ) &\leq (q-1)^{v_\gamma -\frac{2e_\gamma }{d}} Z_{K_{d+1}}(q-1, \beta )^{\frac{2e_\gamma }{d(d+1)}}\\[5pt] &\leq (q-1)^{v_\gamma -\frac{2e_\gamma }{d}}\left (2(q-1) e^{\beta \binom{d+1}{2}}\right )^{\frac{2e_\gamma }{d(d+1)}}\\[5pt] &\lt q^{v_\gamma - \frac{2e_\gamma }{d}+\frac{e_\gamma }{\binom{d+1}{2}}} e^{\beta e_\gamma }2^{\frac{e_\gamma }{\binom{d+1}{2}}}. \end{align*}
Proof of Lemma 12. By Corollary 22 and Lemma 23,
 \begin{align*} Z_{G[\gamma ]}(q-1, \beta )&\leq (q-1)^{v_\gamma - \frac{2e_\gamma }{d}}Z_{K_{d,d}}(q-1,\beta )^{\frac{e_\gamma }{d^2}}\\[5pt] &\leq (q-1)^{v_\gamma - \frac{2e_\gamma }{d}} \cdot (2(q-1)e^{\beta d^2})^{\frac{e_\gamma }{d^2}}\\[5pt] &\leq q^{v_\gamma - \frac{2e_\gamma }{d}+\frac{e_\gamma }{d^2}} \cdot 2^{\frac{e_\gamma }{d^2}} \cdot e^{\beta e_\gamma }. \end{align*}
\begin{align*} Z_{G[\gamma ]}(q-1, \beta )&\leq (q-1)^{v_\gamma - \frac{2e_\gamma }{d}}Z_{K_{d,d}}(q-1,\beta )^{\frac{e_\gamma }{d^2}}\\[5pt] &\leq (q-1)^{v_\gamma - \frac{2e_\gamma }{d}} \cdot (2(q-1)e^{\beta d^2})^{\frac{e_\gamma }{d^2}}\\[5pt] &\leq q^{v_\gamma - \frac{2e_\gamma }{d}+\frac{e_\gamma }{d^2}} \cdot 2^{\frac{e_\gamma }{d^2}} \cdot e^{\beta e_\gamma }. \end{align*}
6. High-temperature algorithms
The polymer model we use in the high-temperature region is the same as the one considered in [Reference Borgs, Chayes, Helmuth, Perkins and Tetali2, 8, Reference Helmuth, Jenssen and Perkins21], which we now define. Given a graph
![]() $G=(V,E)$
, the set
$G=(V,E)$
, the set
![]() $\mathcal{P}$
of polymers is the set of connected subgraphs (not necessarily induced) of
$\mathcal{P}$
of polymers is the set of connected subgraphs (not necessarily induced) of
![]() $G$
on at least two vertices. The polymer weights are given by
$G$
on at least two vertices. The polymer weights are given by
![]() $w_\gamma = q^{1 - v_{\gamma }}p^{e_{\gamma }}$
, where we write
$w_\gamma = q^{1 - v_{\gamma }}p^{e_{\gamma }}$
, where we write
![]() $p=e^\beta -1$
. Two polymers
$p=e^\beta -1$
. Two polymers
![]() $\gamma$
and
$\gamma$
and
![]() $\gamma^{\prime}$
are incompatible if and only if their union is connected in
$\gamma^{\prime}$
are incompatible if and only if their union is connected in
![]() $G$
.
$G$
.
The key observation is that edge subsets
![]() $A\subset E$
are in bijection with the collection
$A\subset E$
are in bijection with the collection
![]() $\Omega$
of sets of pairwise compatible polymers by the map taking
$\Omega$
of sets of pairwise compatible polymers by the map taking
![]() $A$
to the set of components of
$A$
to the set of components of
![]() $(V,A)$
on at least two vertices. In this setup, the polymer model partition function
$(V,A)$
on at least two vertices. In this setup, the polymer model partition function
![]() $\Xi$
is given by
$\Xi$
is given by
 \begin{align*} \Xi &= \sum _{\Lambda \in \Omega }\prod _{\gamma \in \Lambda }w_\gamma \\[5pt] &= \sum _{A\subset E}\;\prod _{\substack{\text{components }\gamma \\ \text{of } (V,A)}}\;q^{1-v_\gamma }p^{e_\gamma } \\[5pt] &=\sum _{A\subset E}q^{c(A)-n}(e^\beta -1)^{|A|} = q^{-n} Z_G(q,\beta ), \end{align*}
\begin{align*} \Xi &= \sum _{\Lambda \in \Omega }\prod _{\gamma \in \Lambda }w_\gamma \\[5pt] &= \sum _{A\subset E}\;\prod _{\substack{\text{components }\gamma \\ \text{of } (V,A)}}\;q^{1-v_\gamma }p^{e_\gamma } \\[5pt] &=\sum _{A\subset E}q^{c(A)-n}(e^\beta -1)^{|A|} = q^{-n} Z_G(q,\beta ), \end{align*}
where
![]() $c(A)$
is the number of components of the graph
$c(A)$
is the number of components of the graph
![]() $(V,A)$
. This shows that
$(V,A)$
. This shows that
![]() $q^n \Xi$
is precisely the function which we wish to approximate, and hence any multiplicative approximation to
$q^n \Xi$
is precisely the function which we wish to approximate, and hence any multiplicative approximation to
![]() $\Xi$
corresponds to a multiplicative approximation to
$\Xi$
corresponds to a multiplicative approximation to
![]() $Z$
with the same relative error. Given the standard approach to approximating polymer model partition functions outlined in Section 2.2, to complete our high-temperature algorithm it suffices to verify the conditions of Theorem 6 which imply that the cluster expansion of this polymer model is convergent.
$Z$
with the same relative error. Given the standard approach to approximating polymer model partition functions outlined in Section 2.2, to complete our high-temperature algorithm it suffices to verify the conditions of Theorem 6 which imply that the cluster expansion of this polymer model is convergent.
Lemma 24.
For every
![]() $\epsilon \in (0,1)$
there exist
$\epsilon \in (0,1)$
there exist
![]() $d_0(\epsilon )$
and
$d_0(\epsilon )$
and
![]() $q_0(\epsilon )$
such that for every
$q_0(\epsilon )$
such that for every
![]() $d\ge d_0$
,
$d\ge d_0$
,
![]() $q\ge q_0$
and
$q\ge q_0$
and
![]() $\beta \le (1-\epsilon )\beta _o(q,d)$
, the Kotecký–Preiss condition (see (5) in Theorem 6
) holds for the high-temperature polymer model with
$\beta \le (1-\epsilon )\beta _o(q,d)$
, the Kotecký–Preiss condition (see (5) in Theorem 6
) holds for the high-temperature polymer model with
![]() $f(\gamma )=g(\gamma )=v_\gamma$
.
$f(\gamma )=g(\gamma )=v_\gamma$
.
Proof. We assume that
![]() $d_0(\epsilon )$
and
$d_0(\epsilon )$
and
![]() $q_0(\epsilon )$
are large enough that
$q_0(\epsilon )$
are large enough that
![]() $\beta \leq (1 - \epsilon )\beta _o$
implies that
$\beta \leq (1 - \epsilon )\beta _o$
implies that
![]() $\beta \leq (2-\epsilon )\ln (q)/d$
and hence
$\beta \leq (2-\epsilon )\ln (q)/d$
and hence
![]() $q\ge (1+p)^{d/(2-\epsilon )}$
.
$q\ge (1+p)^{d/(2-\epsilon )}$
.
Write
![]() $\mathcal{P}_{u,k,t}$
for the subset of polymers
$\mathcal{P}_{u,k,t}$
for the subset of polymers
![]() $\gamma \in \mathcal{P}$
such that
$\gamma \in \mathcal{P}$
such that
![]() $\gamma$
contains a fixed vertex
$\gamma$
contains a fixed vertex
![]() $u$
,
$u$
,
![]() $v_\gamma =k$
, and
$v_\gamma =k$
, and
![]() $e_\gamma =t$
. Given an arbitrary polymer
$e_\gamma =t$
. Given an arbitrary polymer
![]() $\gamma$
, we bound from above the sum in the left-hand side of (5) as follows
$\gamma$
, we bound from above the sum in the left-hand side of (5) as follows
Given this and our choice
![]() $f(\gamma ) = v_\gamma$
, it suffices to show that for every vertex
$f(\gamma ) = v_\gamma$
, it suffices to show that for every vertex
![]() $u$
in
$u$
in
![]() $G$
,
$G$
,
Observe that
For
![]() $t \lt k-1$
we have
$t \lt k-1$
we have
![]() $|\mathcal{P}_{u,k,t}|=0$
since polymers must be connected, hence the above sums over
$|\mathcal{P}_{u,k,t}|=0$
since polymers must be connected, hence the above sums over
![]() $t$
start at
$t$
start at
![]() $k-1$
. We bound
$k-1$
. We bound
![]() $|\mathcal{P}_{u,k,t}|$
from above to continue, noting that
$|\mathcal{P}_{u,k,t}|$
from above to continue, noting that
 \begin{equation*} |\mathcal {P}_{u,k,t}| \le \min \left \{ (ed)^{k-1} \cdot \binom {\binom {k}{2} - k + 1}{t - k + 1},\; (ed)^{k-1} \cdot \binom {dk/2 -k + 1}{t - k + 1}\right \}. \end{equation*}
\begin{equation*} |\mathcal {P}_{u,k,t}| \le \min \left \{ (ed)^{k-1} \cdot \binom {\binom {k}{2} - k + 1}{t - k + 1},\; (ed)^{k-1} \cdot \binom {dk/2 -k + 1}{t - k + 1}\right \}. \end{equation*}
To see this, observe that there are at most
![]() $(ed)^{k-1}$
choices of a spanning tree of
$(ed)^{k-1}$
choices of a spanning tree of
![]() $\gamma \in \mathcal{P}_{u,k,t}$
by Proposition 14, and the binomial coefficient gives an upper bound on the number of ways of adding edges of
$\gamma \in \mathcal{P}_{u,k,t}$
by Proposition 14, and the binomial coefficient gives an upper bound on the number of ways of adding edges of
![]() $G$
to this spanning tree to form
$G$
to this spanning tree to form
![]() $\gamma$
. In the case
$\gamma$
. In the case
![]() $k \le d+1$
, we can use
$k \le d+1$
, we can use
![]() $\binom{k}{2}$
as an upper bound on the number of edges of
$\binom{k}{2}$
as an upper bound on the number of edges of
![]() $G$
incident to a vertex of this spanning tree; else, we use
$G$
incident to a vertex of this spanning tree; else, we use
![]() $dk/2$
. Then
$dk/2$
. Then
 \begin{align*} F_u &\le \frac{q}{ed}\sum _{k=2}^{d} (e^3d/q)^k p^{k-1} \sum _{t=k-1}^{\binom{k}{2}} p^{t-k+1}\binom{\binom{k}{2}-k+1}{t-k+1} \\[5pt] & \hphantom{\le{}} + \frac{q}{ed}\sum _{k=d+1}^{\infty } (e^3d/q)^k p^{k-1} \sum _{t=k-1}^{dk/2} p^{t-k+1}\binom{dk/2-k+1}{t-k+1}. \end{align*}
\begin{align*} F_u &\le \frac{q}{ed}\sum _{k=2}^{d} (e^3d/q)^k p^{k-1} \sum _{t=k-1}^{\binom{k}{2}} p^{t-k+1}\binom{\binom{k}{2}-k+1}{t-k+1} \\[5pt] & \hphantom{\le{}} + \frac{q}{ed}\sum _{k=d+1}^{\infty } (e^3d/q)^k p^{k-1} \sum _{t=k-1}^{dk/2} p^{t-k+1}\binom{dk/2-k+1}{t-k+1}. \end{align*}
The inner sums over
![]() $t$
are precisely
$t$
are precisely
![]() $(1+p)^{\binom{k}{2}-k+1}$
and
$(1+p)^{\binom{k}{2}-k+1}$
and
![]() $(1+p)^{dk/2-k+1}$
respectively, so that
$(1+p)^{dk/2-k+1}$
respectively, so that
 \begin{align*} F_u &\le \frac{1+p}{p}\frac{q}{ed}\left (\sum _{k=2}^{d} (e^3dp/q)^k (1+p)^{\binom{k}{2}-k}+ \sum _{k=d+1}^{\infty } (e^3dp/q)^k(1+p)^{dk/2-k}\right ). \end{align*}
\begin{align*} F_u &\le \frac{1+p}{p}\frac{q}{ed}\left (\sum _{k=2}^{d} (e^3dp/q)^k (1+p)^{\binom{k}{2}-k}+ \sum _{k=d+1}^{\infty } (e^3dp/q)^k(1+p)^{dk/2-k}\right ). \end{align*}
Let
![]() $r = e^3 d p(1+p)^{d/2-1}/q$
, and observe that for
$r = e^3 d p(1+p)^{d/2-1}/q$
, and observe that for
![]() $k\in [2,d]$
we have
$k\in [2,d]$
we have
![]() $\binom{k}{2}-k \le \frac{dk}{2}-k-\frac{d}{2}$
. Then
$\binom{k}{2}-k \le \frac{dk}{2}-k-\frac{d}{2}$
. Then
 \begin{align*} F_u &\le \frac{1+p}{p}\frac{q}{ed}\left (\sum _{k=2}^{d} \frac{r^k}{(1+p)^{d/2}}+ \sum _{k=d+1}^{\infty } r^k\right ) = \frac{e^2}{1-r}\left (r-r^d +(1+p)^{d/2}r^d\right ). \end{align*}
\begin{align*} F_u &\le \frac{1+p}{p}\frac{q}{ed}\left (\sum _{k=2}^{d} \frac{r^k}{(1+p)^{d/2}}+ \sum _{k=d+1}^{\infty } r^k\right ) = \frac{e^2}{1-r}\left (r-r^d +(1+p)^{d/2}r^d\right ). \end{align*}
To finish the proof, observe that in order to show
![]() $F_u\le 1$
it suffices to show that
$F_u\le 1$
it suffices to show that
![]() $(1+p)^{1/2}r \le 1/100$
.
$(1+p)^{1/2}r \le 1/100$
.
Substituting the definition of
![]() $r$
and
$r$
and
![]() $q\ge (1+p)^{d/(2-\epsilon )}$
into
$q\ge (1+p)^{d/(2-\epsilon )}$
into
![]() $(1+p)^{1/2}r$
we have
$(1+p)^{1/2}r$
we have
This has a unique stationary point on
![]() $p\in [0,\infty )$
at
$p\in [0,\infty )$
at
![]() $p^*=\frac{4-2 \epsilon }{(d +1)\epsilon -2}$
provided that
$p^*=\frac{4-2 \epsilon }{(d +1)\epsilon -2}$
provided that
![]() $d \ge 10/\epsilon$
(which also ensures that
$d \ge 10/\epsilon$
(which also ensures that
![]() $p^*\gt 0$
), and this stationary point is a maximum. Assuming that
$p^*\gt 0$
), and this stationary point is a maximum. Assuming that
![]() $d\ge 10/\epsilon$
, one can verify that
$d\ge 10/\epsilon$
, one can verify that
![]() $(1+p)^{1/2}r\lt 1/100$
whenever
$(1+p)^{1/2}r\lt 1/100$
whenever
![]() $p \geq 100p^*/\epsilon ^2$
. In terms of
$p \geq 100p^*/\epsilon ^2$
. In terms of
![]() $q$
, to ensure that
$q$
, to ensure that
![]() $p\ge 100p^*/\epsilon ^2$
, it suffices to take
$p\ge 100p^*/\epsilon ^2$
, it suffices to take
![]() $q \gt \exp (400/\epsilon ^3)$
. This establishes Lemma 24.
$q \gt \exp (400/\epsilon ^3)$
. This establishes Lemma 24.
We briefly note that the above proof requires
![]() $\epsilon \gt 0$
so we cannot, for instance, simply allow
$\epsilon \gt 0$
so we cannot, for instance, simply allow
![]() $\epsilon \lt 0$
in order to extend Theorem 1 to all temperatures. However, we can extend our results if we modify our high-temperature polymer model to consider only a subset of polymers – namely, those at most a certain size. We discuss this approach in slightly more detail in Section 9.
$\epsilon \lt 0$
in order to extend Theorem 1 to all temperatures. However, we can extend our results if we modify our high-temperature polymer model to consider only a subset of polymers – namely, those at most a certain size. We discuss this approach in slightly more detail in Section 9.
We also note that Theorem 2 follows from Lemma 24 and the standard method sketched in Subsection 2.2 which uses Theorem 7.
Proof of Theorem
2. As both
![]() $q$
and
$q$
and
![]() $d$
tend to infinity, there exists
$d$
tend to infinity, there exists
![]() $\beta _u(q,d)\sim \ln (q)/d$
such that the Gibbs uniqueness region of the infinite
$\beta _u(q,d)\sim \ln (q)/d$
such that the Gibbs uniqueness region of the infinite
![]() $d$
-regular tree corresponds to
$d$
-regular tree corresponds to
![]() $\beta \lt \beta _u$
(see [Reference Häggström20, Reference Bordewich, Greenhill and Patel6]). Since
$\beta \lt \beta _u$
(see [Reference Häggström20, Reference Bordewich, Greenhill and Patel6]). Since
![]() $\beta _o\sim 2\ln (q)/d$
we can pick (say)
$\beta _o\sim 2\ln (q)/d$
we can pick (say)
![]() $\epsilon =1/4$
in Lemma 24 and so long as
$\epsilon =1/4$
in Lemma 24 and so long as
![]() $d$
and
$d$
and
![]() $q$
are large enough (i.e. at least some absolute constants) we will have the conditions of that lemma, as well as
$q$
are large enough (i.e. at least some absolute constants) we will have the conditions of that lemma, as well as
![]() $\beta _u \le (1-\epsilon )\beta _o$
. The algorithm is given in Subsection 2.2.
$\beta _u \le (1-\epsilon )\beta _o$
. The algorithm is given in Subsection 2.2.
7. Typical structure of the Potts model
In this section, we give a proof of Theorem 4. A useful perspective on the random cluster model comes from tilted bond percolation, providing a distribution on edge subsets of a graph that with
![]() $q=1$
is precisely the usual notion of (independent) bond percolation. For integer
$q=1$
is precisely the usual notion of (independent) bond percolation. For integer
![]() $q$
, there is a coupling between the distributions given by the Potts and random cluster models due to Edwards and Sokal [Reference Edwards and Sokal12] which we now describe. Given a subset of edges from the random cluster model, colour each component with a colour uniformly from
$q$
, there is a coupling between the distributions given by the Potts and random cluster models due to Edwards and Sokal [Reference Edwards and Sokal12] which we now describe. Given a subset of edges from the random cluster model, colour each component with a colour uniformly from
![]() $[q]$
to obtain a vertex colouring distributed according to the Potts model. In reverse, one performs bond percolation (with a particular probability) on the monochromatic components of a colouring from the Potts model. See e.g. [Reference Sokal38] for a thorough treatment of the function
$[q]$
to obtain a vertex colouring distributed according to the Potts model. In reverse, one performs bond percolation (with a particular probability) on the monochromatic components of a colouring from the Potts model. See e.g. [Reference Sokal38] for a thorough treatment of the function
![]() $Z$
and the various combinatorial quantities that it encodes, including the equivalence of (1) and (4).
$Z$
and the various combinatorial quantities that it encodes, including the equivalence of (1) and (4).
Proof of Theorem
4. For part 1, we use the Kotecký–Preiss theorem for the high-temperature cluster expansion to argue that all polymers have size
![]() $O(\ln n)$
with high probability. In order to do this, let
$O(\ln n)$
with high probability. In order to do this, let
![]() $L=(1+\delta )\ln n$
and consider the truncated cluster expansion for
$L=(1+\delta )\ln n$
and consider the truncated cluster expansion for
![]() $\Xi$
. Recall that
$\Xi$
. Recall that
 \begin{equation*} \Xi (L) = \exp \left (\sum _{\substack {\Gamma \in \mathcal {C}\\ g(\Gamma ) \leq L}}\phi (\Gamma )\prod _{\gamma \in \Gamma }w_{\gamma }\right ). \end{equation*}
\begin{equation*} \Xi (L) = \exp \left (\sum _{\substack {\Gamma \in \mathcal {C}\\ g(\Gamma ) \leq L}}\phi (\Gamma )\prod _{\gamma \in \Gamma }w_{\gamma }\right ). \end{equation*}
We have that
![]() $\left |\ln \Xi (L)-\ln \Xi \right |\leq n^{-\delta }$
. Therefore, if we let
$\left |\ln \Xi (L)-\ln \Xi \right |\leq n^{-\delta }$
. Therefore, if we let
![]() $\tilde{Z}_G$
be the sum over configurations with components of size at most
$\tilde{Z}_G$
be the sum over configurations with components of size at most
![]() $L$
, we have
$L$
, we have
and so, with high probability all components are on at most
![]() $(1+\delta )\ln n$
vertices. To get a configuration of the Potts model we make use of the Edwards–Sokal coupling [Reference Edwards and Sokal12] by colouring each component at random with one of the
$(1+\delta )\ln n$
vertices. To get a configuration of the Potts model we make use of the Edwards–Sokal coupling [Reference Edwards and Sokal12] by colouring each component at random with one of the
![]() $q$
colours. Note that if
$q$
colours. Note that if
![]() $C_1,\dots,C_K$
are the components we have
$C_1,\dots,C_K$
are the components we have
 \begin{equation*} \sum _{i=1}^K |C_i|^2 \leq \max _{i \in \{1,\ldots,K\}}|C_i| \cdot \sum _{i = 1}^K|C_i| \leq (1+\delta )n \ln n. \end{equation*}
\begin{equation*} \sum _{i=1}^K |C_i|^2 \leq \max _{i \in \{1,\ldots,K\}}|C_i| \cdot \sum _{i = 1}^K|C_i| \leq (1+\delta )n \ln n. \end{equation*}
Let
![]() $N_j$
be the number of vertices with colour
$N_j$
be the number of vertices with colour
![]() $j$
. Clearly,
$j$
. Clearly,
![]() $\mathbb{E}N_j = n/q$
. By Hoeffding’s inequality ([Reference Hoeffding22], Theorem
$\mathbb{E}N_j = n/q$
. By Hoeffding’s inequality ([Reference Hoeffding22], Theorem
![]() $2$
), we have that
$2$
), we have that
 \begin{equation*} \mathbb {P}\left (\left |N_j - \frac {n}{q}\right | \gt tn \right ) \leq 2 \exp \left (\frac {-2t^2 n^2}{\sum _{i=1}^K |C_i|^2}\right ) \leq 2\exp \left (- \frac {2t^2 n}{(1+\delta )\ln n}\right ). \end{equation*}
\begin{equation*} \mathbb {P}\left (\left |N_j - \frac {n}{q}\right | \gt tn \right ) \leq 2 \exp \left (\frac {-2t^2 n^2}{\sum _{i=1}^K |C_i|^2}\right ) \leq 2\exp \left (- \frac {2t^2 n}{(1+\delta )\ln n}\right ). \end{equation*}
Taking
![]() $t=o\left (\frac{1}{q}\right )\cap \omega \left (\sqrt{\frac{\ln n \cdot \ln q}{n}}\right )$
and a union bound over all colours
$t=o\left (\frac{1}{q}\right )\cap \omega \left (\sqrt{\frac{\ln n \cdot \ln q}{n}}\right )$
and a union bound over all colours
![]() $q$
, we have that with high probability all the
$q$
, we have that with high probability all the
![]() $N_j$
satisfy
$N_j$
satisfy
![]() $N_j=(1+o(1))n/q$
.
$N_j=(1+o(1))n/q$
.
The strengthening of Part 2 now follows. Replacing
![]() $n/2$
with
$n/2$
with
![]() $\delta n$
in (14), we have that
$\delta n$
in (14), we have that
 \begin{align*} \mathbb{P}(\|\boldsymbol{\Lambda }\| \geq (1-\delta )n) &= \mathbb{P}(e^{\|\boldsymbol{\Lambda }\|/d} \ge e^{(1-\delta )n/d})\\[5pt] &\leq \exp \left (\frac{\epsilon n \ln q}{4q^{\epsilon/4}d} - (1-\delta )\frac{n}{d}\right ) \end{align*}
\begin{align*} \mathbb{P}(\|\boldsymbol{\Lambda }\| \geq (1-\delta )n) &= \mathbb{P}(e^{\|\boldsymbol{\Lambda }\|/d} \ge e^{(1-\delta )n/d})\\[5pt] &\leq \exp \left (\frac{\epsilon n \ln q}{4q^{\epsilon/4}d} - (1-\delta )\frac{n}{d}\right ) \end{align*}
This gives us that for some
![]() $\delta = O\left (\frac{\epsilon \ln q}{q^{\epsilon/4}}\right )$
we have
$\delta = O\left (\frac{\epsilon \ln q}{q^{\epsilon/4}}\right )$
we have
Note that there is some subtlety in the final argument. We did not start out by defining the ‘majority colorings’ (those not in
![]() $S_0$
) to be the ones with at least
$S_0$
) to be the ones with at least
![]() $(1-o(1))n$
vertices of the same colour; if we had, the combinatorial arguments necessary to prove the Kotećky-Preiss condition would have been far more difficult (or in some cases false) due to the weakness of our expansion assumptions. Instead, we take a two-layered approach. In the first layer, we use combinatorial arguments to show that
$(1-o(1))n$
vertices of the same colour; if we had, the combinatorial arguments necessary to prove the Kotećky-Preiss condition would have been far more difficult (or in some cases false) due to the weakness of our expansion assumptions. Instead, we take a two-layered approach. In the first layer, we use combinatorial arguments to show that
![]() $Z_G(q,\beta )$
is exponentially well-approximated by the majority colourings, where ‘majority’ here means at least
$Z_G(q,\beta )$
is exponentially well-approximated by the majority colourings, where ‘majority’ here means at least
![]() $\frac{n}2$
vertices of the same colour (Lemma 8). In the second layer, we show that this approximation is itself well-approximated by a polymer model with convergent cluster expansion (Lemma 9). Due to the convergence (Lemma 10), we can discern an even finer level of detail within the polymer model – that the polymer model partition function is itself well-approximated by majority colourings, where we now take ‘majority’ to mean at least
$\frac{n}2$
vertices of the same colour (Lemma 8). In the second layer, we show that this approximation is itself well-approximated by a polymer model with convergent cluster expansion (Lemma 9). Due to the convergence (Lemma 10), we can discern an even finer level of detail within the polymer model – that the polymer model partition function is itself well-approximated by majority colourings, where we now take ‘majority’ to mean at least
![]() $(1-o(1))n$
vertices of the same colour. Our approximations at each step are good enough that we can chain them together to achieve an approximation of our original
$(1-o(1))n$
vertices of the same colour. Our approximations at each step are good enough that we can chain them together to achieve an approximation of our original
![]() $Z_G(q,\beta )$
.
$Z_G(q,\beta )$
.
8. The random cluster model on the discrete hypercube
In this section, we prove Theorem 5 about the existence of a structural phase transition for the random cluster model on the discrete hypercube.
Proof of Theorem
5. The proof of part 1 follows from the proof of part 1 of Theorem 4, which shows that with high probability, each component in the random cluster model has size at most
![]() $(1 + o(1))\ln n \leq \ln _2 n \leq d$
.
$(1 + o(1))\ln n \leq \ln _2 n \leq d$
.
For part 2, suppose there are
![]() $K$
components with vertex sets
$K$
components with vertex sets
![]() $C_1,\dots,C_K$
, where
$C_1,\dots,C_K$
, where
![]() $|C_1| \geq \cdots \geq |C_K|$
. We make use of the Edwards–Sokal coupling [Reference Edwards and Sokal12]. For a subset of edges distributed according to the random cluster model, colour each component at random with one of the
$|C_1| \geq \cdots \geq |C_K|$
. We make use of the Edwards–Sokal coupling [Reference Edwards and Sokal12]. For a subset of edges distributed according to the random cluster model, colour each component at random with one of the
![]() $q$
colours to get a configuration of the Potts model.
$q$
colours to get a configuration of the Potts model.
By (22), every component with more than
![]() $\delta n$
vertices should get the same colour. If there are at least two such components, then the probability of this occurring is at most
$\delta n$
vertices should get the same colour. If there are at least two such components, then the probability of this occurring is at most
![]() $1/q \ll 1$
, thus contradicting (22).
$1/q \ll 1$
, thus contradicting (22).
Henceforth, let us assume that there is at most one component of size at least
![]() $\delta n$
, that is,
$\delta n$
, that is,
![]() $ \max _{i \in \{2,\ldots,K\}}|C_i| \leq \delta n$
. Let
$ \max _{i \in \{2,\ldots,K\}}|C_i| \leq \delta n$
. Let
![]() $n_1 \,{:\!=}\, n - |C_1|$
. We have
$n_1 \,{:\!=}\, n - |C_1|$
. We have
 \begin{equation*} \sum _{i=2}^K |C_i|^2 \leq \max _{i \in \{2,\ldots,K\}}|C_i| \cdot \sum _{i = 2}^K|C_i| = \delta n\cdot n_1. \end{equation*}
\begin{equation*} \sum _{i=2}^K |C_i|^2 \leq \max _{i \in \{2,\ldots,K\}}|C_i| \cdot \sum _{i = 2}^K|C_i| = \delta n\cdot n_1. \end{equation*}
Let
![]() $N_j$
be the number of vertices in components
$N_j$
be the number of vertices in components
![]() $C_2,\ldots C_K$
with colour
$C_2,\ldots C_K$
with colour
![]() $j$
. Clearly,
$j$
. Clearly,
![]() $\mathbb{E}N_j = \frac{n_1}{q}$
. Set
$\mathbb{E}N_j = \frac{n_1}{q}$
. Set
![]() $t = \sqrt{\delta } \cdot \ln q$
. By Hoeffding’s inequality, we have that
$t = \sqrt{\delta } \cdot \ln q$
. By Hoeffding’s inequality, we have that
 \begin{equation*} \mathbb {P}\left (N_j - \frac {n_1}{q} \gt t n_1\right ) \leq \exp \left (\frac {-2t^2 n_1^2}{\sum _{i=2}^K |C_i|^2}\right ) \leq \exp \left (- \frac {2t^2 n_1}{\delta n}\right ). \end{equation*}
\begin{equation*} \mathbb {P}\left (N_j - \frac {n_1}{q} \gt t n_1\right ) \leq \exp \left (\frac {-2t^2 n_1^2}{\sum _{i=2}^K |C_i|^2}\right ) \leq \exp \left (- \frac {2t^2 n_1}{\delta n}\right ). \end{equation*}
If
![]() $n_1 \leq n/\ln q$
, then
$n_1 \leq n/\ln q$
, then
![]() $|C_1| \geq n\left (1 - 1/\ln q\right )$
and we are done. Else, we have that
$|C_1| \geq n\left (1 - 1/\ln q\right )$
and we are done. Else, we have that
![]() $\frac{2t^2 n_1}{\delta n} \geq 2\ln q$
, and so
$\frac{2t^2 n_1}{\delta n} \geq 2\ln q$
, and so
![]() $\mathbb{P}\left (N_j \gt (t+1/q) n_1\right ) \leq e^{-2\ln q} = 1/q^2$
. By taking a union bound over all colours
$\mathbb{P}\left (N_j \gt (t+1/q) n_1\right ) \leq e^{-2\ln q} = 1/q^2$
. By taking a union bound over all colours
![]() $q$
, we have that with high probability all of the
$q$
, we have that with high probability all of the
![]() $N_j$
are smaller than
$N_j$
are smaller than
![]() $(t+1/q) n_1$
, and so with high probability, the largest colour class has at most
$(t+1/q) n_1$
, and so with high probability, the largest colour class has at most
vertices, contradicting (22).
9. Conclusion
We conclude with a discussion on future directions and potential extensions of our arguments.
9.1 Extension to all temperatures
A deceptively simple-sounding task would be to extend our algorithms to work at all temperatures, meaning the range
![]() $(1-\epsilon )\beta _0 \leq \beta \leq (1+\epsilon )\beta _0$
. This requires convergence of both our low- and high-temperature cluster expansions beyond the threshold
$(1-\epsilon )\beta _0 \leq \beta \leq (1+\epsilon )\beta _0$
. This requires convergence of both our low- and high-temperature cluster expansions beyond the threshold
![]() $\beta _0$
. The main results of [Reference Helmuth, Jenssen and Perkins21] show that this must be possible for large enough
$\beta _0$
. The main results of [Reference Helmuth, Jenssen and Perkins21] show that this must be possible for large enough
![]() $q$
and strong enough expansion conditions, so the main interest here is to close the gap without significantly strengthening our assumptions.
$q$
and strong enough expansion conditions, so the main interest here is to close the gap without significantly strengthening our assumptions.
For the high-temperature regime, we can take the same polymer model restricted to polymers on at most
![]() $\frac{n}{2}$
vertices and repeat the argument from Section 6. Subject to the condition of
$\frac{n}{2}$
vertices and repeat the argument from Section 6. Subject to the condition of
![]() $\eta$
-expansion, the constraint in the polymer size allows for better bounds on the size of
$\eta$
-expansion, the constraint in the polymer size allows for better bounds on the size of
![]() $\mathcal P_{u,k,t}$
(the
$\mathcal P_{u,k,t}$
(the
![]() $k$
-vertex
$k$
-vertex
![]() $t$
-edge polymers contained a fixed vertex
$t$
-edge polymers contained a fixed vertex
![]() $u$
), and ultimately lets us establish the Kotecký–Preiss condition for this ’smaller’ polymer model at temperatures slightly beyond
$u$
), and ultimately lets us establish the Kotecký–Preiss condition for this ’smaller’ polymer model at temperatures slightly beyond
![]() $\beta _o$
. There is a delicate interaction between the expansion and improved range of
$\beta _o$
. There is a delicate interaction between the expansion and improved range of
![]() $\beta$
, however, and one must handle the colourings that are no longer represented due to the restriction on polymer size.
$\beta$
, however, and one must handle the colourings that are no longer represented due to the restriction on polymer size.
More significant obstacles appear in extending our low-temperature results. In this regime, our current methods do not extend in a straightforward way beyond
![]() $\beta _0$
unless we allow
$\beta _0$
unless we allow
![]() $q$
to be exponential in
$q$
to be exponential in
![]() $d$
, thus losing some novelty in our results. That is, some extension of what we prove here is plausible, but our conditions seem to degrade and become comparable to the setup of [Reference Helmuth, Jenssen and Perkins21], while still requiring
$d$
, thus losing some novelty in our results. That is, some extension of what we prove here is plausible, but our conditions seem to degrade and become comparable to the setup of [Reference Helmuth, Jenssen and Perkins21], while still requiring
![]() $q$
to be an integer. One possible approach to maintaining
$q$
to be an integer. One possible approach to maintaining
![]() $q$
polynomial in
$q$
polynomial in
![]() $d$
is to improve Lemmas 11 and 12 by providing a better analysis of the partition functions of
$d$
is to improve Lemmas 11 and 12 by providing a better analysis of the partition functions of
![]() $K_{d+1}$
and
$K_{d+1}$
and
![]() $K_{d,d}$
. Even a simple prerequisite such as more a comprehensive version of Lemma 23 that operates in the entire temperature range, appears not to be known. We leave the pursuit of such bounds to future work.
$K_{d,d}$
. Even a simple prerequisite such as more a comprehensive version of Lemma 23 that operates in the entire temperature range, appears not to be known. We leave the pursuit of such bounds to future work.
9.2 Weaker expansion, fewer colours
A natural further direction is to extend our results to a weaker notion of expansion that only guarantees large edge-boundary for small sets, e.g. for some
![]() $k\ge 2$
we have
$k\ge 2$
we have
Such a condition is related to the gap between eigenvalues
![]() $k$
and
$k$
and
![]() $k+1$
of the graph, and it would be interesting to determine whether techniques from combinatorial optimisation that handle small-set expansion and such higher-order eigenvalue gaps can be used for approximating partition functions. This was initiated in [Reference Carlson, Davies and Kolla7] for the low-temperature polymer model that we study here.
$k+1$
of the graph, and it would be interesting to determine whether techniques from combinatorial optimisation that handle small-set expansion and such higher-order eigenvalue gaps can be used for approximating partition functions. This was initiated in [Reference Carlson, Davies and Kolla7] for the low-temperature polymer model that we study here.
We believe that the lower bounds on
![]() $q$
(and to some extent
$q$
(and to some extent
![]() $d$
) in our results are artefacts of our techniques. Extending our results to the case of all
$d$
) in our results are artefacts of our techniques. Extending our results to the case of all
![]() $d,q\ge 3$
presents an interesting challenge, as raised previously in [Reference Helmuth, Jenssen and Perkins21]. The slow mixing results of [Reference Coja-Oghlan, Galanis, Goldberg, Ravelomanana, Stefankovic and Vigoda10] provide some evidence that this may be possible, at least at low temperatures.
$d,q\ge 3$
presents an interesting challenge, as raised previously in [Reference Helmuth, Jenssen and Perkins21]. The slow mixing results of [Reference Coja-Oghlan, Galanis, Goldberg, Ravelomanana, Stefankovic and Vigoda10] provide some evidence that this may be possible, at least at low temperatures.
9.3 Conjectured extension to the random cluster model
It would also be interesting to remove the restriction that
![]() $q$
is an integer and handle the random cluster model directly. That is, are there aspects of our approach that can be extended to work with the more general polymer models of [Reference Helmuth, Jenssen and Perkins21]?
$q$
is an integer and handle the random cluster model directly. That is, are there aspects of our approach that can be extended to work with the more general polymer models of [Reference Helmuth, Jenssen and Perkins21]?
Our high-temperature algorithm already works in the extra generality of the random cluster model, but some of the tools we rely on for the low-temperature algorithm only apply to the Potts model. We conjecture that the results we rely on in Section 5 hold in the required generality.
Conjecture 25.
For all real
![]() $q\gt 1$
and
$q\gt 1$
and
![]() $\beta \gt 0$
, for any graph
$\beta \gt 0$
, for any graph
![]() $G$
we have
$G$
we have
Conjecture 26.
For all real
![]() $q \gt 1$
and
$q \gt 1$
and
![]() $\beta \gt 0$
, for any triangle-free graph
$\beta \gt 0$
, for any triangle-free graph
![]() $G$
we have
$G$
we have
Extending our low-temperature algorithm to the random cluster model may not require results as strong as these conjectures, and instead one could work with analogues of Corollaries 20 and 22 that offer bounds in terms of the total number of edges and maximum degree parameter. So pursuing such slightly weaker results is also of interest. Note that
![]() $q\ge 1$
is required in these conjectures; they do not hold for
$q\ge 1$
is required in these conjectures; they do not hold for
![]() $q \lt 1$
and at
$q \lt 1$
and at
![]() $q=1$
we have
$q=1$
we have
![]() $Z_G(q,\beta ) = e^{\beta e(G)}$
so in this degenerate case the conjectures are trivial.
$Z_G(q,\beta ) = e^{\beta e(G)}$
so in this degenerate case the conjectures are trivial.
Financial support
NF is supported in part by NSF grant CCF-1934964, AK is supported by NSF CAREER grant 1452923, AP is supported in part by NSF grant CCF-1934915, CY is supported in part by NSF grant CCF-1814409 and NSF grant DMS-1800521. An extended abstract of this work appeared at FOCS 2022.
Acknowledgments
This work was undertaken as part of the Phase Transitions and Algorithms working group in the SAMSI Spring 2021 semester programme on Combinatorial Probability. We thank the semester organisers for bringing us together. We also thank Will Perkins and the anonymous referees for helpful feedback on this paper.