Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T23:24:24.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Unusually large components in near-critical Erdős–Rényi graphs via ballot theorems

Part of: Combinatorial probability Stochastic processes

Published online by Cambridge University Press:  11 February 2022

Umberto De Ambroggio  and
Matthew I. Roberts
Umberto De Ambroggio*
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK
Matthew I. Roberts
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the near-critical Erdős–Rényi random graph G(n, p) and provide a new probabilistic proof of the fact that, when p is of the form 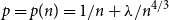$p=p(n)=1/n+\lambda/n^{4/3}$ and A is large,

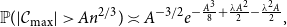\begin{equation*}\mathbb{P}(|\mathcal{C}_{\max}|>An^{2/3})\asymp A^{-3/2}e^{-\frac{A^3}{8}+\frac{\lambda A^2}{2}-\frac{\lambda^2A}{2}},\end{equation*}
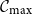where $\mathcal{C}_{\max}$ is the largest connected component of the graph. Our result allows A and 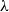$\lambda$ to depend on n. While this result is already known, our proof relies only on conceptual and adaptable tools such as ballot theorems, whereas the existing proof relies on a combinatorial formula specific to Erdős–Rényi graphs, together with analytic estimates.

Keywords

Random graphrandom walkcomponent sizeballot theoremBrownian Motion

MSC classification

Primary: 60C05: Combinatorial probability
Secondary: 60G50: Sums of independent random variables; random walks
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 5 , September 2022 , pp. 840 - 869
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Addario-Berry, L., Broutin, N. and Goldschmidt, C. (2012) The continuum limit of critical random graphs. Probab. Theory Relat. Fields 152(3–4) 367–406.CrossRefGoogle Scholar
Addario-Berry, L. and Reed, B. A. (2008) Ballot theorems, old and new. In Horizons of Combinatorics. Springer, pp. 9–35.Google Scholar
Aldous, D. (1997) Brownian excursions, critical random graphs and the multiplicative coalescent. Ann. Probab. 25(2) 812–854.CrossRefGoogle Scholar
Andreis, L., König, W. and Patterson, R. I. A. (2021) A large-deviations principle for all the cluster sizes of a sparse Erdös-Rényi graph. Random Struct. Alg. 59 522–553.CrossRefGoogle Scholar
Bhamidi, S., van der Hofstad, R. and van Leeuwaarden, J. S. H. (2012) Novel scaling limits for critical inhomogeneous random graphs. Ann. Probab. 40(6) 2299–2361.CrossRefGoogle Scholar
Bhamidi, S., van der Hofstad, R. and van Leeuwaarden, J. S. H. (2010) Scaling limits for critical inhomogeneous random graphs with finite third moments. Electron. J. Probab. 15 1682–1702.CrossRefGoogle Scholar
Bollobás, B. (2001) Random Graphs, 2nd ed., Vol. 73 of Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge.Google Scholar
Bollobás, B. and Riordan, O. (2012) Asymptotic normality of the size of the giant component via a random walk. J. Comb. Theory Ser. B 102(1) 53–61.CrossRefGoogle Scholar
Chatterjee, S. (2012) A new approach to strong embeddings. Probab. Theory Relat. Fields 152(1–2) 231–264.CrossRefGoogle Scholar
De Ambroggio, U. (2021) An elementary approach to component sizes in critical random graphs. Preprint: https://arxiv.org/abs/2101.06625.Google Scholar
De Ambroggio, U. and Pachon, A. (2020) Simple upper bounds for the largest components in critical inhomogeneous random graphs. Preprint: http://arxiv.org/abs/2012.09001.Google Scholar
Dembo, A., Levit, A. and Vadlamani, S. (2019) Component sizes for large quantum Erdös-Rényi graph near criticality. Ann. Probab. 47(2) 1185–1219.CrossRefGoogle Scholar
Dhara, S., van der Hofstad, R., van Leeuwaarden, J. S. H. and Sen, S. (2017) Critical window for the configuration model: finite third moment degrees. Electron. J. Probab. 22(16) 1–33.CrossRefGoogle Scholar
Durrett, R. (1978) Conditioned limit theorems for some null-recurrent Markov processes. Ann. Probab. 6(5) 798–828.CrossRefGoogle Scholar
Janson, S., Luczak, T. and Rucinski, A. (2011) Random Graphs, Vol. 45. John Wiley & Sons, New York.Google Scholar
Joseph, A. (2014) The component sizes of a critical random graph with given degree sequence. Ann. Appl. Probab. 24(6) 2560–2594.CrossRefGoogle Scholar
Kager, W. (2011) The hitting time theorem revisited. Am. Math. Mon. 118(8) 735–737.CrossRefGoogle Scholar
Komlós, J., Major, P. and Tusnády, G. (1975) An approximation of partial sums of independent RV’-s, and the sample DF. I. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete 32(1–2) 111–131.CrossRefGoogle Scholar
Konstantopoulos, T. (1995) Ballot theorems revisited. Stat. Probab. Lett. 24(4) 331–338.CrossRefGoogle Scholar
Łuczak, T., Pittel, B. and Wierman, J. C. (1994) The structure of a random graph at the point of the phase transition. Trans. Am. Math. Soc. 341(2) 721–748.CrossRefGoogle Scholar
Martin-Löf, A. (1986) Symmetric sampling procedures, general epidemic processes and their threshold limit theorems. J. Appl. Probab. 23(2) 265–282.CrossRefGoogle Scholar
Nachmias, A. and Peres, Y. (2007) Component sizes of the random graph outside the scaling window. ALEA Latin Am. J. Probab. Math. Stat. 3 133–142.Google Scholar
Nachmias, A. and Peres, Y. (2010) Critical percolation on random regular graphs. Random Struct. Alg. 36(2) 111–148.CrossRefGoogle Scholar
Nachmias, A. and Peres, Y. (2010) The critical random graph, with martingales. Israel J. Math. 176 29–41.CrossRefGoogle Scholar
O’Connell, N. (1998) Some large deviation results for sparse random graphs. Probab. Theory Related Fields 110(3)277–285.CrossRefGoogle Scholar
Pittel, B. (2001) On the largest component of the random graph at a nearcritical stage. J. Comb. Theory Ser. B 82(2) 237–269.CrossRefGoogle Scholar
Riordan, O. (2012) The phase transition in the configuration model. Comb. Probab. Comput. 21(1–2) 265–299.CrossRefGoogle Scholar
Roberts, M. I. (2017) The probability of unusually large components in the near-critical Erdös-Rényi graph. Adv. Appl. Probab. 50(1) 245–271.CrossRefGoogle Scholar
Rossignol, R. (2021) Scaling limit of dynamical percolation on critical Erdös-Rényi random graphs. Ann. Probab. 49(1) 322–399.CrossRefGoogle Scholar
Spitzer, F. (1960) A Tauberian theorem and its probability interpretation. Trans. Am. Math. Soc. 94(1) 150–179.CrossRefGoogle Scholar
Strassen, V. (1967) Almost sure behavior of sums of independent random variables and martingales. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 2: Contributions to Probability Theory, Part 1. The Regents of the University of California.Google Scholar
van der Hofstad, R. (2016) Random Graphs and Complex Networks, Vol. 1. Cambridge University Press, Cambridge.CrossRefGoogle Scholar
van der Hofstad, R., Janssen, A. J. E. M. and van Leeuwaarden, J. S. H. (2010) Critical epidemics, random graphs, and Brownian motion with a parabolic drift. Adv. Appl. Probab. 42(4) 1187–1206.CrossRefGoogle Scholar
van der Hofstad, R., Kager, W. and Müller, T. (2009) A local limit theorem for the critical random graph. Electron. Commun. Probab. 14 122–131.CrossRefGoogle Scholar
van der Hofstad, R. and Keane, M. (2008) An elementary proof of the hitting time theorem. Am. Math. Mon. 115(8) 753–756.CrossRefGoogle Scholar
van der Hofstad, R., Kliem, S. and van Leeuwaarden, J. S. H. (2018) Cluster tails for critical power-law inhomogeneous random graphs. J. Stat. Phys. 171(1) 38–95.CrossRefGoogle ScholarPubMed