Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T19:45:31.730Z Has data issue: false hasContentIssue false
  • English
  • Français

A Threshold Phenomenon for Random Independent Sets in the Discrete Hypercube

Published online by Cambridge University Press:  02 July 2010

DAVID GALVIN
DAVID GALVIN*
Affiliation:
Department of Mathematics, University of Notre Dame, 255 Hurley Hall, Notre Dame, IN 46556, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let I be an independent set drawn from the discrete d-dimensional hypercube Qd = {0, 1}d according to the hard-core distribution with parameter λ > 0 (that is, the distribution in which each independent set I is chosen with probability proportional to λ|I|). We show a sharp transition around λ = 1 in the appearance of I: for λ > 1, min{|I ∩ Ɛ|, |I ∩ 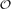|} = 0 asymptotically almost surely, where Ɛ and 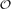are the bipartition classes of Qd, whereas for λ < 1, min{|I ∩ Ɛ|, |I ∩ 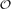|} is asymptotically almost surely exponential in d. The transition occurs in an interval whose length is of order 1/d.

A key step in the proof is an estimation of Zλ(Qd), the sum over independent sets in Qd with each set I given weight λ|I| (a.k.a. the hard-core partition function). We obtain the asymptotics of Zλ(Qd) for 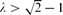, and nearly matching upper and lower bounds for 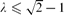, extending work of Korshunov and Sapozhenko. These bounds allow us to read off some very specific information about the structure of an independent set drawn according to the hard-core distribution.

We also derive a long-range influence result. For all fixed λ > 0, if I is chosen from the independent sets of Qd according to the hard-core distribution with parameter λ, conditioned on a particular v ∈ Ɛ being in I, then the probability that another vertex w is in I is o(1) for w ∈ 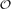but Ω(1) for w ∈ Ɛ.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 20 , Issue 1 , January 2011 , pp. 27 - 51
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bollobás, B. (1998) Modern Graph Theory, Springer, New York.CrossRefGoogle Scholar
[2]Brightwell, G. and Winkler, P. (2002) Hard constraints and the Bethe lattice: Adventures at the interface of combinatorics and statistical physics. In Proc. Int. Congress of Mathematicians Vol. III (Tatsien, Li, ed.), Higher Education Press, Beijing, pp. 605–624.Google Scholar
[3]Galvin, D. (2003) On homomorphisms from the Hamming cube to ℤ. Israel J. Math. 138 189–213.CrossRefGoogle Scholar
[4]Galvin, D. Independent sets of a fixed size in the discrete hypercube. In preparation.Google Scholar
[5]Galvin, D. and Kahn, J. (2004) On phase transition in the hard-core model on ℤd. Combin. Probab. Comput. 13 137–164.Google Scholar
[6]Galvin, D. and Tetali, P. (2006) Slow mixing of the Glauber dynamics for the hard-core model on the Hamming cube. Random Struct. Alg. 28 427–443.CrossRefGoogle Scholar
[7]Hoeffding, W. (1963) Probability inequalities for sums of bounded random variables. J. Amer. Statist. Assoc. 58 13–30.CrossRefGoogle Scholar
[8]Kahn, J. (2001) An entropy approach to the hard-core model on bipartite graphs. Combin. Probab. Comput. 10 219–237.Google Scholar
[9]Korshunov, A. and Sapozhenko, A. (1983) The number of binary codes with distance 2. Problemy Kibernet. 40 111–130. (In Russian.)Google Scholar
[10]Lovász, L. (1975) On the ratio of optimal integral and fractional covers. Discrete Math. 13 383–390.CrossRefGoogle Scholar
[11]Sapozhenko, A. (1987) On the number of connected subsets with given cardinality of the boundary in bipartite graphs. Metody Diskret. Analiz. 45 42–70. (In Russian.)Google Scholar
[12]Sapozhenko, A. (1989) The number of antichains in ranked partially ordered sets. Diskret. Mat. 1 74–93. (In Russian; translation in Discrete Math. Appl. 1 (1991) 35–58.)Google Scholar
[13]Stein, S. K. (1974) Two combinatorial covering theorems. J. Combin. Theory Ser. A 16 391–397.CrossRefGoogle Scholar