Article contents
Strong complete minors in digraphs
Published online by Cambridge University Press: 24 September 2021
Abstract
Kostochka and Thomason independently showed that any graph with average degree 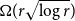 $\Omega(r\sqrt{\log r})$
contains a
$\Omega(r\sqrt{\log r})$
contains a 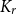 $K_r$
minor. In particular, any graph with chromatic number
$K_r$
minor. In particular, any graph with chromatic number 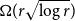 $\Omega(r\sqrt{\log r})$
contains a
$\Omega(r\sqrt{\log r})$
contains a 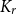 $K_r$
minor, a partial result towards Hadwiger’s famous conjecture. In this paper, we investigate analogues of these results in the directed setting. There are several ways to define a minor in a digraph. One natural way is as follows. A strong
$K_r$
minor, a partial result towards Hadwiger’s famous conjecture. In this paper, we investigate analogues of these results in the directed setting. There are several ways to define a minor in a digraph. One natural way is as follows. A strong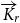 $\overrightarrow{K}_{\!\!r}$
minor is a digraph whose vertex set is partitioned into r parts such that each part induces a strongly connected subdigraph, and there is at least one edge in each direction between any two distinct parts. We investigate bounds on the dichromatic number and minimum out-degree of a digraph that force the existence of strong
$\overrightarrow{K}_{\!\!r}$
minor is a digraph whose vertex set is partitioned into r parts such that each part induces a strongly connected subdigraph, and there is at least one edge in each direction between any two distinct parts. We investigate bounds on the dichromatic number and minimum out-degree of a digraph that force the existence of strong 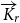 $\overrightarrow{K}_{\!\!r}$
minors as subdigraphs. In particular, we show that any tournament with dichromatic number at least 2r contains a strong
$\overrightarrow{K}_{\!\!r}$
minors as subdigraphs. In particular, we show that any tournament with dichromatic number at least 2r contains a strong 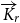 $\overrightarrow{K}_{\!\!r}$
minor, and any tournament with minimum out-degree
$\overrightarrow{K}_{\!\!r}$
minor, and any tournament with minimum out-degree 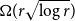 $\Omega(r\sqrt{\log r})$
also contains a strong
$\Omega(r\sqrt{\log r})$
also contains a strong 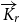 $\overrightarrow{K}_{\!\!r}$
minor. The latter result is tight up to the implied constant and may be viewed as a strong-minor analogue to the classical result of Kostochka and Thomason. Lastly, we show that there is no function
$\overrightarrow{K}_{\!\!r}$
minor. The latter result is tight up to the implied constant and may be viewed as a strong-minor analogue to the classical result of Kostochka and Thomason. Lastly, we show that there is no function 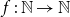 $f\;:\;\mathbb{N} \rightarrow \mathbb{N}$
such that any digraph with minimum out-degree at least f(r) contains a strong
$f\;:\;\mathbb{N} \rightarrow \mathbb{N}$
such that any digraph with minimum out-degree at least f(r) contains a strong 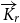 $\overrightarrow{K}_{\!\!r}$
minor, but such a function exists when considering dichromatic number.
$\overrightarrow{K}_{\!\!r}$
minor, but such a function exists when considering dichromatic number.
Keywords
MSC classification
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 2
- Cited by



