Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T01:46:34.790Z Has data issue: false hasContentIssue false
  • English
  • Français

Set Families With a Forbidden Induced Subposet

Published online by Cambridge University Press:  22 March 2012

EDWARD BOEHNLEIN  and
TAO JIANG
EDWARD BOEHNLEIN
Affiliation:
Department of Mathematics, Miami University, Oxford, OH 45056, USA (e-mail: [email protected], [email protected])
TAO JIANG
Affiliation:
Department of Mathematics, Miami University, Oxford, OH 45056, USA (e-mail: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

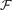For each poset H whose Hasse diagram is a tree of height k, we show that the largest size of a family of subsets of [n]={1,. . ., n} not containing H as an induced subposet is asymptotic to 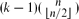. This extends a result of Bukh [1], which in turn generalizes several known results including Sperner's theorem.

Keywords

Primary 06A0705D05
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 4 , July 2012 , pp. 496 - 511
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bukh, B. (2009) Set families with a forbidden subposet. Electron. J. Combin. 16 #R142.CrossRefGoogle Scholar
[2]Carroll, T. and Katona, G. O. H. (2008) Bounds on maximal families of sets not containing three sets with A∪B⊂C, A∉⊂B. Order 25 229–236.CrossRefGoogle Scholar
[3]De Bonis, A. and Katona, G. O. H. (2007) Largest families without an r-fork. Order 24 181–191.CrossRefGoogle Scholar
[4]De Bonis, A., Katona, G. O. H. and Swanepoel, K. J. (2005) Largest families without A∪B⊂C∩D. J. Combin. Theory Ser. A 111 331–336.CrossRefGoogle Scholar
[5]Erdős, P. (1945) On a lemma of Littlewood and Offord. Bull. Amer. Math. Soc. 51 898–902.CrossRefGoogle Scholar
[6]Griggs, J. and Lu, L. (2009) On families of subsets with a forbidden subposet. Combin. Probab. Comput. 18 731–748.CrossRefGoogle Scholar
[7]Sperner, E. (1928) Ein Satz über Untermengen einer endlichen Menge. Math. Z. 27 544–548.CrossRefGoogle Scholar
[8]Thanh, H. T. (1998) An extremal problem with excluded subposets in the Boolean lattice. Order 15 51–57.CrossRefGoogle Scholar