Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T18:50:08.108Z Has data issue: false hasContentIssue false
  • English
  • Français

The Probability That a Random Multigraph is Simple

Published online by Cambridge University Press:  01 March 2009

SVANTE JANSON
SVANTE JANSON*
Affiliation:
Department of Mathematics, Uppsala University, PO Box 480, SE-751 06 Uppsala, Sweden (e-mail: [email protected]://www.math.uu.se/~svante/)
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a random multigraph G* with given vertex degrees d1,. . .,dn, constructed by the configuration model. We show that, asymptotically for a sequence of such multigraphs with the number of edges 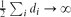, the probability that the multigraph is simple stays away from 0 if and only if 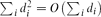. This was previously known only under extra assumptions on the maximum degree maxidi. We also give an asymptotic formula for this probability, extending previous results by several authors.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 18 , Issue 1-2: Papers from The 2006 Oberwolfach Meeting on Combinatorics, Probability and Computing , March 2009 , pp. 205 - 225
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bender, E. A. and Canfield, E. R. (1978) The asymptotic number of labeled graphs with given degree sequences. J. Combin. Theory Ser. A 24 296–307.CrossRefGoogle Scholar
[2]Bollobás, B. (1980) A probabilistic proof of an asymptotic formula for the number of labelled regular graphs. Europ. J. Combin. 1 311–316.CrossRefGoogle Scholar
[3]Bollobás, B. (2001) Random Graphs, 2nd edn, Cambridge University Press, Cambridge.CrossRefGoogle Scholar
[4]Cooper, C. (2004) The cores of random hypergraphs with a given degree sequence. Random Struct. Alg. 25 353–375.CrossRefGoogle Scholar
[5]Cooper, C. and Frieze, A. (2004) The size of the largest strongly connected component of a random digraph with a given degree sequence. Combin. Probab. Comput. 13 319–337.CrossRefGoogle Scholar
[6]Gut, A. (2005) Probability: A Graduate Course, Springer, New York.Google Scholar
[7]Janson, S. and Luczak, M. (2007) A simple solution to the k-core problem. Random Struct. Alg. 30 50–62.CrossRefGoogle Scholar
[8]Janson, S., Luczak, T. and Ruciński, A. (2000) Random Graphs, Wiley, New York.CrossRefGoogle Scholar
[9]McKay, B. D. (1984) Asymptotics for 0–1 matrices with prescribed line sums. In Enumeration and Design (Waterloo, Ont., 1982), Academic Press, Toronto, ON, pp. 225–238.Google Scholar
[10]McKay, B. D. (1985) Asymptotics for symmetric 0–1 matrices with prescribed row sums. Ars Combin. 19A 15–25.Google Scholar
[11]McKay, B. D. and Wormald, N. C. (1990) Uniform generation of random regular graphs of moderate degree. J. Algorithms 11 52–67.CrossRefGoogle Scholar
[12]McKay, B. D. and Wormald, N. C. (1990) Asymptotic enumeration by degree sequence of graphs of high degree. Europ. J. Combin. 11 565–580.CrossRefGoogle Scholar
[13]McKay, B. D. and Wormald, N. C. (1991) Asymptotic enumeration by degree sequence of graphs with degrees o(n 1/2). Combinatorica 11 369–382.CrossRefGoogle Scholar
[14]Wormald, N. C. (1978) Some problems in the enumeration of labelled graphs. PhD thesis, University of Newcastle.Google Scholar
[15]Wormald, N. C. (1981) The asymptotic distribution of short cycles in random regular graphs. J. Combin. Theory Ser. B 31 168–182.CrossRefGoogle Scholar