Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T16:40:34.188Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Richter–Thomassen Conjecture about Pairwise Intersecting Closed Curves†

Part of: Extremal combinatorics Discrete geometry Graph theory

Published online by Cambridge University Press:  04 May 2016

JÁNOS PACH ,
NATAN RUBIN  and
GÁBOR TARDOS
JÁNOS PACH
Affiliation:
École Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland and Alfréd Rényi Institute of Mathematics, Realtanoda utca 13-15, H-1053, Budapest (e-mail: [email protected])
NATAN RUBIN
Affiliation:
Department of Computer Science, Ben-Gurion University of the Negev, Beer-Sheva 84105, Israel (e-mail: [email protected])
GÁBOR TARDOS
Affiliation:
Alfréd Rényi Institute of Mathematics, Realtanoda utca 13-15, H-1053, Budapest (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A long-standing conjecture of Richter and Thomassen states that the total number of intersection points between any n simple closed Jordan curves in the plane, so that any pair of them intersect and no three curves pass through the same point, is at least (1−o(1))n 2.

We confirm the above conjecture in several important cases, including the case (1) when all curves are convex, and (2) when the family of curves can be partitioned into two equal classes such that each curve from the first class touches every curve from the second class. (Two closed or open curves are said to be touching if they have precisely one point in common and at this point the two curves do not properly cross.)

An important ingredient of our proofs is the following statement. Let S be a family of n open curves in ℝ2, so that each curve is the graph of a continuous real function defined on ℝ, and no three of them pass through the same point. If there are nt pairs of touching curves in S, then the number of crossing points is 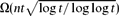$\Omega(nt\sqrt{\log t/\log\log t})$ .

MSC classification

Primary: 52C45: Combinatorial complexity of geometric structures
Secondary: 05C10: Planar graphs; geometric and topological aspects of graph theory 05C35: Extremal problems 05D99: None of the above, but in this section 52C10: Erdős problems and related topics of discrete geometry 52C30: Planar arrangements of lines and pseudolines
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 6 , November 2016 , pp. 941 - 958
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

A preliminary version of this paper appeared in Proc. 26th Annual ACM–SIAM Symposium on Discrete Algorithms (2015), pp. 1506–1516.

References

[1] Agarwal, P. K., Nevo, E., Pach, J., >Pinchasi, R., Sharir, M. and Smorodinsky, S. (2004) Lenses in arrangements of pseudocircles and their applications. J. Assoc. Comput. Mach. 51 139–186.CrossRefGoogle Scholar
[2] Agarwal, P. K. and Sharir, M. (2005) Pseudo-line arrangements: Duality, algorithms, and applications. SIAM J. Comput. 34 526–552.CrossRefGoogle Scholar
[3] Aronov, B. and Sharir, M. (2002) Cutting circles into pseudo-segments and improved bounds for incidences. Discrete Comput. Geom. 28 475–490.CrossRefGoogle Scholar
[4] Brass, P., Moser, W. and Pach, J. (2005) Research Problems in Discrete Geometry, Springer.Google Scholar
[5] Chan, T. M. (2003) On levels in arrangements of curves. Discrete Comput. Geom. 29 375–393. Also in Proc. 41th IEEE Sympos. Found. Comput. Sci.: FOCS (2000), pp. 219–227.CrossRefGoogle Scholar
[6] Chan, T. M. (2005) On levels in arrangements of curves II: A simple inequality and its consequence. Discrete Comput. Geom. 34 11–24. Also in Proc. 44th IEEE Sympos. Found. Comput. Sci.: FOCS (2003), pp. 544–550.CrossRefGoogle Scholar
[7] Chan, T. M. (2008) On levels in arrangements of curves III: Further improvements. In Proc. 24th ACM Symposium on Computational Geometry: SoCG, pp. 85–93.CrossRefGoogle Scholar
[8] Edelsbrunner, H. (1987) Algorithms in Combinatorial Geometry, Vol. 10 of EATCS Monographs on Theoretical Computer Science, Springer.CrossRefGoogle Scholar
[9] Erdős, P. (1946) On sets of distances of n points. Amer. Math. Monthly 53 248–250.CrossRefGoogle Scholar
[10] Fox, J., Frati, F., Pach, J. and Pinchasi, R. (2010) Crossings between curves with many tangencies. In WALCOM: Algorithms and Computation, Vol. 5942 of Lecture Notes in Computer Science, Springer, pp. 1–8. Also in An Irregular Mind, Vol. 21 of Bolyai Society Mathematical Studies (2010), János Bolyai Mathematical Society, pp. 251–260.Google Scholar
[11] Holtzman, J. M. and Halkin, H. (1966) Directional convexity and the maximum principle for discrete systems. SIAM J. Control 4 263–275.CrossRefGoogle Scholar
[12] Kaplan, H., >Matoušek, J. and Sharir, M. (2012) Simple proofs of classical theorems in discrete geometry via the Guth–Katz polynomial partitioning technique. Discrete Comput. Geom. 48 499–517.CrossRefGoogle Scholar
[13] Kedem, K., Livné, R., Pach, J. and Sharir, M. (1986) On the union of Jordan regions and collision-free translational motion amidst polygonal obstacles. Discrete Comput. Geom. 1 59–71.CrossRefGoogle Scholar
[14] Marcus, A. and Tardos, G. (2006) Intersection reverse sequences and geometric applications. J. Combin. Theory Ser. A 113 675–691.CrossRefGoogle Scholar
[15] Mubayi, D. (2002) Intersecting curves in the plane. Graphs Combin. 18 583–589.Google Scholar
[16] Pach, J. and Sharir, M. (2009) Combinatorial Geometry and its Algorithmic Applications: The Alcalá Lectures, Vol. 152 of Mathematical Surveys and Monographs, AMS.Google Scholar
[17] Pach, J., Rubin, N. and Tardos, G. Beyond the Richter–Thomassen conjecture. In Proc. 27th Annual ACM–SIAM Symposium on Discrete Algorithms: SODA 2016, pp. 957–968.CrossRefGoogle Scholar
[18] Richter, R. B. and Thomassen, C. (1995) Intersections of curve systems and the crossing number of C 5 × C 5 . Discrete Comput. Geom. 13 149–159.CrossRefGoogle Scholar
[19] Salazar, G. (1999) On the intersections of systems of curves. J. Combin. Theory Ser. B 75 56–60.CrossRefGoogle Scholar
[20] Sharir, M. and Agarwal, P. K. (1995) Davenport–Schinzel Sequences and Their Geometric Applications, Cambridge University Press.Google Scholar
[21] Solymosi, J. and Tao, T. (2012) An incidence theorem in higher dimensions. Discrete Comput. Geom. 48 255–280.CrossRefGoogle Scholar
[22] Székely, L. A. (1997) Crossing numbers and hard Erdős problems in discrete geometry. Combin. Probab. Comput. 6 353–358.CrossRefGoogle Scholar
[23] Szemerédi, E. and Trotter, W. T. Jr (1983) Extremal problems in discrete geometry. Combinatorica 3 381–392.CrossRefGoogle Scholar
[24] Szemerédi, E. and Trotter, W. T. Jr (1983) A combinatorial distinction between the Euclidean and projective planes. European J. Combin. 4 385–394.CrossRefGoogle Scholar
[25] Tamaki, H. and Tokuyama, T. (1998) How to cut pseudoparabolas into segments. Discrete Comput. Geom. 19 265–290.CrossRefGoogle Scholar
[26] Tao, T. and Vu, V. H. (2010) Additive Combinatorics, Vol. 105 of Cambridge Studies in Advanced Mathematics, Cambridge University Press.Google Scholar