Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T11:01:10.805Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Independence Number of Steiner Systems

Published online by Cambridge University Press:  30 January 2013

ALEX EUSTIS  and
JACQUES VERSTRAËTE
ALEX EUSTIS
Affiliation:
Department of Mathematics, UCSD, 9500 Gilman Drive, La Jolla, CA 92093-0112, USA (e-mail: [email protected])
JACQUES VERSTRAËTE
Affiliation:
Department of Mathematics, UCSD, 9500 Gilman Drive, La Jolla, CA 92093-0112, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

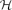A partial Steiner (n,r,l)-system is an r-uniform hypergraph on n vertices in which every set of l vertices is contained in at most one edge. A partial Steiner (n,r,l)-system is complete if every set of l vertices is contained in exactly one edge. In a hypergraph , the independence number α(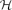) denotes the maximum size of a set of vertices in 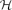containing no edge. In this article we prove the following. Given integers r,l such that r ≥ 2l − 1 ≥ 3, we prove that there exists a partial Steiner (n,r,l)-system 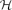such that

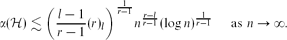$$\alpha(\HH) \lesssim \biggl(\frac{l-1}{r-1}(r)_l\biggr)^{\frac{1}{r-1}}n^{\frac{r-l}{r-1}} (\log n)^{\frac{1}{r-1}} \quad \mbox{ as }n \rightarrow \infty.$$
This improves earlier results of Phelps and Rödl, and Rödl and Ŝinajová. We conjecture that it is best possible as it matches the independence number of a random r-uniform hypergraph of the same density. If l = 2 or l = 3, then for infinitely many r the partial Steiner systems constructed are complete for infinitely many n.

Keywords

Primary 05B05Secondary 05B0705B2005B2505D40
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 2 , March 2013 , pp. 241 - 252
Copyright
Copyright © Cambridge University Press 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ajtai, M., Komlós, J., Pintz, J., Spencer, J. and Szemerédi, E. (1982) Extremal uncrowded hypergraphs. J. Combin. Theory Ser. A 32 321–335.CrossRefGoogle Scholar
[2]Alon, N., Mellinger, K., Mubayi, D. and Verstraëte, J. (2011) The de Bruijn–Erdős theorem for hypergraphs. Submitted.Google Scholar
[3]Alon, N. and Spencer, J. (2000) The Probabilistic Method, second edition, Wiley.Google Scholar
[4]Caro, Y. and Tuza, Z. (1991) Improved lower bounds on $k$-independence. J. Graph Theory 15 99–107.Google Scholar
[5]Colbourn, C. and Dinitz, J., eds (1996) The CRC Handbook of Combinatorial Designs, CRC Press.Google Scholar
[6]Dembowski, P. (1996) Finite Geometries, Springer. Reprint of 1968 edition.Google Scholar
[7]Duke, R., Lefmann, H. and Rödl, V. (1995) On uncrowded hypergraphs. Random Struct. Alg. 6 209–212.CrossRefGoogle Scholar
[8]Eustis, A. and Verstraëte, J. (2012) Independent sets in randomized construction of Steiner (n,r,r-1)-systems. Preprint.Google Scholar
[9]Erdős, P. and Hanani, H. (1963) On a limit theorem in combinatorial analysis. Publ. Math. Debrecen 10 10–13.CrossRefGoogle Scholar
[10]Frieze, A. and Mubayi, D. (2008) On the chromatic number of simple triangle-free triple systems. Electron. J. Combin. 15 R121.Google Scholar
[11]Frieze, A. and Mubayi, D. (2008) Coloring simple hypergraphs. Preprint.Google Scholar
[12]Füredi, Z. (1991) Maximal independent subsets in Steiner systems and in planar sets. SIAM J. Discrete Math. 4 196–199Google Scholar
[13]Haemers, W. (1980) Eigenvalue techniques in design and graph theory. PhD thesis, Technical University Eindhoven. Math. Centre Tract 121, Mathematical Centre, Amsterdam.Google Scholar
[14]Hajnal, A. and Szemerédi, E. (1970) Proof of a conjecture of Erdős. Combin. Theory Appl. 2 601–623.Google Scholar
[15]Keevash, P., Sudakov, B. and Verstraëte, J. (2011) On a conjecture of Erdős and Simonovits: Even Cycles. Combinatorica. (accepted).Google Scholar
[16]Kirkman, T. (1847) On a problem in combinations. The Cambridge and Dublin Mathematical Journal (Macmillan, Barclay, and Macmillan) II 191–204.Google Scholar
[17]Komlós, J., Pintz, J. and Szemerédi, E. (1982) A lower bound for Heilbronn's problem. J. London Math. Soc. (2) 25 13–24.Google Scholar
[18]Kostochka, A., Mubayi, D. and Verstraëte, J. (2011) On independent sets in hypergraphs. Random Struct. Alg. (accepted).Google Scholar
[19]Krivelevich, M. and Sudakov, B. (1998) The chromatic numbers of random hypergraphs. Random Struct. Alg. 12 381–403.Google Scholar
[20]Phelps, K. and Rödl, V. (1986) Steiner triple systems with minimum independence number. Ars Combin. 21 167–172.Google Scholar
[21]Rödl, V. (1985) On a packing and covering problem. Europ. J. Combin. 6 69–78.Google Scholar
[22]Rödl, V. and Ŝinajová, V. (1994) Note on independent sets in Steiner systems. Random Struct. Alg. 5 183–190.Google Scholar
[23]Shearer, J. (1983) A note on the independence number of triangle-free graphs. Discrete Math. 46 83–87.Google Scholar
[24]Wilson, R. (1975) An existence theorem for pairwise balanced designs III: Proof of the existence conjecture. J. Combin. Theory Ser. A 18 71–79.Google Scholar