Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ramamurthi, Radhika
and
West, Douglas B.
2004.
Maximum face-constrained coloring of plane graphs.
Discrete Mathematics,
Vol. 274,
Issue. 1-3,
p.
233.
Axenovich, Maria
Jiang, Tao
and
Kündgen, André
2004.
Bipartite anti‐Ramsey numbers of cycles.
Journal of Graph Theory,
Vol. 47,
Issue. 1,
p.
9.
Schiermeyer, Ingo
2004.
Rainbow numbers for matchings and complete graphs.
Discrete Mathematics,
Vol. 286,
Issue. 1-2,
p.
157.
Jiang, Tao
and
West, Douglas B.
2004.
Edge-colorings of complete graphs that avoid polychromatic trees.
Discrete Mathematics,
Vol. 274,
Issue. 1-3,
p.
137.
Sárközy, Gábor N.
and
Selkow, Stanley
2006.
On an anti‐Ramsey problem of Burr, Erdős, Graham, and T. Sós.
Journal of Graph Theory,
Vol. 52,
Issue. 2,
p.
147.
Gorgol, Izolda
and
Łazuka, Ewa
2006.
Rainbow numbers for certain graphs.
Electronic Notes in Discrete Mathematics,
Vol. 24,
Issue. ,
p.
77.
Jiang, Tao
and
Pikhurko, Oleg
2009.
Anti‐Ramsey numbers of doubly edge‐critical graphs.
Journal of Graph Theory,
Vol. 61,
Issue. 3,
p.
210.
Li, Xueliang
and
Xu, Zhixia
2009.
The rainbow number of matchings in regular bipartite graphs.
Applied Mathematics Letters,
Vol. 22,
Issue. 10,
p.
1525.
Fujita, Shinya
Magnant, Colton
and
Ozeki, Kenta
2010.
Rainbow Generalizations of Ramsey Theory: A Survey.
Graphs and Combinatorics,
Vol. 26,
Issue. 1,
p.
1.
Gorgol, Izolda
2016.
Anti-Ramsey numbers in complete split graphs.
Discrete Mathematics,
Vol. 339,
Issue. 7,
p.
1944.
Jin, Zemin
Nweit, Oothan
Wang, Kaijun
and
Wang, Yuling
2017.
Anti-Ramsey numbers for matchings in regular bipartite graphs.
Discrete Mathematics, Algorithms and Applications,
Vol. 09,
Issue. 02,
p.
1750019.
Jin, Zemin
and
Zang, Yuping
2017.
Anti-Ramsey coloring for matchings in complete bipartite graphs.
Journal of Combinatorial Optimization,
Vol. 33,
Issue. 1,
p.
1.
Jin, Zemin
Sun, Yuefang
Yan, Sherry H. F.
and
Zang, Yuping
2017.
Extremal coloring for the anti-Ramsey problem of matchings in complete graphs.
Journal of Combinatorial Optimization,
Vol. 34,
Issue. 4,
p.
1012.
Diao, Kefeng
Lu, Fuliang
Voloshin, Vitaly
and
Zhao, Ping
2017.
The Smallest Uniform Color-Bounded Hypergraphs Which are One-Realizations of a Given Set.
Graphs and Combinatorics,
Vol. 33,
Issue. 4,
p.
869.
Gorgol, Izolda
2017.
Avoiding rainbow 2-connected subgraphs.
Open Mathematics,
Vol. 15,
Issue. 1,
p.
393.
Jin, Zemin
2017.
Anti-Ramsey numbers for matchings in 3-regular bipartite graphs.
Applied Mathematics and Computation,
Vol. 292,
Issue. ,
p.
114.
Jin, Zemin
and
Ye, Kun
2018.
Rainbow number of matchings in planar graphs.
Discrete Mathematics,
Vol. 341,
Issue. 10,
p.
2846.
Jin, Zemin
Ye, Kecai
Sun, Yuefang
and
Chen, He
2018.
Rainbow matchings in edge-colored complete split graphs.
European Journal of Combinatorics,
Vol. 70,
Issue. ,
p.
297.
Jia, Yuxing
Lu, Mei
and
Zhang, Yi
2019.
Anti-Ramsey Problems in Complete Bipartite Graphs for t Edge-Disjoint Rainbow Spanning Subgraphs: Cycles and Matchings.
Graphs and Combinatorics,
Vol. 35,
Issue. 5,
p.
1011.
Qin, Zhongmei
Lan, Yongxin
and
Shi, Yongtang
2019.
Improved bounds for rainbow numbers of matchings in plane triangulations.
Discrete Mathematics,
Vol. 342,
Issue. 1,
p.
221.
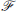 of graphs, let
of graphs, let 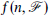 denote the maximum number of colours in an edge-colouring of
denote the maximum number of colours in an edge-colouring of 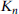 such that no subgraph of
such that no subgraph of 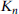 belonging to
belonging to 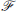 has distinct colours on its edges. Erdös, Simonovits and Sós [6] conjectured for fixed k with
has distinct colours on its edges. Erdös, Simonovits and Sós [6] conjectured for fixed k with 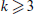 that
that 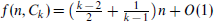 . This has been proved for
. This has been proved for 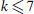 . For general k, in this paper we improve the previous bound of
. For general k, in this paper we improve the previous bound of 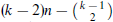 to
to 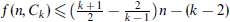 . For even k, we further improve it to
. For even k, we further improve it to 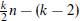 . We also prove that
. We also prove that 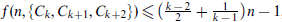 , which is sharp.
, which is sharp.

