Published online by Cambridge University Press: 04 February 2014
We present a two-parameter family 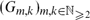 $(G_{m,k})_{m, k \in \mathbb{N}_{\geq 2}}$, of finite, non-abelian random groups and propose that, for each fixed k, as m → ∞ the commuting graph of Gm,k is almost surely connected and of diameter k. We present heuristic arguments in favour of this conjecture, following the lines of classical arguments for the Erdős–Rényi random graph. As well as being of independent interest, our groups would, if our conjecture is true, provide a large family of counterexamples to the conjecture of Iranmanesh and Jafarzadeh that the commuting graph of a finite group, if connected, must have a bounded diameter. Simulations of our model yielded explicit examples of groups whose commuting graphs have all diameters from 2 up to 10.
$(G_{m,k})_{m, k \in \mathbb{N}_{\geq 2}}$, of finite, non-abelian random groups and propose that, for each fixed k, as m → ∞ the commuting graph of Gm,k is almost surely connected and of diameter k. We present heuristic arguments in favour of this conjecture, following the lines of classical arguments for the Erdős–Rényi random graph. As well as being of independent interest, our groups would, if our conjecture is true, provide a large family of counterexamples to the conjecture of Iranmanesh and Jafarzadeh that the commuting graph of a finite group, if connected, must have a bounded diameter. Simulations of our model yielded explicit examples of groups whose commuting graphs have all diameters from 2 up to 10.