Published online by Cambridge University Press: 06 March 2015
Let 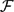 $\mathcal{F}$ be a family of r-uniform hypergraphs. The chromatic threshold of
$\mathcal{F}$ be a family of r-uniform hypergraphs. The chromatic threshold of 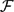 $\mathcal{F}$ is the infimum of all non-negative reals c such that the subfamily of
$\mathcal{F}$ is the infimum of all non-negative reals c such that the subfamily of 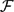 $\mathcal{F}$ comprising hypergraphs H with minimum degree at least
$\mathcal{F}$ comprising hypergraphs H with minimum degree at least 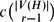 $c \binom{| V(H) |}{r-1}$ has bounded chromatic number. This parameter has a long history for graphs (r = 2), and in this paper we begin its systematic study for hypergraphs.
$c \binom{| V(H) |}{r-1}$ has bounded chromatic number. This parameter has a long history for graphs (r = 2), and in this paper we begin its systematic study for hypergraphs.
Łuczak and Thomassé recently proved that the chromatic threshold of the so-called near bipartite graphs is zero, and our main contribution is to generalize this result to r-uniform hypergraphs. For this class of hypergraphs, we also show that the exact Turán number is achieved uniquely by the complete (r + 1)-partite hypergraph with nearly equal part sizes. This is one of very few infinite families of non-degenerate hypergraphs whose Turán number is determined exactly. In an attempt to generalize Thomassen's result that the chromatic threshold of triangle-free graphs is 1/3, we prove bounds for the chromatic threshold of the family of 3-uniform hypergraphs not containing {abc, abd, cde}, the so-called generalized triangle.
In order to prove upper bounds we introduce the concept of fibre bundles, which can be thought of as a hypergraph analogue of directed graphs. This leads to the notion of fibre bundle dimension, a structural property of fibre bundles that is based on the idea of Vapnik–Chervonenkis dimension in hypergraphs. Our lower bounds follow from explicit constructions, many of which use a hypergraph analogue of the Kneser graph. Using methods from extremal set theory, we prove that these Kneser hypergraphs have unbounded chromatic number. This generalizes a result of Szemerédi for graphs and might be of independent interest. Many open problems remain.