Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T21:52:24.210Z Has data issue: false hasContentIssue false
  • English
  • Français

On Ramsey Numbers of Sparse Graphs

Published online by Cambridge University Press:  03 December 2003

Alexander Kostochka  and
B Sudakov
Alexander Kostochka*
Affiliation:
University of Illinois, Urbana, IL 61801, USA and Institute of Mathematics, Novosibirsk, 630090, Russia
B Sudakov*
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ 08540, USA and Institute for Advanced Study, Princeton, NJ 08540, USA
*
(e-mail: [email protected])
(e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The Ramsey number, 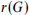, of a graph G is the minimum integer N such that, in every 2-colouring of the edges of the complete graph 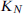on N vertices, there is a monochromatic copy of G. In 1975, Burr and Erdős posed a problem on Ramsey numbers of d-degenerate graphs, i.e., graphs in which every subgraph has a vertex of degree at most d. They conjectured that for every d there exists a constant c(d) such that for any d-degenerate graph G of order n.

In this paper we prove that 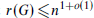for each such G. In fact, we show that, for every , sufficiently large n, and any graph H of order 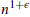, either H or its complement contains a (d,n)-common graph, that is, a graph in which every set of d vertices has at least n common neighbours. It is easy to see that any (d,n)-common graph contains every d-degenerate graph G of order n. We further show that, for every constant C, there is an n and a graph H of order 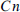such that neither H nor its complement contains a 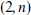-common graph.

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 12 , Issue 5-6: This issue contains volume twelve, parts five and six , November 2003 , pp. 627 - 641
Copyright
Copyright © Cambridge University Press 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Partially supported by NSF grant DMS-0099608 and the Dutch–Russian grant NWO-047-008-006.

‡

Partially supported by NSF grants DMS-0106589, CCR-9987845 and by the State of New Jersey.