Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-30T20:13:43.394Z Has data issue: false hasContentIssue false
  • English
  • Français

On Even-Degree Subgraphs of Linear Hypergraphs

Published online by Cambridge University Press:  02 February 2012

D. DELLAMONICA Jr. ,
P. HAXELL ,
T. ŁUCZAK ,
D. MUBAYI ,
B. NAGLE ,
Y. PERSON ,
V. RÖDL ,
M. SCHACHT  and
J. VERSTRAËTE
D. DELLAMONICA Jr.
Affiliation:
Department of Mathematics and Computer Science, Emory University, Atlanta, GA 30322, USA (e-mail: [email protected], [email protected])
P. HAXELL
Affiliation:
Department of Combinatorics and Optimization, University of Waterloo, Waterloo, ON N2L 3G1, Canada (e-mail: [email protected])
T. ŁUCZAK
Affiliation:
Department of Mathematics and Computer Science, Emory University, Atlanta, GA 30322, USA (e-mail: [email protected], [email protected]) Department of Discrete Mathematics, Faculty of Mathematics and Computer Science, Adam Mickiewicz University, Umultowska 87, 61-614 Poznań, Poland (e-mail: [email protected])
D. MUBAYI
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois, Chicago, IL 60607, USA (e-mail: [email protected])
B. NAGLE
Affiliation:
Department of Mathematics and Statistics, University of South Florida, Tampa, FL 33620, USA (e-mail: [email protected])
Y. PERSON
Affiliation:
Institute of Mathematics, Freie Universität Berlin, 14195 Berlin, Germany (e-mail: [email protected])
V. RÖDL
Affiliation:
Department of Mathematics and Computer Science, Emory University, Atlanta, GA 30322, USA (e-mail: [email protected], [email protected])
M. SCHACHT
Affiliation:
Fachbereich Mathematik, Universität Hamburg, Bundesstraße 55, D-20146 Hamburg, Germany (e-mail: [email protected])
J. VERSTRAËTE
Affiliation:
Department of Mathematics, University of California, San Diego (UCSD), La Jolla, CA 92093-0112, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A subgraph of a hypergraph H is even if all its degrees are positive even integers, and b-bounded if it has maximum degree at most b. Let fb(n) denote the maximum number of edges in a linearn-vertex 3-uniform hypergraph which does not contain a b-bounded even subgraph. In this paper, we show that if b ≥ 12, then 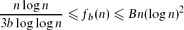for some absolute constant B, thus establishing fb(n) up to polylogarithmic factors. This leaves open the interesting case b = 2, which is the case of 2-regular subgraphs. We are able to show for some constants c, C > 0 that 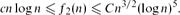We conjecture that f2(n) = n1 + o(1) as n → ∞.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 1-2: Honouring the Memory of Richard H. Schelp , March 2012 , pp. 113 - 127
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N., Friedland, S. and Kalai, G. (1984) Regular subgraphs of almost regular graphs. J. Combin. Theory Ser. B 37 79–91.CrossRefGoogle Scholar
[2]Feige, U. (2008) Small linear dependencies for binary vectors of low weight. In Building Bridges: Between Mathematics and Computer Science, Vol. 19 of Bolyai Society Mathematical Studies, Springer, pp. 283–307.CrossRefGoogle Scholar
[3]Frankl, P. and Rödl, V. (1985) Near perfect coverings in graphs and hypergraphs. European J. Combin. 6 317–326.CrossRefGoogle Scholar
[4]Lazebnik, F. and Ustimenko, V. A. (1995) Explicit construction of graphs with an arbitrary large girth and of large size. Discrete Appl. Math. 60 275–284.CrossRefGoogle Scholar
[5]Lovász, L. Personal communication.Google Scholar
[6]Mubayi, D. and Verstraëte, J. (2009) Two-regular subgraphs of hypergraphs. J. Combin. Theory Ser. B 99 643–655.CrossRefGoogle Scholar
[7]Naor, A. and Verstraëte, J. (2008) Parity check matrices and product representations of squares. Combinatorica 28 163–185.CrossRefGoogle Scholar
[8]Pyber, L., Rödl, V. and Szemerédi, E. (1995) Dense graphs without 3-regular subgraphs. J. Combin. Theory Ser. B 63 41–54.CrossRefGoogle Scholar