Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-15T18:05:27.104Z Has data issue: false hasContentIssue false
  • English
  • Français

Monochromatic paths and cycles in 2-edge-coloured graphs with large minimum degree

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  14 June 2021

József Balogh ,
Alexandr Kostochka ,
Mikhail Lavrov  and
Xujun Liu
József Balogh
Affiliation:
Department of Mathematics, University of Illinois, Urbana–Champaign, IL61801, USA Moscow Institute of Physics and Technology, Dolgoprudny, Russian Federation
Alexandr Kostochka
Affiliation:
Department of Mathematics, University of Illinois, Urbana–Champaign, IL61801, USA Sobolev Institute of Mathematics, Novosibirsk630090, Russia
Mikhail Lavrov
Affiliation:
Department of Mathematics, Kennesaw State University, Marietta, GA30060, USA
Xujun Liu*
Affiliation:
Coordinated Science Laboratory, University of Illinois, Urbana–Champaign, IL61801, USA
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

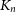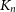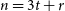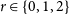A graph G arrows a graph H if in every 2-edge-colouring of G there exists a monochromatic copy of H. Schelp had the idea that if the complete graph $K_n$ arrows a small graph H, then every ‘dense’ subgraph of $K_n$ also arrows H, and he outlined some problems in this direction. Our main result is in this spirit. We prove that for every sufficiently large n, if $n = 3t+r$ where $r \in \{0,1,2\}$ and G is an n-vertex graph with 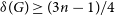$\delta(G) \ge (3n-1)/4$ , then for every 2-edge-colouring of G, either there are cycles of every length 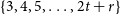$\{3, 4, 5, \dots, 2t+r\}$ of the same colour, or there are cycles of every even length 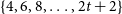$\{4, 6, 8, \dots, 2t+2\}$ of the samecolour.

Our result is tight in the sense that no longer cycles (of length 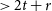$>2t+r$ ) can be guaranteed and the minimum degree condition cannot be reduced. It also implies the conjecture of Schelp that for every sufficiently large n, every 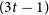$(3t-1)$ -vertex graph G with minimum degree larger than 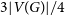$3|V(G)|/4$ arrows the path 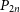$P_{2n}$ with 2n vertices. 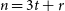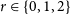Moreover, it implies for sufficiently large n the conjecture by Benevides, Łuczak, Scott, Skokan and White that for $n=3t+r$ where $r \in \{0,1,2\}$ and every n-vertex graph G with 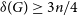$\delta(G) \ge 3n/4$ , in each 2-edge-colouring of G there exists a monochromatic cycle of length at least 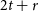$2t+r$ .

Keywords

Ramsey numberRegularity Lemmapaths and cycles

MSC classification

Primary: 05C55: Generalized Ramsey theory
Secondary: 05C35: Extremal problems 05C38: Paths and cycles 05D10: Ramsey theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 1 , January 2022 , pp. 109 - 122
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research of this author is partially supported by NSF Grant DMS-1764123, Arnold O. Beckman Research Award (UIUC) Campus Research Board 18132 and the Langan Scholar Fund (UIUC).

‡

Research of this author is supported in part by NSF grant DMS-1600592, Arnold O. Beckman Research Award (UIUC) RB20003 and by grants 18-01-00353 and 19-01-00682 of the Russian Foundation for Basic Research.

§

The work was partially done while M. Lavrov was a postdoc at Department of Mathematics, University of Illinois at Urbanaâ–Champaign.

The work was partially done while X. Liu was a PhD student at Department of Mathematics, University of Illinois at Urbana–Champaign. Research of this author was supported by the Waldemar J., Barbara G., and Juliette Alexandra Trjitzinsky Fellowship.

Dedicated to the memory of Richard H. Schelp

References

Bagga, K. and Varma, B. (1991) Bipartite graphs and degree conditions. In Graph Theory, Combinatorics, Algorithms and Applications, Proceedings of the 2nd International Conference, San Francisco, CA, 1989, pp. 564–573.Google Scholar
Balogh, J., Kostochka, A., Lavrov, M. and Liu, X. (2020) Long monochromatic paths and cycles in 2-edge-colored multipartite graphs. Moscow J. Comb. Number Theory 9(1) 55–100.Google Scholar
Benevides, F. S., Łuczak, T., Scott, A., Skokan, J. and White, M. (2012) Monochromatic cycles in 2-coloured graphs. Combin. Probab. Comput. 21(1–2) 57–87.CrossRefGoogle Scholar
Berge, C. (1976) Graphs and Hypergraphs. Translated from the French by Edward Minieka. Second revised edition. North-Holland Mathematical Library, Vol. 6, North-Holland Publishing Co., Amsterdam-London; American Elsevier Publishing Co., Inc., New York, pp. ix+528.Google Scholar
Bondy, J. (1971) Pancyclic graphs I. J. Combin. Theory 11 80–84.CrossRefGoogle Scholar
Bondy, J. and Simonovits, M. (1974) Cycles of even length in graphs. J. Combin. Theory B 16 97–105.CrossRefGoogle Scholar
Chvátal, V. (1972) On Hamilton’s ideals. J. Combin. Theory B 12 163–168.CrossRefGoogle Scholar
Figaj, A. and Łuczak, T. (2007) The Ramsey number for a triple of long even cycles. J. Combin. Theory B 97 584–596.CrossRefGoogle Scholar
Gerencsér, L. and Gyárfás, A. (1967) On Ramsey-type problems. Ann. Sci. Budapest. Eötvös Sect. Math. 10 167–170.Google Scholar
Gyárfás, A. and Lehel, J. (1973) A Ramsey type problem in directed and bipartite graphs. Periodica Math. Hung. 3 261–270.CrossRefGoogle Scholar
Gyárfás, A., Ruszinkó, M., Sárközy, G. N. and Szemerédi, E. (2007) Tripartite Ramsey numbers for paths. J. Graph Theory 55 164–174.CrossRefGoogle Scholar
Gyárfás, A. and Sárközy, G. N. (2012) Star versus two stripes Ramsey numbers and a conjecture of Schelp. Combin. Probab. Comput. 21(1–2) 179–186.CrossRefGoogle Scholar
Jackson, B. (1981) Cycles in bipartite graphs. J. Combin. Theory B 30(3), 332–342.CrossRefGoogle Scholar
Komlós, J., Sárközy, G. N. and Szemerédi, E. (1997) Blow-up lemma. Combinatorica 17 109–123.CrossRefGoogle Scholar
Li, H., Nikiforov, V. and Schelp, R. H. (2010) A new type of Ramsey–Turán problems. Discrete Math. 272 187–196.Google Scholar
Łuczak, T. (1999) $R(C_n,C_n,C_n)\leq (4+o(1))n$ . J. Combin. Theory B 75 174–187.CrossRefGoogle Scholar
Schelp, R. H. (2012) Some Ramsey–Turán type problems and related questions. Discrete Math. 312(14) 2158–2161.CrossRefGoogle Scholar
Szemerédi, E. (1978) Regular partitions of graphs. Problèmes combinatoires et théorie des graphes (Colloq. Internat. CNRS, Univ. Orsay, Orsay, 1976), pp. 399–401, Colloq. Internat. CNRS, 260, CNRS, Paris.Google Scholar
White, M. (2017) The monochromatic circumference of 2-edge-coloured graphs. J. Graph Theory 85 133–151.CrossRefGoogle Scholar