Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T18:00:13.721Z Has data issue: false hasContentIssue false
  • English
  • Français

Large Deviations and Ratio Limit Theorems for Pattern-Avoiding Permutations

Published online by Cambridge University Press:  13 December 2013

MAHSHID ATAPOUR  and
NEAL MADRAS
MAHSHID ATAPOUR
Affiliation:
Department of Finance and Management Science, University of Saskatchewan, 25 Campus Drive, Saskatoon, Saskatchewan S7N 5A7, Canada (e-mail: [email protected])
NEAL MADRAS
Affiliation:
Department of Mathematics and Statistics, York University, 4700 Keele Street, Toronto, Ontario M3J 1P3, Canada (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For a fixed permutation τ, let 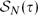$\mathcal{S}_N(\tau)$ be the set of permutations on N elements that avoid the pattern τ. Madras and Liu (2010) conjectured that 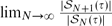$\lim_{N\rightarrow\infty}\frac{|\mathcal{S}_{N+1}(\tau)|}{ |\mathcal{S}_N(\tau)|}$ exists; if it does, it must equal the Stanley–Wilf limit. We prove the conjecture for every permutation τ of length 5 or less, as well as for some longer cases (including 704 of the 720 permutations of length 6). We also consider permutations drawn at random from 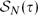$\mathcal{S}_N(\tau)$, and we investigate properties of their graphs (viewing permutations as functions on {1,. . .,N}) scaled down to the unit square [0,1]2. We prove exact large deviation results for these graphs when τ has length 3; it follows, for example, that it is exponentially unlikely for a random 312-avoiding permutation to have points above the diagonal strip |y−x| < ε, but not unlikely to have points below the strip. For general τ, we show that some neighbourhood of the upper left corner of [0,1]2 is exponentially unlikely to contain a point of the graph if and only if τ starts with its largest element. For patterns such as τ=4231 we establish that this neighbourhood can be extended along the sides of [0,1]2 to come arbitrarily close to the corner points (0,0) and (1,1), as simulations had suggested.

Keywords

Primary 60C05Secondary 05A0505A1660F10
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 2 , March 2014 , pp. 161 - 200
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Albert, M. H., Elder, M., Rechnitzer, A., Westcott, P. and Zabrocki, M. (2006) On the Stanley–Wilf limit of 4231-avoiding permutations and a conjecture of Arratia. Adv. Appl. Math. 36 96–105.CrossRefGoogle Scholar
[2]Alon, N. and Friedgut, E. (2000) On the number of permutations avoiding a given pattern. J. Combin. Theory Ser. A 89 133–140.CrossRefGoogle Scholar
[3]Arratia, R. (1999) On the Stanley–Wilf conjecture for the number of permutations avoiding a given pattern. Electron. J. Combin. 6 N1.Google Scholar
[4]Atkinson, M. D. and Stitt, T. (2002) Restricted permutations and the wreath product. Discrete Math. 259 19–36.CrossRefGoogle Scholar
[5]Backelin, J., West, J. and Xin, G. (2001) Wilf equivalence for singleton classes. In Proc. 13th Conference on Formal Power Series and Algebraic Combinatorics, Tempe, AZ, 2001.Google Scholar
[6]Bóna, M. (1999) The solution of a conjecture of Stanley and Wilf for all layered patterns. J. Combin. Theory Ser. A 85 96–104.CrossRefGoogle Scholar
[7]Bóna, M. (2004) Combinatorics of Permutations, Chapman & Hall/CRC.Google Scholar
[8]Bóna, M. (2007) New records in Stanley–Wilf limits. Europ. J. Combin. 28 75–85.Google Scholar
[9]Bóna, M. A new upper bound for 1324-avoiding permutations. Preprint. arXiv:1207.2379Google Scholar
[10]Bousquet-Mélou, M., Claesson, A., Dukes, M. and Kitaev, S. (2010) (2+2)-free posets, ascent sequences and pattern avoiding permutations. J. Combin. Theory Ser. A 117 884–909.CrossRefGoogle Scholar
[11]Claesson, A., Jelínek, V. and Steingrímsson, E. (2012) Upper bounds for the Stanley–Wilf limit of 1324 and other layered patterns. J. Combin. Theory Ser. A 119 1680–1691.Google Scholar
[12]Flajolet, P. and Sedgewick, R. (2009) Analytic Combinatorics, Cambridge University Press.Google Scholar
[13]Hammersley, J. M. and Whittington, S. G. (1985) Self-avoiding walks in wedges. J. Phys. A: Math. Gen. 18 101–111.Google Scholar
[14]Kesten, H. (1963) On the number of self-avoiding walks. J. Math. Phys. 4 960–969.Google Scholar
[15]Madras, N. and Liu, H. (2010) Random pattern-avoiding permutations. In Algorithmic Probability and Combinatorics (Lladser, M. E.et al., eds), Vol. 520 of Contemporary Mathematics, AMS.Google Scholar
[16]Madras, N. and Pehlivan, L. Structure of random 312-avoiding permutations. In preparation.Google Scholar
[17]Madras, N. and Slade, G. (1993) The Self-Avoiding Walk, Birkhäuser.Google Scholar
[18]Marcus, A. and Tardos, G. (2004) Excluded permutation matrices and the Stanley–Wilf conjecture. J. Combin. Theory Ser. A 107 153–160.Google Scholar
[19]Miner, S. and Pak, I. The shape of random pattern avoiding permutations. Preprint. arXiv:1303.7313Google Scholar
[20]Regev, A. (1981) Asymptotic values for degrees associated with strips of Young diagrams. Adv. Math. 41 115–136.Google Scholar
[21]Simon, R. and Schmidt, F. W. (1985) Restricted permutations. Europ. J. Combin. 6 383–406.Google Scholar