Hostname: page-component-f554764f5-nt87m Total loading time: 0 Render date: 2025-04-20T05:49:12.245Z Has data issue: false hasContentIssue false
  • English
  • Français

The Excluded Tree Minor Theorem Revisited

Published online by Cambridge University Press:  27 September 2023

Vida Dujmović ,
Robert Hickingbotham ,
Gwenaël Joret ,
Piotr Micek ,
Pat Morin  and
David R. Wood Open the ORCID record for David R. Wood [Opens in a new window]
Vida Dujmović
Affiliation:
School of Computer Science and Electrical Engineering, University of Ottawa, Ottawa, ON, Canada
Robert Hickingbotham
Affiliation:
School of Mathematics, Monash University, Melbourne, VIC, Australia
Gwenaël Joret
Affiliation:
Département d’Informatique, Université libre de Bruxelles, Bruxelles, Belgium
Piotr Micek*
Affiliation:
Faculty of Mathematics and Computer Science, Jagiellonian University, Kraków, Poland
Pat Morin
Affiliation:
School of Computer Science, Carleton University, Ottawa, ON, Canada
David R. Wood
Affiliation:
School of Mathematics, Monash University, Melbourne, VIC, Australia
*
Corresponding author: Piotr Micek; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

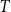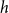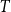We prove that for every tree $T$ of radius $h$, there is an integer $c$ such that every $T$-minor-free graph is contained in 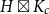$H\boxtimes K_c$ for some graph 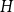$H$ with pathwidth at most 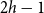$2h-1$. This is a qualitative strengthening of the Excluded Tree Minor Theorem of Robertson and Seymour (GM I). We show that radius is the right parameter to consider in this setting, and 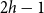$2h-1$ is the best possible bound.

Keywords

Structural graph theorypathwidthgraph minors
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 33 , Issue 1 , January 2024 , pp. 85 - 90
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

†

Vida Dujmović: Research supported by NSERC, and a Gordon Preston Fellowship from the School of Mathematics at Monash University.

‡

Robert Hickingbotham: Research supported by Australian Government Research Training Program Scholarships.

§

Gwenaël Joret: Supported by the Australian Research Council, and by a CDR grant and a PDR from the National Fund for Scientific Research (FNRS).

Pat Morin: Research supported by NSERC.

∥

David R. Wood: Research supported by the Australian Research Council.

References

Bienstock, D., Robertson, N., Seymour, P. and Thomas, R. (1991) Quickly excluding a forest. J. Comb. Theory Ser. B 52(2) 274–283.CrossRefGoogle Scholar
Campbell, R., Clinch, K., Distel, M., Gollin, J. P., Hendrey, K., Hickingbotham, R., Huynh, T., Illingworth, F., Tamitegama, Y., Tan, J. and Wood, D. R. (2022) Product structure of graph classes with bounded treewidth. arXiv: 2206.02395.Google Scholar
Diestel, R. (1995) Graph minors. I. A short proof of the path-width theorem. Comb. Probab. Comput. 4(1) 27–30.CrossRefGoogle Scholar
Diestel, R. (2018) Graph Theory, Vol. 173 of Graduate Texts in Mathematics, 5th edn. Springer.Google Scholar
Dujmović, V., Joret, G., Micek, P., Morin, P., Ueckerdt, T. and Wood, D. R. (2020) Planar graphs have bounded queue-number. J. ACM 67(4) 22.CrossRefGoogle Scholar
Illingworth, F., Scott, A. and Wood, D. R. (2022). Product structure of graphs with an excluded minor. arXiv: 2104.06627.Google Scholar
Norin, S., Scott, A., Seymour, P. and Wood, D. R. (2019) Clustered colouring in minor-closed classes. Combinatorica 39(6) 1387–1412.Google Scholar
Robertson, N. and Seymour, P. (1983) Graph minors. I. Excluding a forest. J. Comb. Theory Ser. B 35(1) 39–61.Google Scholar