Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Drmota, Michael
Giménez, Omer
and
Noy, Marc
2010.
Vertices of given degree in series‐parallel graphs.
Random Structures & Algorithms,
Vol. 36,
Issue. 3,
p.
273.
Feng, Qunqiang
and
Mahmoud, Hosam M.
2010.
On the Variety of Shapes on the Fringe of a Random Recursive Tree.
Journal of Applied Probability,
Vol. 47,
Issue. 01,
p.
191.
Feng, Qunqiang
and
Mahmoud, Hosam M.
2010.
On the Variety of Shapes on the Fringe of a Random Recursive Tree.
Journal of Applied Probability,
Vol. 47,
Issue. 1,
p.
191.
Li, Xueliang
and
Li, Yiyang
2011.
The asymptotic value of the Randić index for trees.
Advances in Applied Mathematics,
Vol. 47,
Issue. 2,
p.
365.
Gittenberger, Bernhard
and
Kraus, Veronika
2012.
The degree profile of random Pólya trees.
Journal of Combinatorial Theory, Series A,
Vol. 119,
Issue. 7,
p.
1528.
Li, Jing
and
Li, Yiyang
2015.
The asymptotic value of the zeroth-order Randić index and sum-connectivity index for trees.
Applied Mathematics and Computation,
Vol. 266,
Issue. ,
p.
1027.
Li, Xueliang
Li, Yiyang
and
Shi, Yongtang
2016.
The asymptotic number of non-isomorphic rooted trees obtained by rooting a tree.
Journal of Mathematical Analysis and Applications,
Vol. 434,
Issue. 1,
p.
1.
Cai, Xing Shi
and
Luc, Devroye
2017.
A study of large fringe and non-fringe subtrees
in conditional Galton-Watson trees
.
Latin American Journal of Probability and Mathematical Statistics,
Vol. 14,
Issue. 1,
p.
579.
Drmota, Michael
Ramos, Lander
and
Rué, Juanjo
2017.
Subgraph statistics in subcritical graph classes.
Random Structures & Algorithms,
Vol. 51,
Issue. 4,
p.
631.
Janson, Svante
2021.
On general subtrees of a conditioned Galton–Watson tree.
Electronic Communications in Probability,
Vol. 26,
Issue. none,
Koechlin, Florent
Nicaud, Cyril
and
Rotondo, Pablo
2021.
Simplifications of Uniform Expressions Specified by Systems.
International Journal of Foundations of Computer Science,
Vol. 32,
Issue. 06,
p.
733.
Isaev, Mikhail
Southwell, Angus
and
Zhukovskii, Maksim
2022.
Distribution of tree parameters by martingale approach.
Combinatorics, Probability and Computing,
Vol. 31,
Issue. 5,
p.
737.


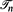 denote the set of unrooted labelled trees of size
denote the set of unrooted labelled trees of size 