Article contents
Counting Hamilton cycles in Dirac hypergraphs
Published online by Cambridge University Press: 17 December 2020
Abstract
A tight Hamilton cycle in a k-uniform hypergraph (k-graph) G is a cyclic ordering of the vertices of G such that every set of k consecutive vertices in the ordering forms an edge. Rödl, Ruciński and Szemerédi proved that for 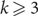 $k\ge 3$
, every k-graph on n vertices with minimum codegree at least
$k\ge 3$
, every k-graph on n vertices with minimum codegree at least  $n/2+o(n)$
contains a tight Hamilton cycle. We show that the number of tight Hamilton cycles in such k-graphs is
$n/2+o(n)$
contains a tight Hamilton cycle. We show that the number of tight Hamilton cycles in such k-graphs is 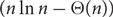 ${\exp(n\ln n-\Theta(n))}$
. As a corollary, we obtain a similar estimate on the number of Hamilton
${\exp(n\ln n-\Theta(n))}$
. As a corollary, we obtain a similar estimate on the number of Hamilton 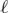 ${\ell}$
-cycles in such k-graphs for all
${\ell}$
-cycles in such k-graphs for all 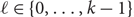 ${\ell\in\{0,\ldots,k-1\}}$
, which makes progress on a question of Ferber, Krivelevich and Sudakov.
${\ell\in\{0,\ldots,k-1\}}$
, which makes progress on a question of Ferber, Krivelevich and Sudakov.
MSC classification
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
Footnotes
This project has received partial funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement 786198, D. Kühn and D. Osthus). The research leading to these results was also partially supported by the EPSRC, grants EP/N019504/1 (S. Glock and D. Kühn) and EP/S00100X/1 (D. Osthus), and the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), grants 339933727 and 428212407 (F. Joos), as well as the Royal Society and the Wolfson Foundation (D. Kühn).
References
- 4
- Cited by



